Addressing pitfalls in implicit unobserved confounding synthesis using explicit block hierarchical ancestral sampling

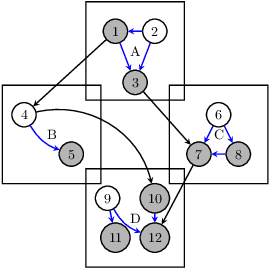
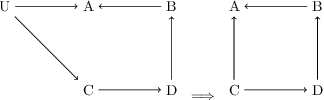
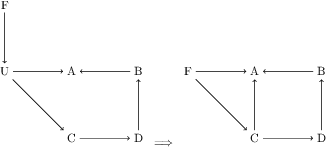
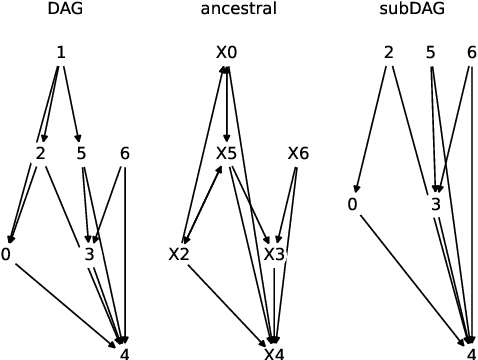
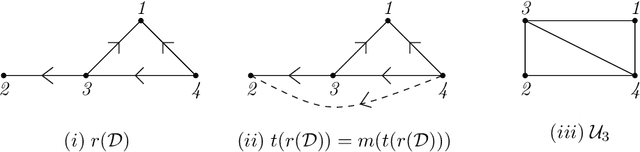
Unbiased data synthesis is crucial for evaluating causal discovery algorithms in the presence of unobserved confounding, given the scarcity of real-world datasets. A common approach, implicit parameterization, encodes unobserved confounding by modifying the off-diagonal entries of the idiosyncratic covariance matrix while preserving positive definiteness. Within this approach, state-of-the-art protocols have two distinct issues that hinder unbiased sampling from the complete space of causal models: first, the use of diagonally dominant constructions, which restrict the spectrum of partial correlation matrices; and second, the restriction of possible graphical structures when sampling bidirected edges, unnecessarily ruling out valid causal models. To address these limitations, we propose an improved explicit modeling approach for unobserved confounding, leveraging block-hierarchical ancestral generation of ground truth causal graphs. Algorithms for converting the ground truth DAG into ancestral graph is provided so that the output of causal discovery algorithms could be compared with. We prove that our approach fully covers the space of causal models, including those generated by the implicit parameterization, thus enabling more robust evaluation of methods for causal discovery and inference.

Scalable Structure Learning for Sparse Context-Specific Causal Systems

Several approaches to graphically representing context-specific relations among jointly distributed categorical variables have been proposed, along with structure learning algorithms. While existing optimization-based methods have limited scalability due to the large number of context-specific models, the constraint-based methods are more prone to error than even constraint-based DAG learning algorithms since more relations must be tested. We present a hybrid algorithm for learning context-specific models that scales to hundreds of variables while testing no more constraints than standard DAG learning algorithms. Scalable learning is achieved through a combination of an order-based MCMC algorithm and sparsity assumptions analogous to those typically invoked for DAG models. To implement the method, we solve a special case of an open problem recently posed by Alon and Balogh. The method is shown to perform well on synthetic data and real world examples, in terms of both accuracy and scalability.

Neuro-Causal Factor Analysis

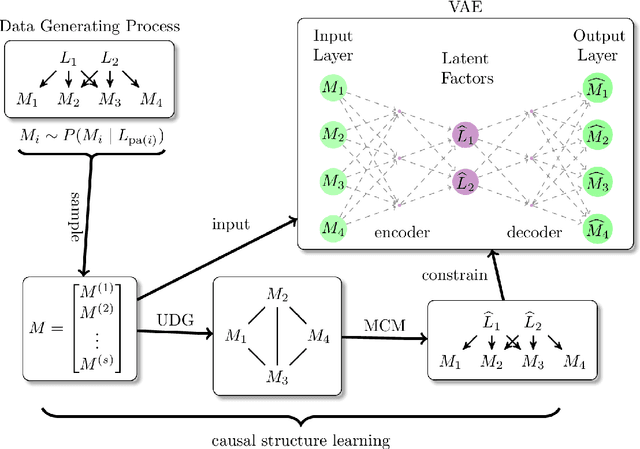
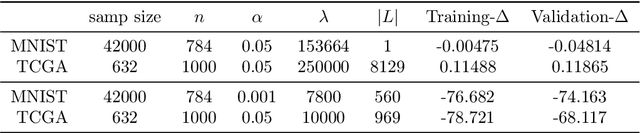
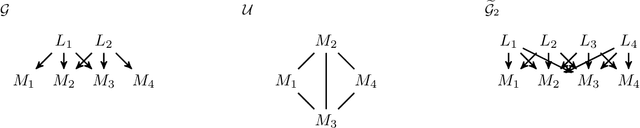
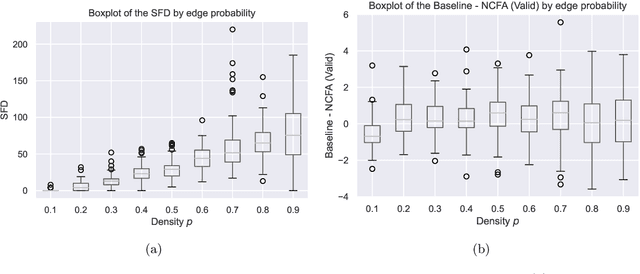
Factor analysis (FA) is a statistical tool for studying how observed variables with some mutual dependences can be expressed as functions of mutually independent unobserved factors, and it is widely applied throughout the psychological, biological, and physical sciences. We revisit this classic method from the comparatively new perspective given by advancements in causal discovery and deep learning, introducing a framework for Neuro-Causal Factor Analysis (NCFA). Our approach is fully nonparametric: it identifies factors via latent causal discovery methods and then uses a variational autoencoder (VAE) that is constrained to abide by the Markov factorization of the distribution with respect to the learned graph. We evaluate NCFA on real and synthetic data sets, finding that it performs comparably to standard VAEs on data reconstruction tasks but with the advantages of sparser architecture, lower model complexity, and causal interpretability. Unlike traditional FA methods, our proposed NCFA method allows learning and reasoning about the latent factors underlying observed data from a justifiably causal perspective, even when the relations between factors and measurements are highly nonlinear.

Queer In AI: A Case Study in Community-Led Participatory AI

We present Queer in AI as a case study for community-led participatory design in AI. We examine how participatory design and intersectional tenets started and shaped this community's programs over the years. We discuss different challenges that emerged in the process, look at ways this organization has fallen short of operationalizing participatory and intersectional principles, and then assess the organization's impact. Queer in AI provides important lessons and insights for practitioners and theorists of participatory methods broadly through its rejection of hierarchy in favor of decentralization, success at building aid and programs by and for the queer community, and effort to change actors and institutions outside of the queer community. Finally, we theorize how communities like Queer in AI contribute to the participatory design in AI more broadly by fostering cultures of participation in AI, welcoming and empowering marginalized participants, critiquing poor or exploitative participatory practices, and bringing participation to institutions outside of individual research projects. Queer in AI's work serves as a case study of grassroots activism and participatory methods within AI, demonstrating the potential of community-led participatory methods and intersectional praxis, while also providing challenges, case studies, and nuanced insights to researchers developing and using participatory methods.

Combinatorial and algebraic perspectives on the marginal independence structure of Bayesian networks

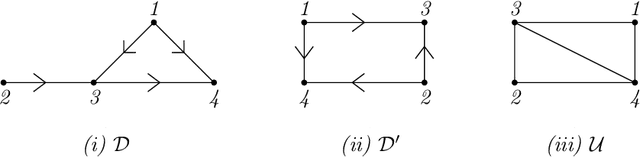
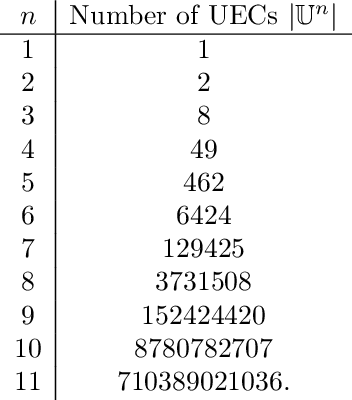
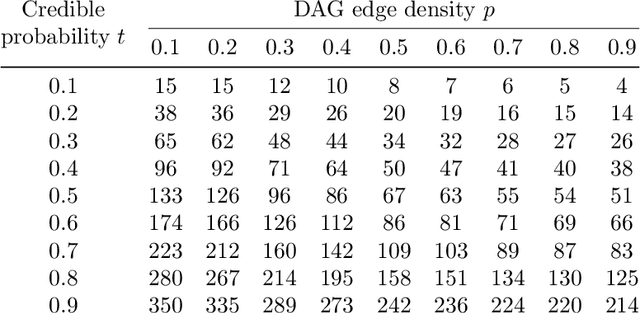
We consider the problem of estimating the marginal independence structure of a Bayesian network from observational data in the form of an undirected graph called the unconditional dependence graph. We show that unconditional dependence graphs correspond to the graphs having equal independence and intersection numbers. Using this observation, a Gr\"obner basis for a toric ideal associated to unconditional dependence graphs is given and then extended by additional binomial relations to connect the space of unconditional dependence graphs. An MCMC method, called GrUES (Gr\"obner-based Unconditional Equivalence Search), is implemented based on the resulting moves and applied to synthetic Gaussian data. GrUES recovers the true marginal independence structure via a BIC-optimal or MAP estimate at a higher rate than simple independence tests while also yielding an estimate of the posterior, for which the $20\%$ HPD credible sets include the true structure at a high rate for graphs with density at least $0.5$.

Causal Structure Learning with Greedy Unconditional Equivalence Search

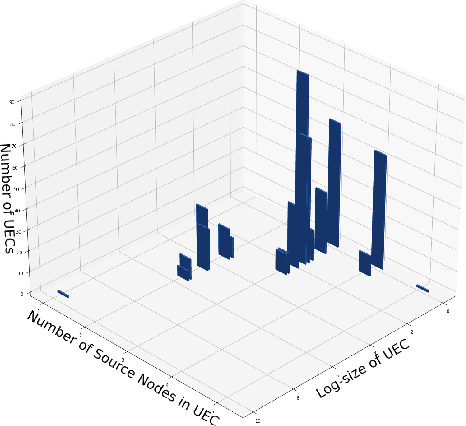
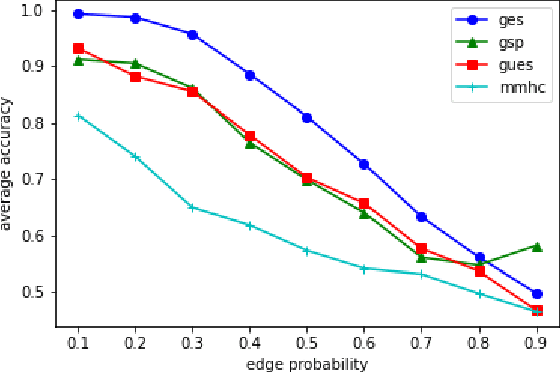
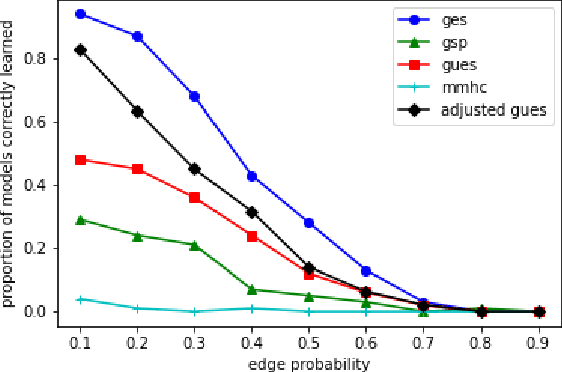
We consider the problem of characterizing directed acyclic graph (DAG) models up to unconditional equivalence, i.e., when two DAGs have the same set of unconditional d-separation statements. Each unconditional equivalence class (UEC) can be uniquely represented with an undirected graph whose clique structure encodes the members of the class. Via this structure, we provide a transformational characterization of unconditional equivalence. Combining these results, we introduce a hybrid algorithm for learning DAG models from observational data, called Greedy Unconditional Equivalence Search (GUES), which first estimates the UEC of the data using independence tests and then greedily searches the UEC for the optimal DAG. Applying GUES on synthetic data, we show that it achieves comparable accuracy to existing methods. However, in contrast to existing methods, since the average UEC is observed to contain few DAGs, the search space for GUES is drastically reduced.

A Distance Covariance-based Kernel for Nonlinear Causal Clustering in Heterogeneous Populations

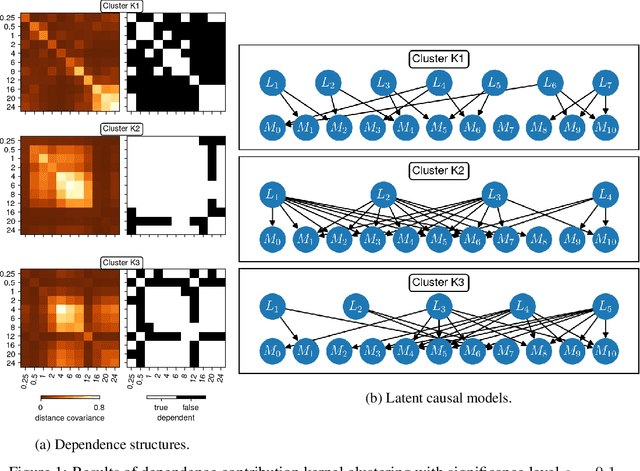
We consider the problem of causal structure learning in the setting of heterogeneous populations, i.e., populations in which a single causal structure does not adequately represent all population members, as is common in biological and social sciences. To this end, we introduce a distance covariance-based kernel designed specifically to measure the similarity between the underlying nonlinear causal structures of different samples. This kernel enables us to perform clustering to identify the homogeneous subpopulations. Indeed, we prove the corresponding feature map is a statistically consistent estimator of nonlinear independence structure, rendering the kernel itself a statistical test for the hypothesis that sets of samples come from different generating causal structures. We can then use existing methods to learn a causal structure for each of these subpopulations. We demonstrate using our kernel for causal clustering with an application in genetics, allowing us to reason about the latent transcription factor networks regulating measured gene expression levels.

Measurement Dependence Inducing Latent Causal Models

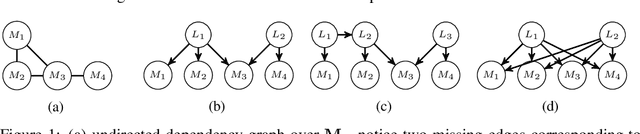
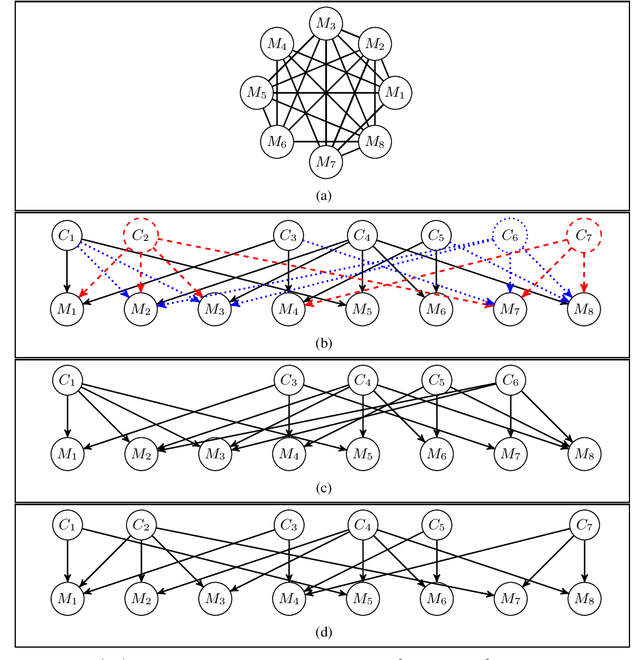
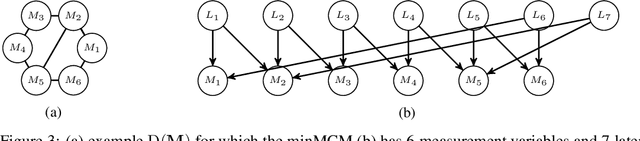
We consider the task of causal structure learning over measurement dependence inducing latent (MeDIL) causal models. We show that this task can be framed in terms of the graph theoretical problem of finding edge clique covers, resulting in a simple algorithm for returning minimal MeDIL causal models (minMCMs). This algorithm is non-parametric, requiring no assumptions about linearity or Gaussianity. Furthermore, despite rather weak assumptions about the class of MeDIL causal models, we show that minimality in minMCMs implies three rather specific and interesting properties: first, minMCMs provide lower bounds on (i) the number of latent causal variables and (ii) the number of functional causal relations that are required to model a complex system at any level of granularity; second, a minMCM contains no causal links between the latent variables; and third, in contrast to factor analysis, a minMCM may require more latent than measurement variables.