Neuro-Causal Factor Analysis
Paper and Code
May 31, 2023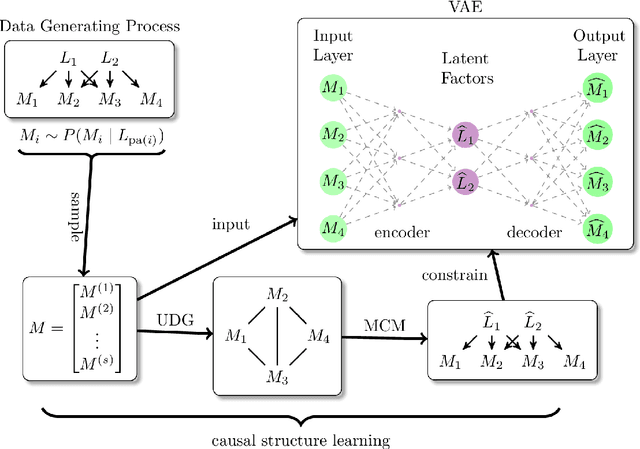
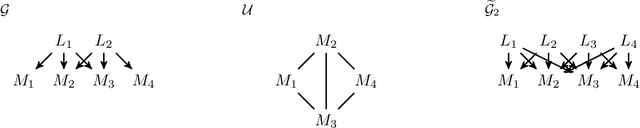
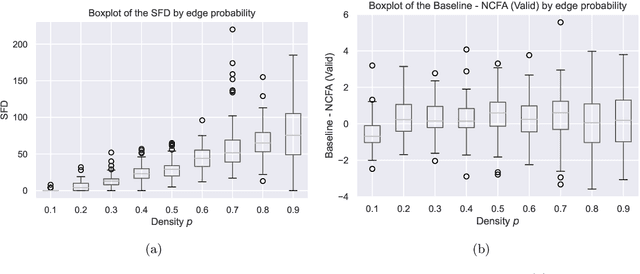
Factor analysis (FA) is a statistical tool for studying how observed variables with some mutual dependences can be expressed as functions of mutually independent unobserved factors, and it is widely applied throughout the psychological, biological, and physical sciences. We revisit this classic method from the comparatively new perspective given by advancements in causal discovery and deep learning, introducing a framework for Neuro-Causal Factor Analysis (NCFA). Our approach is fully nonparametric: it identifies factors via latent causal discovery methods and then uses a variational autoencoder (VAE) that is constrained to abide by the Markov factorization of the distribution with respect to the learned graph. We evaluate NCFA on real and synthetic data sets, finding that it performs comparably to standard VAEs on data reconstruction tasks but with the advantages of sparser architecture, lower model complexity, and causal interpretability. Unlike traditional FA methods, our proposed NCFA method allows learning and reasoning about the latent factors underlying observed data from a justifiably causal perspective, even when the relations between factors and measurements are highly nonlinear.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge