Scalable Structure Learning for Sparse Context-Specific Causal Systems

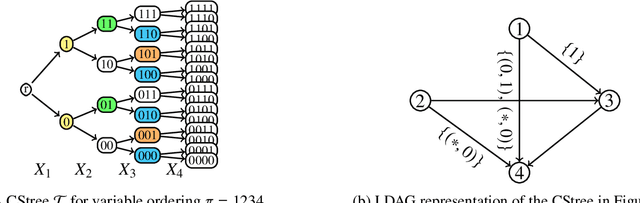
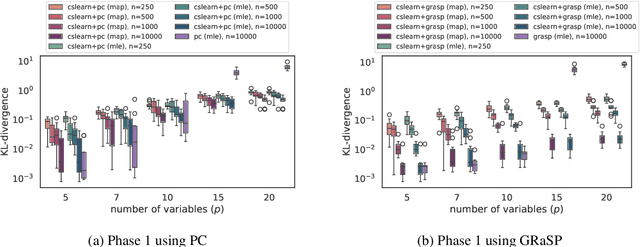
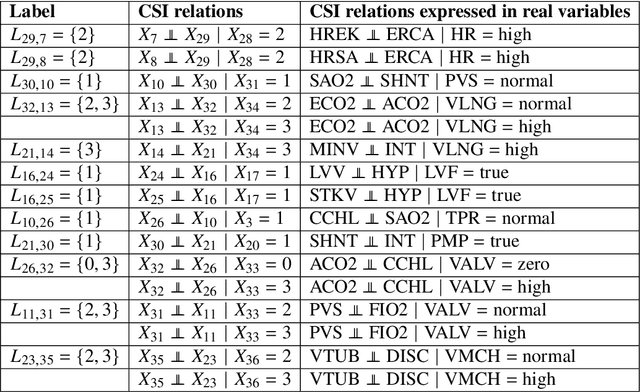
Several approaches to graphically representing context-specific relations among jointly distributed categorical variables have been proposed, along with structure learning algorithms. While existing optimization-based methods have limited scalability due to the large number of context-specific models, the constraint-based methods are more prone to error than even constraint-based DAG learning algorithms since more relations must be tested. We present a hybrid algorithm for learning context-specific models that scales to hundreds of variables while testing no more constraints than standard DAG learning algorithms. Scalable learning is achieved through a combination of an order-based MCMC algorithm and sparsity assumptions analogous to those typically invoked for DAG models. To implement the method, we solve a special case of an open problem recently posed by Alon and Balogh. The method is shown to perform well on synthetic data and real world examples, in terms of both accuracy and scalability.

Neuro-Causal Factor Analysis

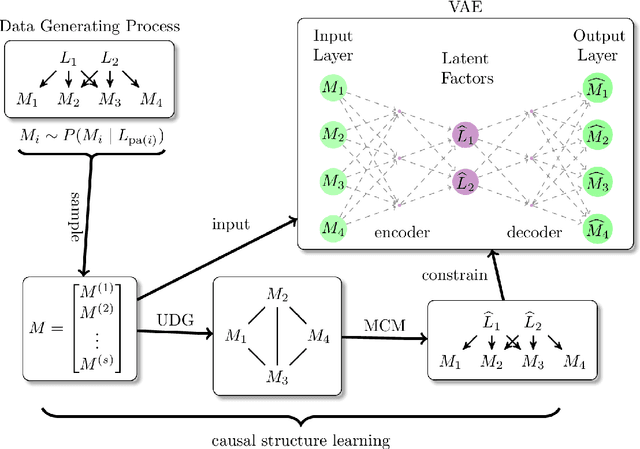
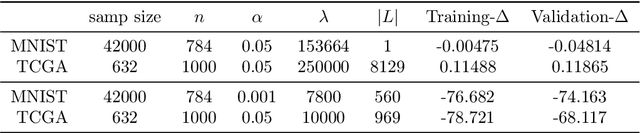
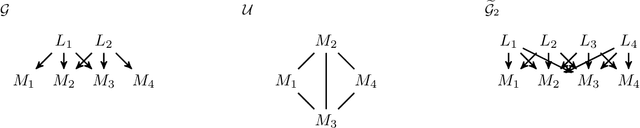
Factor analysis (FA) is a statistical tool for studying how observed variables with some mutual dependences can be expressed as functions of mutually independent unobserved factors, and it is widely applied throughout the psychological, biological, and physical sciences. We revisit this classic method from the comparatively new perspective given by advancements in causal discovery and deep learning, introducing a framework for Neuro-Causal Factor Analysis (NCFA). Our approach is fully nonparametric: it identifies factors via latent causal discovery methods and then uses a variational autoencoder (VAE) that is constrained to abide by the Markov factorization of the distribution with respect to the learned graph. We evaluate NCFA on real and synthetic data sets, finding that it performs comparably to standard VAEs on data reconstruction tasks but with the advantages of sparser architecture, lower model complexity, and causal interpretability. Unlike traditional FA methods, our proposed NCFA method allows learning and reasoning about the latent factors underlying observed data from a justifiably causal perspective, even when the relations between factors and measurements are highly nonlinear.

Combinatorial and algebraic perspectives on the marginal independence structure of Bayesian networks

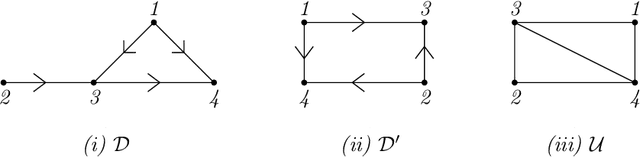
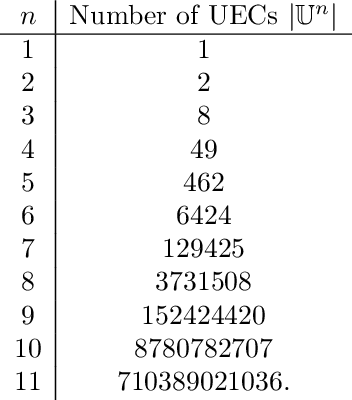
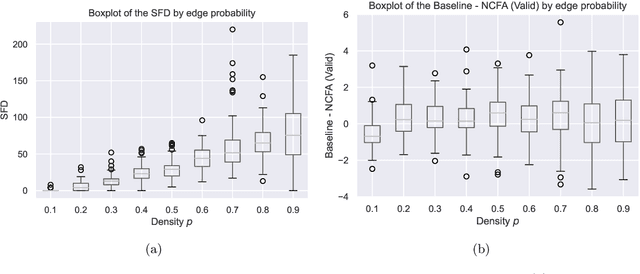
We consider the problem of estimating the marginal independence structure of a Bayesian network from observational data in the form of an undirected graph called the unconditional dependence graph. We show that unconditional dependence graphs correspond to the graphs having equal independence and intersection numbers. Using this observation, a Gr\"obner basis for a toric ideal associated to unconditional dependence graphs is given and then extended by additional binomial relations to connect the space of unconditional dependence graphs. An MCMC method, called GrUES (Gr\"obner-based Unconditional Equivalence Search), is implemented based on the resulting moves and applied to synthetic Gaussian data. GrUES recovers the true marginal independence structure via a BIC-optimal or MAP estimate at a higher rate than simple independence tests while also yielding an estimate of the posterior, for which the $20\%$ HPD credible sets include the true structure at a high rate for graphs with density at least $0.5$.

Causal Structure Learning with Greedy Unconditional Equivalence Search

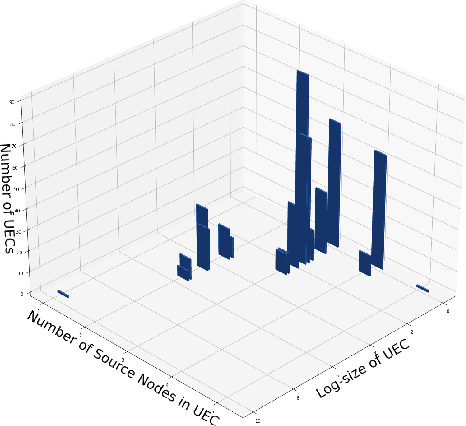
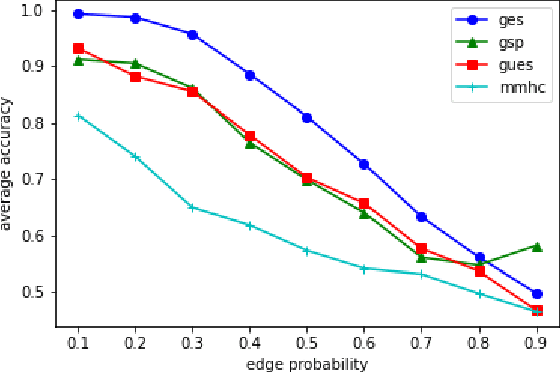
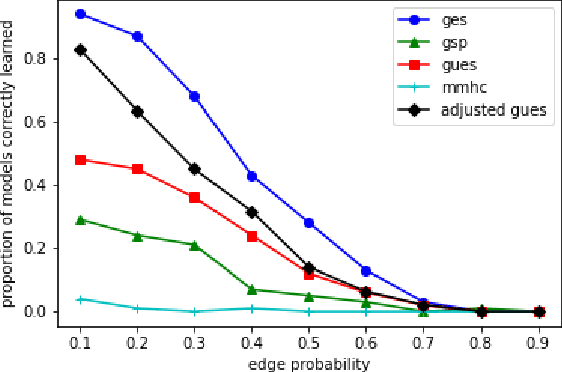
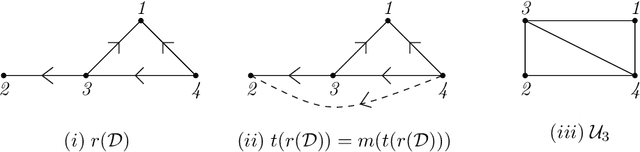
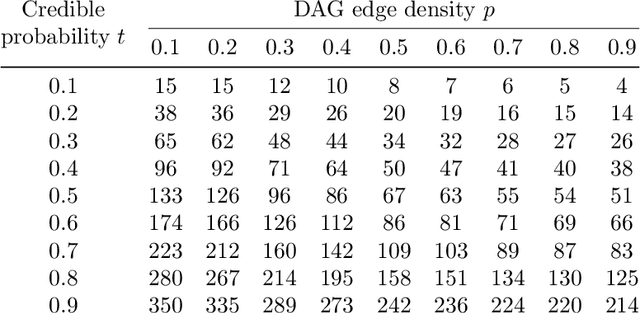
We consider the problem of characterizing directed acyclic graph (DAG) models up to unconditional equivalence, i.e., when two DAGs have the same set of unconditional d-separation statements. Each unconditional equivalence class (UEC) can be uniquely represented with an undirected graph whose clique structure encodes the members of the class. Via this structure, we provide a transformational characterization of unconditional equivalence. Combining these results, we introduce a hybrid algorithm for learning DAG models from observational data, called Greedy Unconditional Equivalence Search (GUES), which first estimates the UEC of the data using independence tests and then greedily searches the UEC for the optimal DAG. Applying GUES on synthetic data, we show that it achieves comparable accuracy to existing methods. However, in contrast to existing methods, since the average UEC is observed to contain few DAGs, the search space for GUES is drastically reduced.

Representation and Learning of Context-Specific Causal Models with Observational and Interventional Data

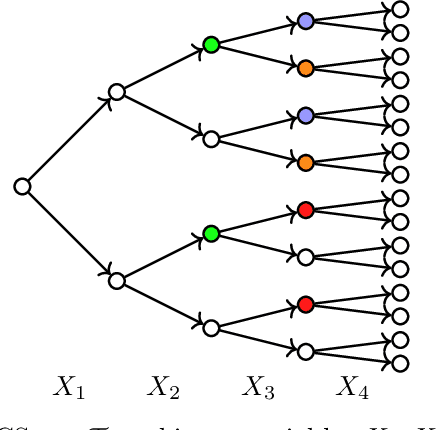
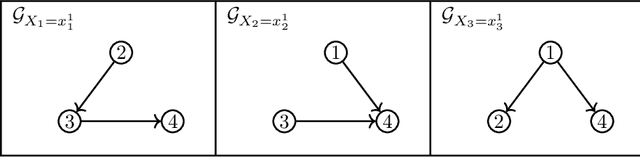
We consider the problem of representation and learning of causal models that encode context-specific information for discrete data. To represent such models we define the class of CStrees. This class is a subclass of staged tree models that captures context-specific information in a DAG model by the use of a staged tree, or equivalently, by a collection of DAGs. We provide a characterization of the complete set of asymmetric conditional independence relations encoded by a CStree that generalizes the global Markov property for DAGs. As a consequence, we obtain a graphical characterization of model equivalence for CStrees generalizing that of Verma and Pearl for DAG models. We also provide a closed-form formula for the maximum likelihood estimator of a CStree and use it to show that the Bayesian Information Criterion is a locally consistent score function for this model class. We then use the theory for general interventions in staged tree models to provide a global Markov property and a characterization of model equivalence for general interventions in CStrees. As examples, we apply these results to two real data sets, learning BIC-optimal CStrees for each and analyzing their context-specific causal structure.