Representation and Learning of Context-Specific Causal Models with Observational and Interventional Data
Paper and Code
Jan 22, 2021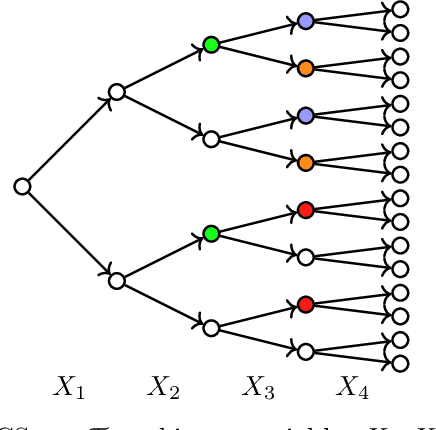
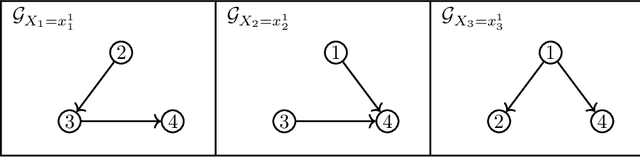


We consider the problem of representation and learning of causal models that encode context-specific information for discrete data. To represent such models we define the class of CStrees. This class is a subclass of staged tree models that captures context-specific information in a DAG model by the use of a staged tree, or equivalently, by a collection of DAGs. We provide a characterization of the complete set of asymmetric conditional independence relations encoded by a CStree that generalizes the global Markov property for DAGs. As a consequence, we obtain a graphical characterization of model equivalence for CStrees generalizing that of Verma and Pearl for DAG models. We also provide a closed-form formula for the maximum likelihood estimator of a CStree and use it to show that the Bayesian Information Criterion is a locally consistent score function for this model class. We then use the theory for general interventions in staged tree models to provide a global Markov property and a characterization of model equivalence for general interventions in CStrees. As examples, we apply these results to two real data sets, learning BIC-optimal CStrees for each and analyzing their context-specific causal structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge