Causal Structure Learning with Greedy Unconditional Equivalence Search

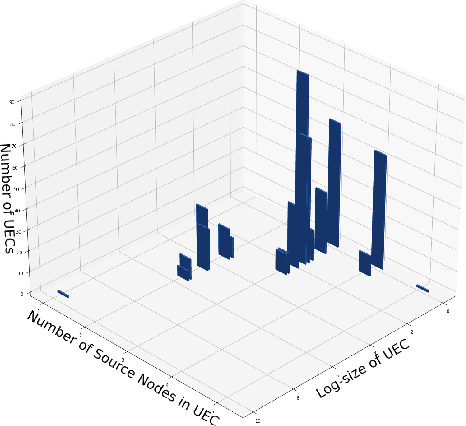
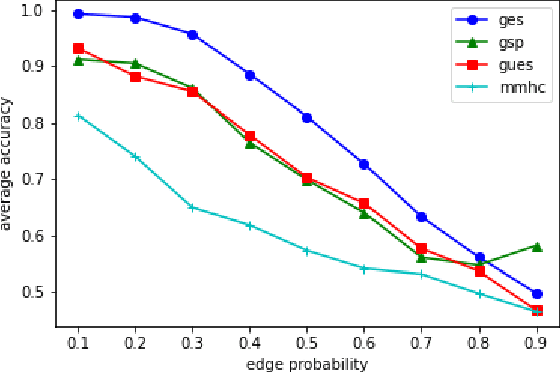
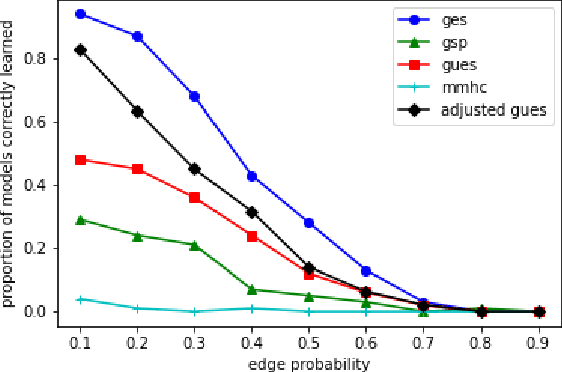
We consider the problem of characterizing directed acyclic graph (DAG) models up to unconditional equivalence, i.e., when two DAGs have the same set of unconditional d-separation statements. Each unconditional equivalence class (UEC) can be uniquely represented with an undirected graph whose clique structure encodes the members of the class. Via this structure, we provide a transformational characterization of unconditional equivalence. Combining these results, we introduce a hybrid algorithm for learning DAG models from observational data, called Greedy Unconditional Equivalence Search (GUES), which first estimates the UEC of the data using independence tests and then greedily searches the UEC for the optimal DAG. Applying GUES on synthetic data, we show that it achieves comparable accuracy to existing methods. However, in contrast to existing methods, since the average UEC is observed to contain few DAGs, the search space for GUES is drastically reduced.