Addressing pitfalls in implicit unobserved confounding synthesis using explicit block hierarchical ancestral sampling

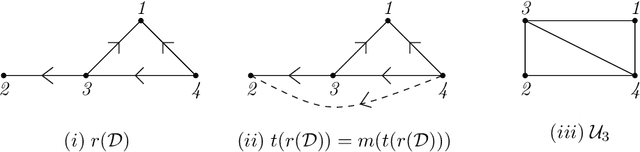
Unbiased data synthesis is crucial for evaluating causal discovery algorithms in the presence of unobserved confounding, given the scarcity of real-world datasets. A common approach, implicit parameterization, encodes unobserved confounding by modifying the off-diagonal entries of the idiosyncratic covariance matrix while preserving positive definiteness. Within this approach, state-of-the-art protocols have two distinct issues that hinder unbiased sampling from the complete space of causal models: first, the use of diagonally dominant constructions, which restrict the spectrum of partial correlation matrices; and second, the restriction of possible graphical structures when sampling bidirected edges, unnecessarily ruling out valid causal models. To address these limitations, we propose an improved explicit modeling approach for unobserved confounding, leveraging block-hierarchical ancestral generation of ground truth causal graphs. Algorithms for converting the ground truth DAG into ancestral graph is provided so that the output of causal discovery algorithms could be compared with. We prove that our approach fully covers the space of causal models, including those generated by the implicit parameterization, thus enabling more robust evaluation of methods for causal discovery and inference.

Combinatorial and algebraic perspectives on the marginal independence structure of Bayesian networks

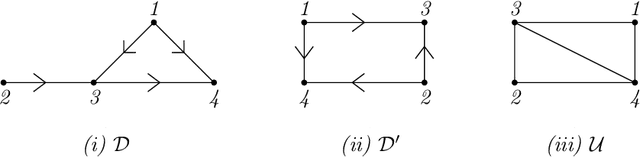
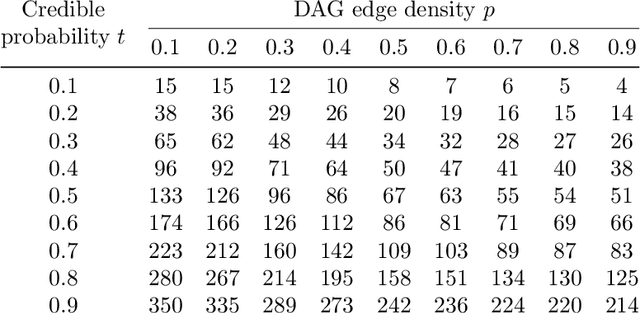
We consider the problem of estimating the marginal independence structure of a Bayesian network from observational data in the form of an undirected graph called the unconditional dependence graph. We show that unconditional dependence graphs correspond to the graphs having equal independence and intersection numbers. Using this observation, a Gr\"obner basis for a toric ideal associated to unconditional dependence graphs is given and then extended by additional binomial relations to connect the space of unconditional dependence graphs. An MCMC method, called GrUES (Gr\"obner-based Unconditional Equivalence Search), is implemented based on the resulting moves and applied to synthetic Gaussian data. GrUES recovers the true marginal independence structure via a BIC-optimal or MAP estimate at a higher rate than simple independence tests while also yielding an estimate of the posterior, for which the $20\%$ HPD credible sets include the true structure at a high rate for graphs with density at least $0.5$.

Causal Structure Learning with Greedy Unconditional Equivalence Search

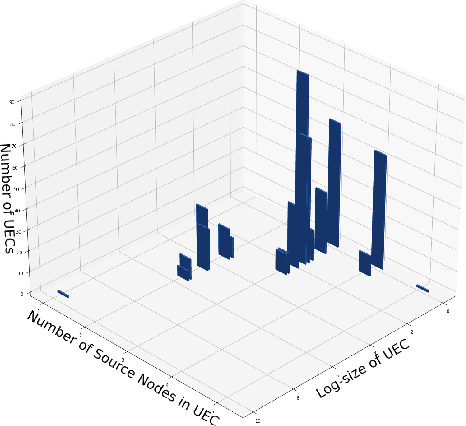
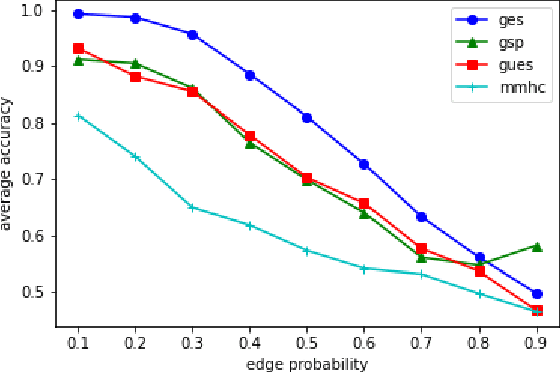
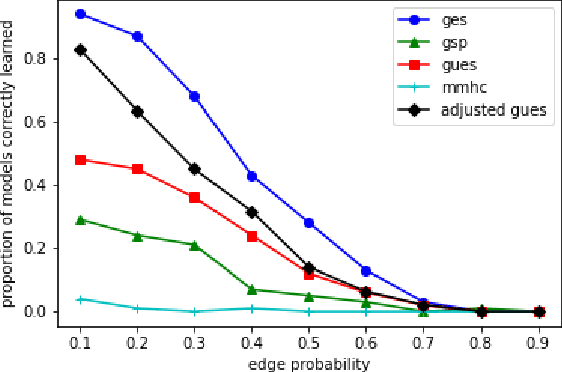
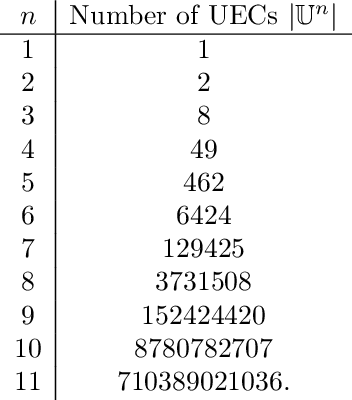
We consider the problem of characterizing directed acyclic graph (DAG) models up to unconditional equivalence, i.e., when two DAGs have the same set of unconditional d-separation statements. Each unconditional equivalence class (UEC) can be uniquely represented with an undirected graph whose clique structure encodes the members of the class. Via this structure, we provide a transformational characterization of unconditional equivalence. Combining these results, we introduce a hybrid algorithm for learning DAG models from observational data, called Greedy Unconditional Equivalence Search (GUES), which first estimates the UEC of the data using independence tests and then greedily searches the UEC for the optimal DAG. Applying GUES on synthetic data, we show that it achieves comparable accuracy to existing methods. However, in contrast to existing methods, since the average UEC is observed to contain few DAGs, the search space for GUES is drastically reduced.