Addressing pitfalls in implicit unobserved confounding synthesis using explicit block hierarchical ancestral sampling
Paper and Code
Mar 12, 2025
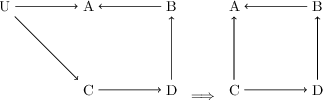
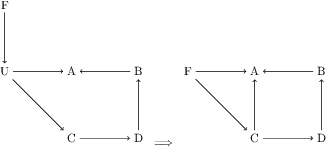
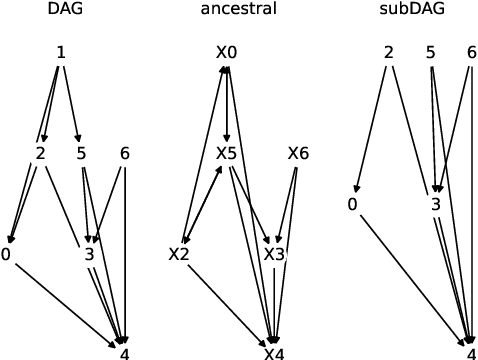
Unbiased data synthesis is crucial for evaluating causal discovery algorithms in the presence of unobserved confounding, given the scarcity of real-world datasets. A common approach, implicit parameterization, encodes unobserved confounding by modifying the off-diagonal entries of the idiosyncratic covariance matrix while preserving positive definiteness. Within this approach, state-of-the-art protocols have two distinct issues that hinder unbiased sampling from the complete space of causal models: first, the use of diagonally dominant constructions, which restrict the spectrum of partial correlation matrices; and second, the restriction of possible graphical structures when sampling bidirected edges, unnecessarily ruling out valid causal models. To address these limitations, we propose an improved explicit modeling approach for unobserved confounding, leveraging block-hierarchical ancestral generation of ground truth causal graphs. Algorithms for converting the ground truth DAG into ancestral graph is provided so that the output of causal discovery algorithms could be compared with. We prove that our approach fully covers the space of causal models, including those generated by the implicit parameterization, thus enabling more robust evaluation of methods for causal discovery and inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge