Sudoku Solver
Sudoku solver is a program that solves Sudoku puzzles by filling in the missing numbers based on the rules of the game.
Papers and Code
Can Continuous-Time Diffusion Models Generate and Solve Globally Constrained Discrete Problems? A Study on Sudoku
Jan 28, 2026Can standard continuous-time generative models represent distributions whose support is an extremely sparse, globally constrained discrete set? We study this question using completed Sudoku grids as a controlled testbed, treating them as a subset of a continuous relaxation space. We train flow-matching and score-based models along a Gaussian probability path and compare deterministic (ODE) sampling, stochastic (SDE) sampling, and DDPM-style discretizations derived from the same continuous-time training. Unconditionally, stochastic sampling substantially outperforms deterministic flows; score-based samplers are the most reliable among continuous-time methods, and DDPM-style ancestral sampling achieves the highest validity overall. We further show that the same models can be repurposed for guided generation: by repeatedly sampling completions under clamped clues and stopping when constraints are satisfied, the model acts as a probabilistic Sudoku solver. Although far less sample-efficient than classical solvers and discrete-geometry-aware diffusion methods, these experiments demonstrate that classic diffusion/flow formulations can assign non-zero probability mass to globally constrained combinatorial structures and can be used for constraint satisfaction via stochastic search.
Efficient Neuro-Symbolic Learning of Constraints and Objective
Aug 28, 2025In the ongoing quest for hybridizing discrete reasoning with neural nets, there is an increasing interest in neural architectures that can learn how to solve discrete reasoning or optimization problems from natural inputs, a task that Large Language Models seem to struggle with. Objectives: We introduce a differentiable neuro-symbolic architecture and a loss function dedicated to learning how to solve NP-hard reasoning problems. Methods: Our new probabilistic loss allows for learning both the constraints and the objective, thus delivering a complete model that can be scrutinized and completed with side constraints. By pushing the combinatorial solver out of the training loop, our architecture also offers scalable training while exact inference gives access to maximum accuracy. Results: We empirically show that it can efficiently learn how to solve NP-hard reasoning problems from natural inputs. On three variants of the Sudoku benchmark -- symbolic, visual, and many-solution --, our approach requires a fraction of training time of other hybrid methods. On a visual Min-Cut/Max-cut task, it optimizes the regret better than a Decision-Focused-Learning regret-dedicated loss. Finally, it efficiently learns the energy optimization formulation of the large real-world problem of designing proteins.
Sudoku-Bench: Evaluating creative reasoning with Sudoku variants
May 22, 2025



Existing reasoning benchmarks for large language models (LLMs) frequently fail to capture authentic creativity, often rewarding memorization of previously observed patterns. We address this shortcoming with Sudoku-Bench, a curated benchmark of challenging and unconventional Sudoku variants specifically selected to evaluate creative, multi-step logical reasoning. Sudoku variants form an unusually effective domain for reasoning research: each puzzle introduces unique or subtly interacting constraints, making memorization infeasible and requiring solvers to identify novel logical breakthroughs (``break-ins''). Despite their diversity, Sudoku variants maintain a common and compact structure, enabling clear and consistent evaluation. Sudoku-Bench includes a carefully chosen puzzle set, a standardized text-based puzzle representation, and flexible tools compatible with thousands of publicly available puzzles -- making it easy to extend into a general research environment. Baseline experiments show that state-of-the-art LLMs solve fewer than 15\% of puzzles unaided, highlighting significant opportunities to advance long-horizon, strategic reasoning capabilities.
Evaluating SAT and SMT Solvers on Large-Scale Sudoku Puzzles
Jan 15, 2025Modern SMT solvers have revolutionized the approach to constraint satisfaction problems by integrating advanced theory reasoning and encoding techniques. In this work, we evaluate the performance of modern SMT solvers in Z3, CVC5 and DPLL(T) against a standard SAT solver in DPLL. By benchmarking these solvers on novel, diverse 25x25 Sudoku puzzles of various difficulty levels created by our improved Sudoku generator, we examine the impact of advanced theory reasoning and encoding techniques. Our findings demonstrate that modern SMT solvers significantly outperform classical SAT solvers. This work highlights the evolution of logical solvers and exemplifies the utility of SMT solvers in addressing large-scale constraint satisfaction problems.
Causal Language Modeling Can Elicit Search and Reasoning Capabilities on Logic Puzzles
Sep 16, 2024



Causal language modeling using the Transformer architecture has yielded remarkable capabilities in Large Language Models (LLMs) over the last few years. However, the extent to which fundamental search and reasoning capabilities emerged within LLMs remains a topic of ongoing debate. In this work, we study if causal language modeling can learn a complex task such as solving Sudoku puzzles. To solve a Sudoku, the model is first required to search over all empty cells of the puzzle to decide on a cell to fill and then apply an appropriate strategy to fill the decided cell. Sometimes, the application of a strategy only results in thinning down the possible values in a cell rather than concluding the exact value of the cell. In such cases, multiple strategies are applied one after the other to fill a single cell. We observe that Transformer models trained on this synthetic task can indeed learn to solve Sudokus (our model solves $94.21\%$ of the puzzles fully correctly) when trained on a logical sequence of steps taken by a solver. We find that training Transformers with the logical sequence of steps is necessary and without such training, they fail to learn Sudoku. We also extend our analysis to Zebra puzzles (known as Einstein puzzles) and show that the model solves $92.04 \%$ of the puzzles fully correctly. In addition, we study the internal representations of the trained Transformer and find that through linear probing, we can decode information about the set of possible values in any given cell from them, pointing to the presence of a strong reasoning engine implicit in the Transformer weights.
Bridging Logic and Learning: A Neural-Symbolic Approach for Enhanced Reasoning in Neural Models
Dec 18, 2023Neural-symbolic learning, an intersection of neural networks and symbolic reasoning, aims to blend neural networks' learning capabilities with symbolic AI's interpretability and reasoning. This paper introduces an approach designed to improve the performance of neural models in learning reasoning tasks. It achieves this by integrating Answer Set Programming (ASP) solvers and domain-specific expertise, which is an approach that diverges from traditional complex neural-symbolic models. In this paper, a shallow artificial neural network (ANN) is specifically trained to solve Sudoku puzzles with minimal training data. The model has a unique loss function that integrates losses calculated using the ASP solver outputs, effectively enhancing its training efficiency. Most notably, the model shows a significant improvement in solving Sudoku puzzles using only 12 puzzles for training and testing without hyperparameter tuning. This advancement indicates that the model's enhanced reasoning capabilities have practical applications, extending well beyond Sudoku puzzles to potentially include a variety of other domains. The code can be found on GitHub: https://github.com/Fadi2200/ASPEN.
Neuro-Symbolic Sudoku Solver
Jul 02, 2023Deep Neural Networks have achieved great success in some of the complex tasks that humans can do with ease. These include image recognition/classification, natural language processing, game playing etc. However, modern Neural Networks fail or perform poorly when trained on tasks that can be solved easily using backtracking and traditional algorithms. Therefore, we use the architecture of the Neuro Logic Machine (NLM) and extend its functionality to solve a 9X9 game of Sudoku. To expand the application of NLMs, we generate a random grid of cells from a dataset of solved games and assign up to 10 new empty cells. The goal of the game is then to find a target value ranging from 1 to 9 and fill in the remaining empty cells while maintaining a valid configuration. In our study, we showcase an NLM which is capable of obtaining 100% accuracy for solving a Sudoku with empty cells ranging from 3 to 10. The purpose of this study is to demonstrate that NLMs can also be used for solving complex problems and games like Sudoku. We also analyze the behaviour of NLMs with a backtracking algorithm by comparing the convergence time using a graph plot on the same problem. With this study we show that Neural Logic Machines can be trained on the tasks that traditional Deep Learning architectures fail using Reinforcement Learning. We also aim to propose the importance of symbolic learning in explaining the systematicity in the hybrid model of NLMs.
Assessing SATNet's Ability to Solve the Symbol Grounding Problem
Dec 13, 2023SATNet is an award-winning MAXSAT solver that can be used to infer logical rules and integrated as a differentiable layer in a deep neural network. It had been shown to solve Sudoku puzzles visually from examples of puzzle digit images, and was heralded as an impressive achievement towards the longstanding AI goal of combining pattern recognition with logical reasoning. In this paper, we clarify SATNet's capabilities by showing that in the absence of intermediate labels that identify individual Sudoku digit images with their logical representations, SATNet completely fails at visual Sudoku (0% test accuracy). More generally, the failure can be pinpointed to its inability to learn to assign symbols to perceptual phenomena, also known as the symbol grounding problem, which has long been thought to be a prerequisite for intelligent agents to perform real-world logical reasoning. We propose an MNIST based test as an easy instance of the symbol grounding problem that can serve as a sanity check for differentiable symbolic solvers in general. Naive applications of SATNet on this test lead to performance worse than that of models without logical reasoning capabilities. We report on the causes of SATNet's failure and how to prevent them.
PuzzleBench: Can LLMs Solve Challenging First-Order Combinatorial Reasoning Problems?
Feb 04, 2024


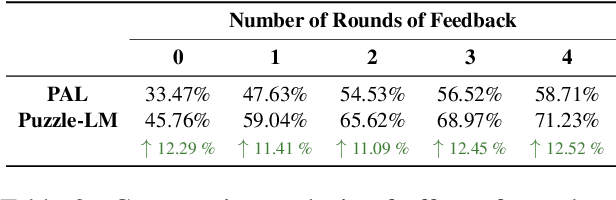
Recent works have explored the use of LLMs for reasoning tasks focussing on relatively simple problems, such as logical question answering. In our work, we wish to tackle more complicated problems, significantly expanding the capabilities of these models. Particularly, we explore whether LLMs can solve challenging first-order combinatorial reasoning problems, an example being the popular puzzle Sudoku. These problems have an underlying first-order structure described by a general description in natural language and can be instantiated to instances of varying sizes. Moreover these problems are computationally intensive requiring several reasoning steps to reach the solution. We present PuzzleBench a dataset of 31 such challenging puzzles. We observe that LLMs even when aided by symbolic solvers perform rather poorly on our benchmark. In response we propose a new approach, Puzzle-LM which combines LLMs with both symbolic solvers and program interpreters enabling them to reason about such challenging problems. We also show how feedback from smaller solved instances can help improve this reasoning ability.
Large Language Model Guided Tree-of-Thought
May 15, 2023In this paper, we introduce the Tree-of-Thought (ToT) framework, a novel approach aimed at improving the problem-solving capabilities of auto-regressive large language models (LLMs). The ToT technique is inspired by the human mind's approach for solving complex reasoning tasks through trial and error. In this process, the human mind explores the solution space through a tree-like thought process, allowing for backtracking when necessary. To implement ToT as a software system, we augment an LLM with additional modules including a prompter agent, a checker module, a memory module, and a ToT controller. In order to solve a given problem, these modules engage in a multi-round conversation with the LLM. The memory module records the conversation and state history of the problem solving process, which allows the system to backtrack to the previous steps of the thought-process and explore other directions from there. To verify the effectiveness of the proposed technique, we implemented a ToT-based solver for the Sudoku Puzzle. Experimental results show that the ToT framework can significantly increase the success rate of Sudoku puzzle solving. Our implementation of the ToT-based Sudoku solver is available on GitHub: \url{https://github.com/jieyilong/tree-of-thought-puzzle-solver}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge