A Solver-Free Framework for Scalable Learning in Neural ILP Architectures
Paper and Code
Oct 17, 2022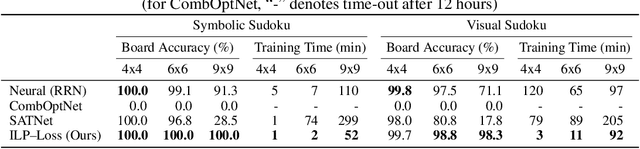
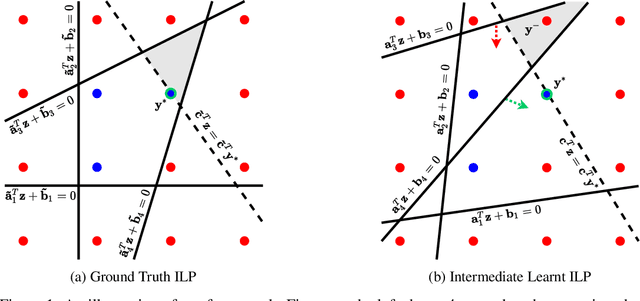
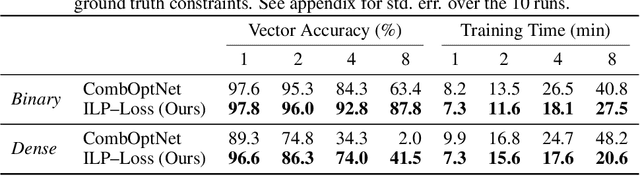

There is a recent focus on designing architectures that have an Integer Linear Programming (ILP) layer within a neural model (referred to as Neural ILP in this paper). Neural ILP architectures are suitable for pure reasoning tasks that require data-driven constraint learning or for tasks requiring both perception (neural) and reasoning (ILP). A recent SOTA approach for end-to-end training of Neural ILP explicitly defines gradients through the ILP black box (Paulus et al. 2021) - this trains extremely slowly, owing to a call to the underlying ILP solver for every training data point in a minibatch. In response, we present an alternative training strategy that is solver-free, i.e., does not call the ILP solver at all at training time. Neural ILP has a set of trainable hyperplanes (for cost and constraints in ILP), together representing a polyhedron. Our key idea is that the training loss should impose that the final polyhedron separates the positives (all constraints satisfied) from the negatives (at least one violated constraint or a suboptimal cost value), via a soft-margin formulation. While positive example(s) are provided as part of the training data, we devise novel techniques for generating negative samples. Our solution is flexible enough to handle equality as well as inequality constraints. Experiments on several problems, both perceptual as well as symbolic, which require learning the constraints of an ILP, show that our approach has superior performance and scales much better compared to purely neural baselines and other state-of-the-art models that require solver-based training. In particular, we are able to obtain excellent performance in 9 x 9 symbolic and visual sudoku, to which the other Neural ILP solver is not able to scale.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge