ReLU neural network approximation to piecewise constant functions

This paper studies the approximation property of ReLU neural networks (NNs) to piecewise constant functions with unknown interfaces in bounded regions in $\mathbb{R}^d$. Under the assumption that the discontinuity interface $\Gamma$ may be approximated by a connected series of hyperplanes with a prescribed accuracy $\varepsilon >0$, we show that a three-layer ReLU NN is sufficient to accurately approximate any piecewise constant function and establish its error bound. Moreover, if the discontinuity interface is convex, an analytical formula of the ReLU NN approximation with exact weights and biases is provided.

Dynamic PDB: A New Dataset and a SE(3) Model Extension by Integrating Dynamic Behaviors and Physical Properties in Protein Structures

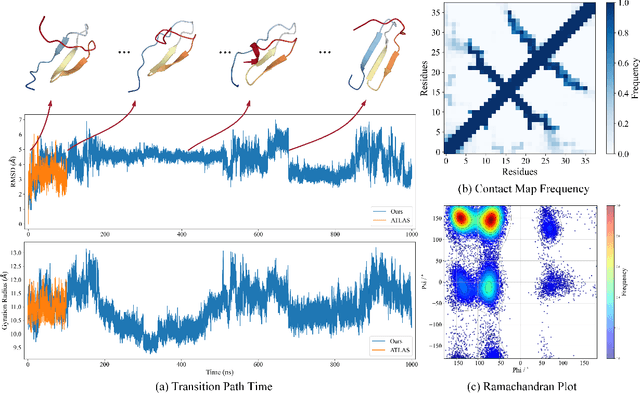
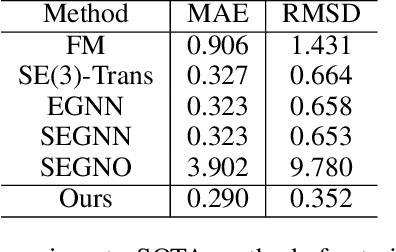
Despite significant progress in static protein structure collection and prediction, the dynamic behavior of proteins, one of their most vital characteristics, has been largely overlooked in prior research. This oversight can be attributed to the limited availability, diversity, and heterogeneity of dynamic protein datasets. To address this gap, we propose to enhance existing prestigious static 3D protein structural databases, such as the Protein Data Bank (PDB), by integrating dynamic data and additional physical properties. Specifically, we introduce a large-scale dataset, Dynamic PDB, encompassing approximately 12.6K proteins, each subjected to all-atom molecular dynamics (MD) simulations lasting 1 microsecond to capture conformational changes. Furthermore, we provide a comprehensive suite of physical properties, including atomic velocities and forces, potential and kinetic energies of proteins, and the temperature of the simulation environment, recorded at 1 picosecond intervals throughout the simulations. For benchmarking purposes, we evaluate state-of-the-art methods on the proposed dataset for the task of trajectory prediction. To demonstrate the value of integrating richer physical properties in the study of protein dynamics and related model design, we base our approach on the SE(3) diffusion model and incorporate these physical properties into the trajectory prediction process. Preliminary results indicate that this straightforward extension of the SE(3) model yields improved accuracy, as measured by MAE and RMSD, when the proposed physical properties are taken into consideration.

Fast Iterative Solver For Neural Network Method: II. 1D Diffusion-Reaction Problems And Data Fitting

This paper expands the damped block Newton (dBN) method introduced recently in [4] for 1D diffusion-reaction equations and least-squares data fitting problems. To determine the linear parameters (the weights and bias of the output layer) of the neural network (NN), the dBN method requires solving systems of linear equations involving the mass matrix. While the mass matrix for local hat basis functions is tri-diagonal and well-conditioned, the mass matrix for NNs is dense and ill-conditioned. For example, the condition number of the NN mass matrix for quasi-uniform meshes is at least ${\cal O}(n^4)$. We present a factorization of the mass matrix that enables solving the systems of linear equations in ${\cal O}(n)$ operations. To determine the non-linear parameters (the weights and bias of the hidden layer), one step of a damped Newton method is employed at each iteration. A Gauss-Newton method is used in place of Newton for the instances in which the Hessian matrices are singular. This modified dBN is referred to as dBGN. For both methods, the computational cost per iteration is ${\cal O}(n)$. Numerical results demonstrate the ability dBN and dBGN to efficiently achieve accurate results and outperform BFGS for select examples.

Weak Generative Sampler to Efficiently Sample Invariant Distribution of Stochastic Differential Equation

Sampling invariant distributions from an Ito diffusion process presents a significant challenge in stochastic simulation. Traditional numerical solvers for stochastic differential equations require both a fine step size and a lengthy simulation period, resulting in both biased and correlated samples. Current deep learning-based method solves the stationary Fokker--Planck equation to determine the invariant probability density function in form of deep neural networks, but they generally do not directly address the problem of sampling from the computed density function. In this work, we introduce a framework that employs a weak generative sampler (WGS) to directly generate independent and identically distributed (iid) samples induced by a transformation map derived from the stationary Fokker--Planck equation. Our proposed loss function is based on the weak form of the Fokker--Planck equation, integrating normalizing flows to characterize the invariant distribution and facilitate sample generation from the base distribution. Our randomized test function circumvents the need for mini-max optimization in the traditional weak formulation. Distinct from conventional generative models, our method neither necessitates the computationally intensive calculation of the Jacobian determinant nor the invertibility of the transformation map. A crucial component of our framework is the adaptively chosen family of test functions in the form of Gaussian kernel functions with centres selected from the generated data samples. Experimental results on several benchmark examples demonstrate the effectiveness of our method, which offers both low computational costs and excellent capability in exploring multiple metastable states.

A Structure-Guided Gauss-Newton Method for Shallow ReLU Neural Network

In this paper, we propose a structure-guided Gauss-Newton (SgGN) method for solving least squares problems using a shallow ReLU neural network. The method effectively takes advantage of both the least squares structure and the neural network structure of the objective function. By categorizing the weights and biases of the hidden and output layers of the network as nonlinear and linear parameters, respectively, the method iterates back and forth between the nonlinear and linear parameters. The nonlinear parameters are updated by a damped Gauss-Newton method and the linear ones are updated by a linear solver. Moreover, at the Gauss-Newton step, a special form of the Gauss-Newton matrix is derived for the shallow ReLU neural network and is used for efficient iterations. It is shown that the corresponding mass and Gauss-Newton matrices in the respective linear and nonlinear steps are symmetric and positive definite under reasonable assumptions. Thus, the SgGN method naturally produces an effective search direction without the need of additional techniques like shifting in the Levenberg-Marquardt method to achieve invertibility of the Gauss-Newton matrix. The convergence and accuracy of the method are demonstrated numerically for several challenging function approximation problems, especially those with discontinuities or sharp transition layers that pose significant challenges for commonly used training algorithms in machine learning.

Qubit-Wise Architecture Search Method for Variational Quantum Circuits

Considering the noise level limit, one crucial aspect for quantum machine learning is to design a high-performing variational quantum circuit architecture with small number of quantum gates. As the classical neural architecture search (NAS), quantum architecture search methods (QAS) employ methods like reinforcement learning, evolutionary algorithms and supernet optimiza-tion to improve the search efficiency. In this paper, we propose a novel qubit-wise architec-ture search (QWAS) method, which progres-sively search one-qubit configuration per stage, and combine with Monte Carlo Tree Search al-gorithm to find good quantum architectures by partitioning the search space into several good and bad subregions. The numerical experimental results indicate that our proposed method can balance the exploration and exploitation of cir-cuit performance and size in some real-world tasks, such as MNIST, Fashion and MOSI. As far as we know, QWAS achieves the state-of-art re-sults of all tasks in the terms of accuracy and circuit size.

Residual-Quantile Adjustment for Adaptive Training of Physics-informed Neural Network

Adaptive training methods for physical-informed neural network (PINN) require dedicated constructions of the distribution of weights assigned at each training sample. To efficiently seek such an optimal weight distribution is not a simple task and most existing methods choose the adaptive weights based on approximating the full distribution or the maximum of residuals. In this paper, we show that the bottleneck in the adaptive choice of samples for training efficiency is the behavior of the tail distribution of the numerical residual. Thus, we propose the Residual-Quantile Adjustment (RQA) method for a better weight choice for each training sample. After initially setting the weights proportional to the $p$-th power of the residual, our RQA method reassign all weights above $q$-quantile ($90\%$ for example) to the median value, so that the weight follows a quantile-adjusted distribution derived from the residuals. With the iterative reweighting technique, RQA is also very easy to implement. Experiment results show that the proposed method can outperform several adaptive methods on various partial differential equation (PDE) problems.

Learn Quasi-stationary Distributions of Finite State Markov Chain

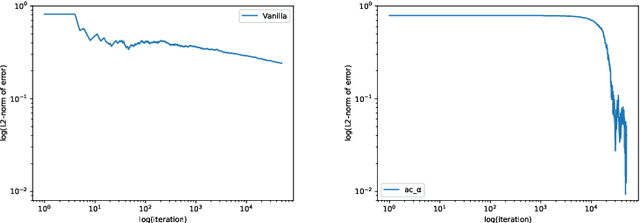
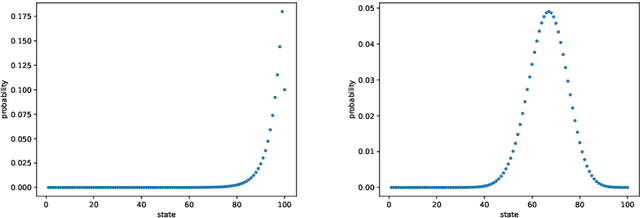
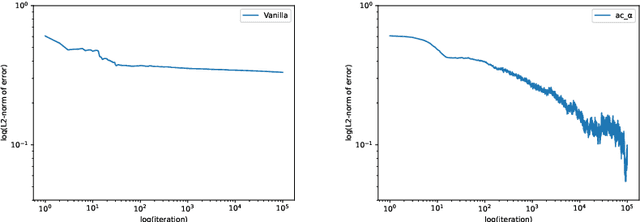
We propose a reinforcement learning (RL) approach to compute the expression of quasi-stationary distribution. Based on the fixed-point formulation of quasi-stationary distribution, we minimize the KL-divergence of two Markovian path distributions induced by the candidate distribution and the true target distribution. To solve this challenging minimization problem by gradient descent, we apply the reinforcement learning technique by introducing the corresponding reward and value functions. We derive the corresponding policy gradient theorem and design an actor-critic algorithm to learn the optimal solution and value function. The numerical examples of finite state Markov chain are tested to demonstrate the new methods

Finite Volume Least-Squares Neural Network (FV-LSNN) Method for Scalar Nonlinear Hyperbolic Conservation Laws

In [4], we introduced the least-squares ReLU neural network (LSNN) method for solving the linear advection-reaction problem with discontinuous solution and showed that the number of degrees of freedom for the LSNN method is significantly less than that of traditional mesh-based methods. The LSNN method is a discretization of an equivalent least-squares (LS) formulation in the class of neural network functions with the ReLU activation function; and evaluation of the LS functional is done by using numerical integration and proper numerical differentiation. By developing a novel finite volume approximation (FVA) to the divergence operator, this paper studies the LSNN method for scalar nonlinear hyperbolic conservation laws. The FVA introduced in this paper is tailored to the LSNN method and is more accurate than traditional, well-studied FV schemes used in mesh-based numerical methods. Numerical results of some benchmark test problems with both convex and non-convex fluxes show that the finite volume LSNN (FV-LSNN) method is capable of computing the physical solution for problems with rarefaction waves and capturing the shock of the underlying problem automatically through the free hyper-planes of the ReLU neural network. Moreover, the method does not exhibit the common Gibbs phenomena along the discontinuous interface.

Self-adaptive deep neural network: Numerical approximation to functions and PDEs

Designing an optimal deep neural network for a given task is important and challenging in many machine learning applications. To address this issue, we introduce a self-adaptive algorithm: the adaptive network enhancement (ANE) method, written as loops of the form train, estimate and enhance. Starting with a small two-layer neural network (NN), the step train is to solve the optimization problem at the current NN; the step estimate is to compute a posteriori estimator/indicators using the solution at the current NN; the step enhance is to add new neurons to the current NN. Novel network enhancement strategies based on the computed estimator/indicators are developed in this paper to determine how many new neurons and when a new layer should be added to the current NN. The ANE method provides a natural process for obtaining a good initialization in training the current NN; in addition, we introduce an advanced procedure on how to initialize newly added neurons for a better approximation. We demonstrate that the ANE method can automatically design a nearly minimal NN for learning functions exhibiting sharp transitional layers as well as discontinuous solutions of hyperbolic partial differential equations.