Finite Volume Least-Squares Neural Network (FV-LSNN) Method for Scalar Nonlinear Hyperbolic Conservation Laws

In [4], we introduced the least-squares ReLU neural network (LSNN) method for solving the linear advection-reaction problem with discontinuous solution and showed that the number of degrees of freedom for the LSNN method is significantly less than that of traditional mesh-based methods. The LSNN method is a discretization of an equivalent least-squares (LS) formulation in the class of neural network functions with the ReLU activation function; and evaluation of the LS functional is done by using numerical integration and proper numerical differentiation. By developing a novel finite volume approximation (FVA) to the divergence operator, this paper studies the LSNN method for scalar nonlinear hyperbolic conservation laws. The FVA introduced in this paper is tailored to the LSNN method and is more accurate than traditional, well-studied FV schemes used in mesh-based numerical methods. Numerical results of some benchmark test problems with both convex and non-convex fluxes show that the finite volume LSNN (FV-LSNN) method is capable of computing the physical solution for problems with rarefaction waves and capturing the shock of the underlying problem automatically through the free hyper-planes of the ReLU neural network. Moreover, the method does not exhibit the common Gibbs phenomena along the discontinuous interface.

Self-adaptive deep neural network: Numerical approximation to functions and PDEs

Designing an optimal deep neural network for a given task is important and challenging in many machine learning applications. To address this issue, we introduce a self-adaptive algorithm: the adaptive network enhancement (ANE) method, written as loops of the form train, estimate and enhance. Starting with a small two-layer neural network (NN), the step train is to solve the optimization problem at the current NN; the step estimate is to compute a posteriori estimator/indicators using the solution at the current NN; the step enhance is to add new neurons to the current NN. Novel network enhancement strategies based on the computed estimator/indicators are developed in this paper to determine how many new neurons and when a new layer should be added to the current NN. The ANE method provides a natural process for obtaining a good initialization in training the current NN; in addition, we introduce an advanced procedure on how to initialize newly added neurons for a better approximation. We demonstrate that the ANE method can automatically design a nearly minimal NN for learning functions exhibiting sharp transitional layers as well as discontinuous solutions of hyperbolic partial differential equations.

Least-Squares ReLU Neural Network Method For Linear Advection-Reaction Equation

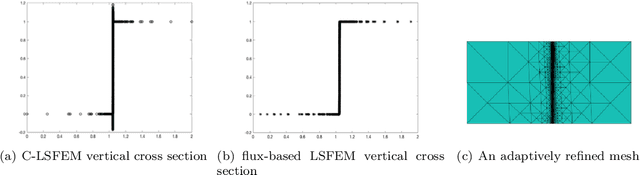
This paper studies least-squares ReLU neural network method for solving the linear advection-reaction problem with discontinuous solution. The method is a discretization of an equivalent least-squares formulation in the set of neural network functions with the ReLU activation function. The method is capable of approximating the discontinuous interface of the underlying problem automatically through the free hyper-planes of the ReLU neural network and, hence, outperforms mesh-based numerical methods in terms of the number of degrees of freedom. Numerical results of some benchmark test problems show that the method can not only approximate the solution with the least number of parameters, but also avoid the common Gibbs phenomena along the discontinuous interface. Moreover, a three-layer ReLU neural network is necessary and sufficient in order to well approximate a discontinuous solution with an interface in $\mathbb{R}^2$ that is not a straight line.

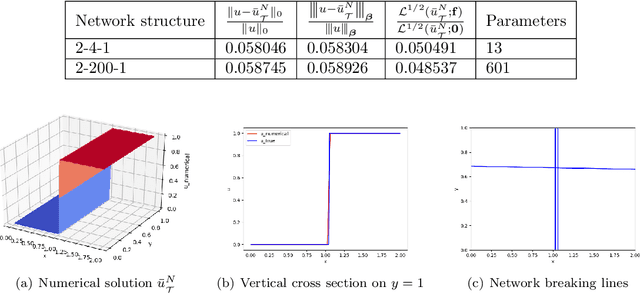
Least-Squares ReLU Neural Network Method For Scalar Nonlinear Hyperbolic Conservation Law

We introduced the least-squares ReLU neural network (LSNN) method for solving the linear advection-reaction problem with discontinuous solution and showed that the method outperforms mesh-based numerical methods in terms of the number of degrees of freedom. This paper studies the LSNN method for scalar nonlinear hyperbolic conservation law. The method is a discretization of an equivalent least-squares (LS) formulation in the set of neural network functions with the ReLU activation function. Evaluation of the LS functional is done by using numerical integration and conservative finite volume scheme. Numerical results of some test problems show that the method is capable of approximating the discontinuous interface of the underlying problem automatically through the free breaking lines of the ReLU neural network. Moreover, the method does not exhibit the common Gibbs phenomena along the discontinuous interface.

Deep least-squares methods: an unsupervised learning-based numerical method for solving elliptic PDEs

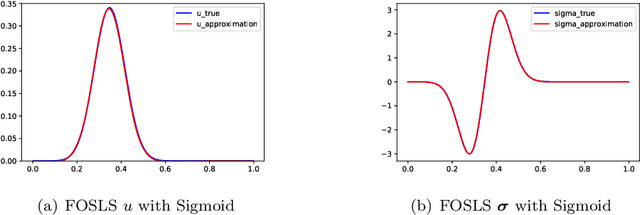
This paper studies an unsupervised deep learning-based numerical approach for solving partial differential equations (PDEs). The approach makes use of the deep neural network to approximate solutions of PDEs through the compositional construction and employs least-squares functionals as loss functions to determine parameters of the deep neural network. There are various least-squares functionals for a partial differential equation. This paper focuses on the so-called first-order system least-squares (FOSLS) functional studied in [3], which is based on a first-order system of scalar second-order elliptic PDEs. Numerical results for second-order elliptic PDEs in one dimension are presented.