Learn Quasi-stationary Distributions of Finite State Markov Chain

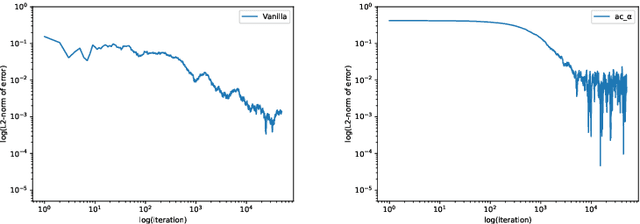
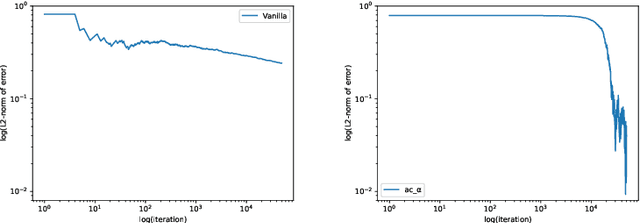
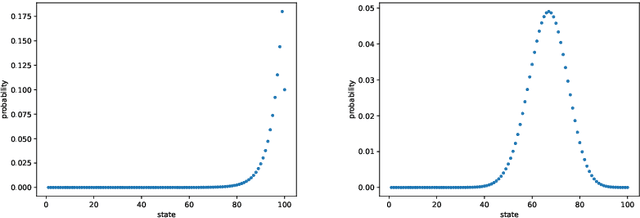
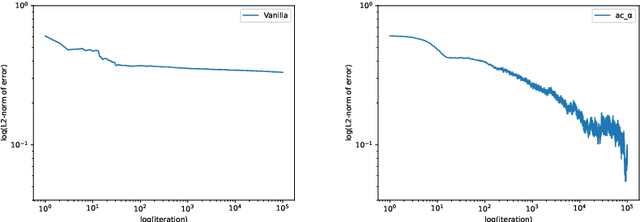
We propose a reinforcement learning (RL) approach to compute the expression of quasi-stationary distribution. Based on the fixed-point formulation of quasi-stationary distribution, we minimize the KL-divergence of two Markovian path distributions induced by the candidate distribution and the true target distribution. To solve this challenging minimization problem by gradient descent, we apply the reinforcement learning technique by introducing the corresponding reward and value functions. We derive the corresponding policy gradient theorem and design an actor-critic algorithm to learn the optimal solution and value function. The numerical examples of finite state Markov chain are tested to demonstrate the new methods