Fast Iterative Solver For Neural Network Method: II. 1D Diffusion-Reaction Problems And Data Fitting
Paper and Code
Jul 01, 2024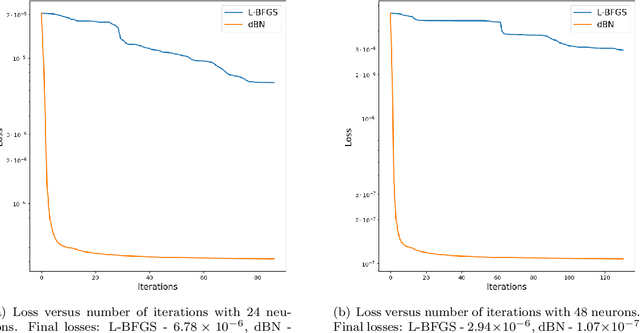
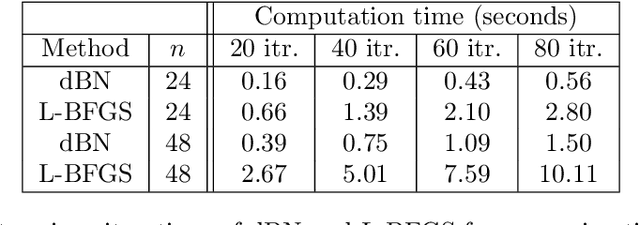
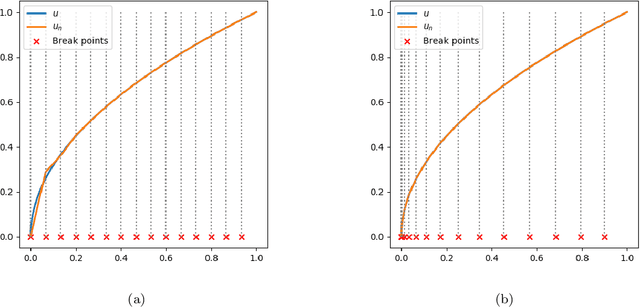
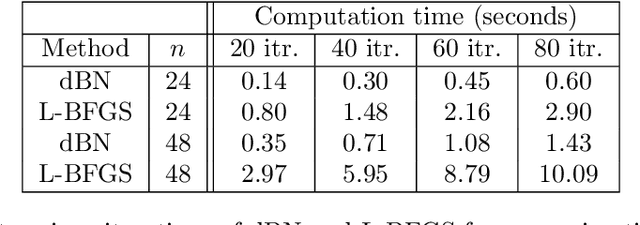
This paper expands the damped block Newton (dBN) method introduced recently in [4] for 1D diffusion-reaction equations and least-squares data fitting problems. To determine the linear parameters (the weights and bias of the output layer) of the neural network (NN), the dBN method requires solving systems of linear equations involving the mass matrix. While the mass matrix for local hat basis functions is tri-diagonal and well-conditioned, the mass matrix for NNs is dense and ill-conditioned. For example, the condition number of the NN mass matrix for quasi-uniform meshes is at least ${\cal O}(n^4)$. We present a factorization of the mass matrix that enables solving the systems of linear equations in ${\cal O}(n)$ operations. To determine the non-linear parameters (the weights and bias of the hidden layer), one step of a damped Newton method is employed at each iteration. A Gauss-Newton method is used in place of Newton for the instances in which the Hessian matrices are singular. This modified dBN is referred to as dBGN. For both methods, the computational cost per iteration is ${\cal O}(n)$. Numerical results demonstrate the ability dBN and dBGN to efficiently achieve accurate results and outperform BFGS for select examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge