Bidirectional Linear Recurrent Models for Sequence-Level Multisource Fusion

Sequence modeling is a critical yet challenging task with wide-ranging applications, especially in time series forecasting for domains like weather prediction, temperature monitoring, and energy load forecasting. Transformers, with their attention mechanism, have emerged as state-of-the-art due to their efficient parallel training, but they suffer from quadratic time complexity, limiting their scalability for long sequences. In contrast, recurrent neural networks (RNNs) offer linear time complexity, spurring renewed interest in linear RNNs for more computationally efficient sequence modeling. In this work, we introduce BLUR (Bidirectional Linear Unit for Recurrent network), which uses forward and backward linear recurrent units (LRUs) to capture both past and future dependencies with high computational efficiency. BLUR maintains the linear time complexity of traditional RNNs, while enabling fast parallel training through LRUs. Furthermore, it offers provably stable training and strong approximation capabilities, making it highly effective for modeling long-term dependencies. Extensive experiments on sequential image and time series datasets reveal that BLUR not only surpasses transformers and traditional RNNs in accuracy but also significantly reduces computational costs, making it particularly suitable for real-world forecasting tasks. Our code is available here.

FUSE: First-Order and Second-Order Unified SynthEsis in Stochastic Optimization

Stochastic optimization methods have actively been playing a critical role in modern machine learning algorithms to deliver decent performance. While numerous works have proposed and developed diverse approaches, first-order and second-order methods are in entirely different situations. The former is significantly pivotal and dominating in emerging deep learning but only leads convergence to a stationary point. However, second-order methods are less popular due to their computational intensity in large-dimensional problems. This paper presents a novel method that leverages both the first-order and second-order methods in a unified algorithmic framework, termed FUSE, from which a practical version (PV) is derived accordingly. FUSE-PV stands as a simple yet efficient optimization method involving a switch-over between first and second orders. Additionally, we develop different criteria that determine when to switch. FUSE-PV has provably shown a smaller computational complexity than SGD and Adam. To validate our proposed scheme, we present an ablation study on several simple test functions and show a comparison with baselines for benchmark datasets.

Enhancing PPO with Trajectory-Aware Hybrid Policies

Proximal policy optimization (PPO) is one of the most popular state-of-the-art on-policy algorithms that has become a standard baseline in modern reinforcement learning with applications in numerous fields. Though it delivers stable performance with theoretical policy improvement guarantees, high variance, and high sample complexity still remain critical challenges in on-policy algorithms. To alleviate these issues, we propose Hybrid-Policy Proximal Policy Optimization (HP3O), which utilizes a trajectory replay buffer to make efficient use of trajectories generated by recent policies. Particularly, the buffer applies the "first in, first out" (FIFO) strategy so as to keep only the recent trajectories to attenuate the data distribution drift. A batch consisting of the trajectory with the best return and other randomly sampled ones from the buffer is used for updating the policy networks. The strategy helps the agent to improve its capability on top of the most recent best performance and in turn reduce variance empirically. We theoretically construct the policy improvement guarantees for the proposed algorithm. HP3O is validated and compared against several baseline algorithms using multiple continuous control environments. Our code is available here.

RLS3: RL-Based Synthetic Sample Selection to Enhance Spatial Reasoning in Vision-Language Models for Indoor Autonomous Perception

Vision-language model (VLM) fine-tuning for application-specific visual grounding based on natural language instructions has become one of the most popular approaches for learning-enabled autonomous systems. However, such fine-tuning relies heavily on high-quality datasets to achieve successful performance in various downstream tasks. Additionally, VLMs often encounter limitations due to insufficient and imbalanced fine-tuning data. To address these issues, we propose a new generalizable framework to improve VLM fine-tuning by integrating it with a reinforcement learning (RL) agent. Our method utilizes the RL agent to manipulate objects within an indoor setting to create synthetic data for fine-tuning to address certain vulnerabilities of the VLM. Specifically, we use the performance of the VLM to provide feedback to the RL agent to generate informative data that efficiently fine-tune the VLM over the targeted task (e.g. spatial reasoning). The key contribution of this work is developing a framework where the RL agent serves as an informative data sampling tool and assists the VLM in order to enhance performance and address task-specific vulnerabilities. By targeting the data sampling process to address the weaknesses of the VLM, we can effectively train a more context-aware model. In addition, generating synthetic data allows us to have precise control over each scene and generate granular ground truth captions. Our results show that the proposed data generation approach improves the spatial reasoning performance of VLMs, which demonstrates the benefits of using RL-guided data generation in vision-language tasks.

STITCH: Surface reconstrucTion using Implicit neural representations with Topology Constraints and persistent Homology

We present STITCH, a novel approach for neural implicit surface reconstruction of a sparse and irregularly spaced point cloud while enforcing topological constraints (such as having a single connected component). We develop a new differentiable framework based on persistent homology to formulate topological loss terms that enforce the prior of a single 2-manifold object. Our method demonstrates excellent performance in preserving the topology of complex 3D geometries, evident through both visual and empirical comparisons. We supplement this with a theoretical analysis, and provably show that optimizing the loss with stochastic (sub)gradient descent leads to convergence and enables reconstructing shapes with a single connected component. Our approach showcases the integration of differentiable topological data analysis tools for implicit surface reconstruction.

FAWAC: Feasibility Informed Advantage Weighted Regression for Persistent Safety in Offline Reinforcement Learning

Safe offline reinforcement learning aims to learn policies that maximize cumulative rewards while adhering to safety constraints, using only offline data for training. A key challenge is balancing safety and performance, particularly when the policy encounters out-of-distribution (OOD) states and actions, which can lead to safety violations or overly conservative behavior during deployment. To address these challenges, we introduce Feasibility Informed Advantage Weighted Actor-Critic (FAWAC), a method that prioritizes persistent safety in constrained Markov decision processes (CMDPs). FAWAC formulates policy optimization with feasibility conditions derived specifically for offline datasets, enabling safe policy updates in non-parametric policy space, followed by projection into parametric space for constrained actor training. By incorporating a cost-advantage term into Advantage Weighted Regression (AWR), FAWAC ensures that the safety constraints are respected while maximizing performance. Additionally, we propose a strategy to address a more challenging class of problems that involves tempting datasets where trajectories are predominantly high-rewarded but unsafe. Empirical evaluations on standard benchmarks demonstrate that FAWAC achieves strong results, effectively balancing safety and performance in learning policies from the static datasets.

Latent Safety-Constrained Policy Approach for Safe Offline Reinforcement Learning

In safe offline reinforcement learning (RL), the objective is to develop a policy that maximizes cumulative rewards while strictly adhering to safety constraints, utilizing only offline data. Traditional methods often face difficulties in balancing these constraints, leading to either diminished performance or increased safety risks. We address these issues with a novel approach that begins by learning a conservatively safe policy through the use of Conditional Variational Autoencoders, which model the latent safety constraints. Subsequently, we frame this as a Constrained Reward-Return Maximization problem, wherein the policy aims to optimize rewards while complying with the inferred latent safety constraints. This is achieved by training an encoder with a reward-Advantage Weighted Regression objective within the latent constraint space. Our methodology is supported by theoretical analysis, including bounds on policy performance and sample complexity. Extensive empirical evaluation on benchmark datasets, including challenging autonomous driving scenarios, demonstrates that our approach not only maintains safety compliance but also excels in cumulative reward optimization, surpassing existing methods. Additional visualizations provide further insights into the effectiveness and underlying mechanisms of our approach.

DIMAT: Decentralized Iterative Merging-And-Training for Deep Learning Models

Recent advances in decentralized deep learning algorithms have demonstrated cutting-edge performance on various tasks with large pre-trained models. However, a pivotal prerequisite for achieving this level of competitiveness is the significant communication and computation overheads when updating these models, which prohibits the applications of them to real-world scenarios. To address this issue, drawing inspiration from advanced model merging techniques without requiring additional training, we introduce the Decentralized Iterative Merging-And-Training (DIMAT) paradigm--a novel decentralized deep learning framework. Within DIMAT, each agent is trained on their local data and periodically merged with their neighboring agents using advanced model merging techniques like activation matching until convergence is achieved. DIMAT provably converges with the best available rate for nonconvex functions with various first-order methods, while yielding tighter error bounds compared to the popular existing approaches. We conduct a comprehensive empirical analysis to validate DIMAT's superiority over baselines across diverse computer vision tasks sourced from multiple datasets. Empirical results validate our theoretical claims by showing that DIMAT attains faster and higher initial gain in accuracy with independent and identically distributed (IID) and non-IID data, incurring lower communication overhead. This DIMAT paradigm presents a new opportunity for the future decentralized learning, enhancing its adaptability to real-world with sparse and light-weight communication and computation.

Neural PDE Solvers for Irregular Domains

Neural network-based approaches for solving partial differential equations (PDEs) have recently received special attention. However, the large majority of neural PDE solvers only apply to rectilinear domains, and do not systematically address the imposition of Dirichlet/Neumann boundary conditions over irregular domain boundaries. In this paper, we present a framework to neurally solve partial differential equations over domains with irregularly shaped (non-rectilinear) geometric boundaries. Our network takes in the shape of the domain as an input (represented using an unstructured point cloud, or any other parametric representation such as Non-Uniform Rational B-Splines) and is able to generalize to novel (unseen) irregular domains; the key technical ingredient to realizing this model is a novel approach for identifying the interior and exterior of the computational grid in a differentiable manner. We also perform a careful error analysis which reveals theoretical insights into several sources of error incurred in the model-building process. Finally, we showcase a wide variety of applications, along with favorable comparisons with ground truth solutions.

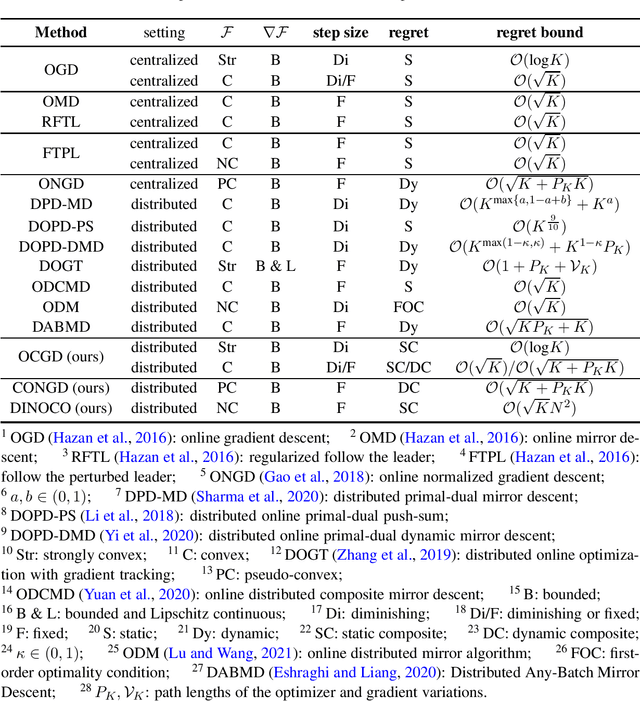
Distributed Online Non-convex Optimization with Composite Regret

Regret has been widely adopted as the metric of choice for evaluating the performance of online optimization algorithms for distributed, multi-agent systems. However, data/model variations associated with agents can significantly impact decisions and requires consensus among agents. Moreover, most existing works have focused on developing approaches for (either strongly or non-strongly) convex losses, and very few results have been obtained regarding regret bounds in distributed online optimization for general non-convex losses. To address these two issues, we propose a novel composite regret with a new network regret-based metric to evaluate distributed online optimization algorithms. We concretely define static and dynamic forms of the composite regret. By leveraging the dynamic form of our composite regret, we develop a consensus-based online normalized gradient (CONGD) approach for pseudo-convex losses, and it provably shows a sublinear behavior relating to a regularity term for the path variation of the optimizer. For general non-convex losses, we first shed light on the regret for the setting of distributed online non-convex learning based on recent advances such that no deterministic algorithm can achieve the sublinear regret. We then develop the distributed online non-convex optimization with composite regret (DINOCO) without access to the gradients, depending on an offline optimization oracle. DINOCO is shown to achieve sublinear regret; to our knowledge, this is the first regret bound for general distributed online non-convex learning.