Geometry Matters: Benchmarking Scientific ML Approaches for Flow Prediction around Complex Geometries

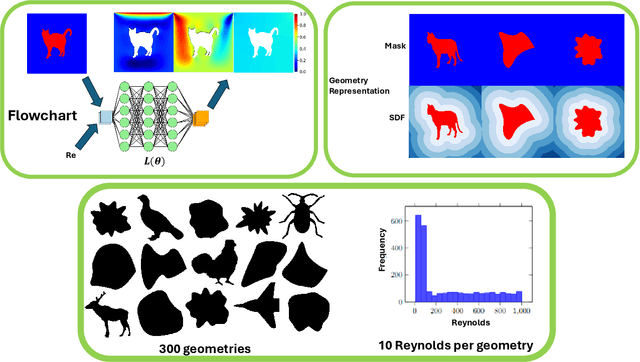
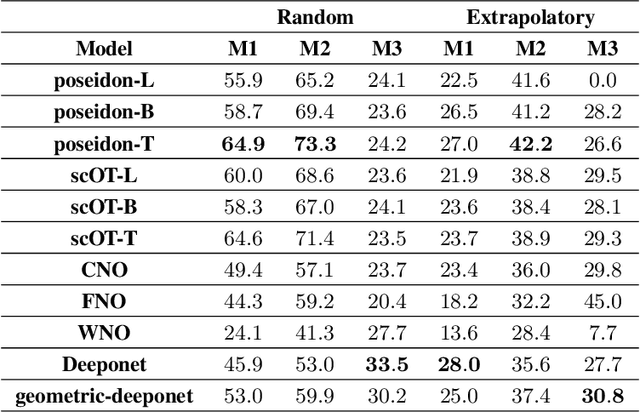
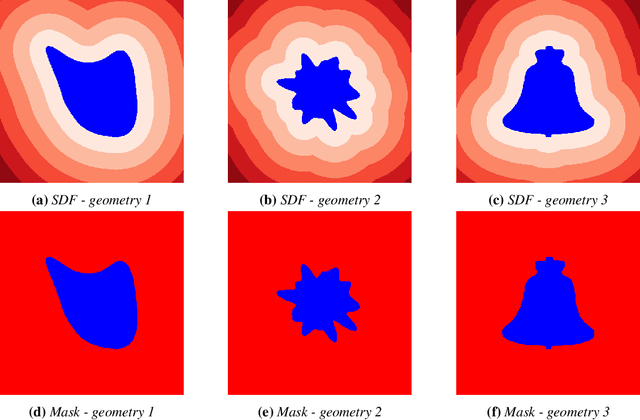
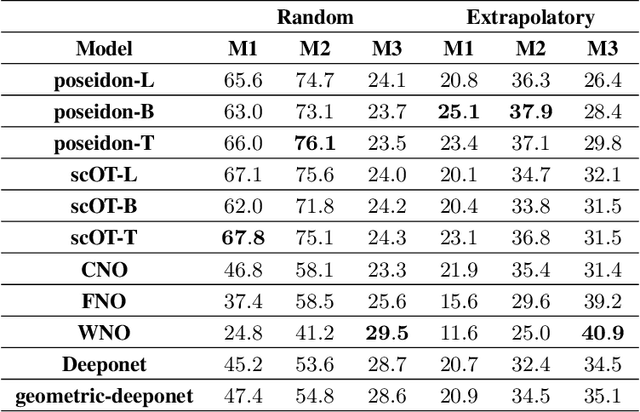
Rapid yet accurate simulations of fluid dynamics around complex geometries is critical in a variety of engineering and scientific applications, including aerodynamics and biomedical flows. However, while scientific machine learning (SciML) has shown promise, most studies are constrained to simple geometries, leaving complex, real-world scenarios underexplored. This study addresses this gap by benchmarking diverse SciML models, including neural operators and vision transformer-based foundation models, for fluid flow prediction over intricate geometries. Using a high-fidelity dataset of steady-state flows across various geometries, we evaluate the impact of geometric representations -- Signed Distance Fields (SDF) and binary masks -- on model accuracy, scalability, and generalization. Central to this effort is the introduction of a novel, unified scoring framework that integrates metrics for global accuracy, boundary layer fidelity, and physical consistency to enable a robust, comparative evaluation of model performance. Our findings demonstrate that foundation models significantly outperform neural operators, particularly in data-limited scenarios, and that SDF representations yield superior results with sufficient training data. Despite these advancements, all models struggle with out-of-distribution generalization, highlighting a critical challenge for future SciML applications. By advancing both evaluation methodologies and modeling capabilities, this work paves the way for robust and scalable ML solutions for fluid dynamics across complex geometries.

STITCH: Surface reconstrucTion using Implicit neural representations with Topology Constraints and persistent Homology

We present STITCH, a novel approach for neural implicit surface reconstruction of a sparse and irregularly spaced point cloud while enforcing topological constraints (such as having a single connected component). We develop a new differentiable framework based on persistent homology to formulate topological loss terms that enforce the prior of a single 2-manifold object. Our method demonstrates excellent performance in preserving the topology of complex 3D geometries, evident through both visual and empirical comparisons. We supplement this with a theoretical analysis, and provably show that optimizing the loss with stochastic (sub)gradient descent leads to convergence and enables reconstructing shapes with a single connected component. Our approach showcases the integration of differentiable topological data analysis tools for implicit surface reconstruction.

3D Reconstruction of Protein Structures from Multi-view AFM Images using Neural Radiance Fields (NeRFs)

Recent advancements in deep learning for predicting 3D protein structures have shown promise, particularly when leveraging inputs like protein sequences and Cryo-Electron microscopy (Cryo-EM) images. However, these techniques often fall short when predicting the structures of protein complexes (PCs), which involve multiple proteins. In our study, we investigate using atomic force microscopy (AFM) combined with deep learning to predict the 3D structures of PCs. AFM generates height maps that depict the PCs in various random orientations, providing a rich information for training a neural network to predict the 3D structures. We then employ the pre-trained UpFusion model (which utilizes a conditional diffusion model for synthesizing novel views) to train an instance-specific NeRF model for 3D reconstruction. The performance of UpFusion is evaluated through zero-shot predictions of 3D protein structures using AFM images. The challenge, however, lies in the time-intensive and impractical nature of collecting actual AFM images. To address this, we use a virtual AFM imaging process that transforms a `PDB' protein file into multi-view 2D virtual AFM images via volume rendering techniques. We extensively validate the UpFusion architecture using both virtual and actual multi-view AFM images. Our results include a comparison of structures predicted with varying numbers of views and different sets of views. This novel approach holds significant potential for enhancing the accuracy of protein complex structure predictions with further fine-tuning of the UpFusion network.

Latent Diffusion Models for Structural Component Design

Recent advances in generative modeling, namely Diffusion models, have revolutionized generative modeling, enabling high-quality image generation tailored to user needs. This paper proposes a framework for the generative design of structural components. Specifically, we employ a Latent Diffusion model to generate potential designs of a component that can satisfy a set of problem-specific loading conditions. One of the distinct advantages our approach offers over other generative approaches, such as generative adversarial networks (GANs), is that it permits the editing of existing designs. We train our model using a dataset of geometries obtained from structural topology optimization utilizing the SIMP algorithm. Consequently, our framework generates inherently near-optimal designs. Our work presents quantitative results that support the structural performance of the generated designs and the variability in potential candidate designs. Furthermore, we provide evidence of the scalability of our framework by operating over voxel domains with resolutions varying from $32^3$ to $128^3$. Our framework can be used as a starting point for generating novel near-optimal designs similar to topology-optimized designs.

Neural PDE Solvers for Irregular Domains

Neural network-based approaches for solving partial differential equations (PDEs) have recently received special attention. However, the large majority of neural PDE solvers only apply to rectilinear domains, and do not systematically address the imposition of Dirichlet/Neumann boundary conditions over irregular domain boundaries. In this paper, we present a framework to neurally solve partial differential equations over domains with irregularly shaped (non-rectilinear) geometric boundaries. Our network takes in the shape of the domain as an input (represented using an unstructured point cloud, or any other parametric representation such as Non-Uniform Rational B-Splines) and is able to generalize to novel (unseen) irregular domains; the key technical ingredient to realizing this model is a novel approach for identifying the interior and exterior of the computational grid in a differentiable manner. We also perform a careful error analysis which reveals theoretical insights into several sources of error incurred in the model-building process. Finally, we showcase a wide variety of applications, along with favorable comparisons with ground truth solutions.

Cross-Gradient Aggregation for Decentralized Learning from Non-IID data

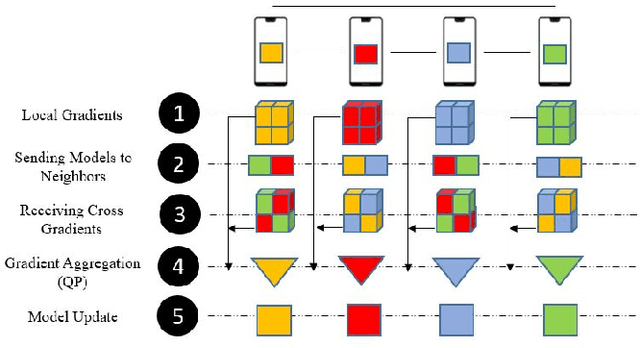
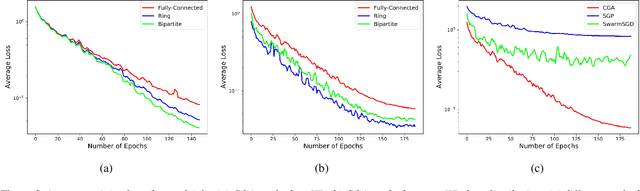
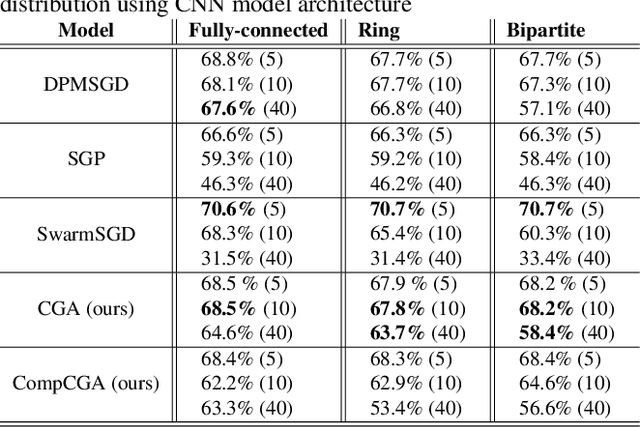
Decentralized learning enables a group of collaborative agents to learn models using a distributed dataset without the need for a central parameter server. Recently, decentralized learning algorithms have demonstrated state-of-the-art results on benchmark data sets, comparable with centralized algorithms. However, the key assumption to achieve competitive performance is that the data is independently and identically distributed (IID) among the agents which, in real-life applications, is often not applicable. Inspired by ideas from continual learning, we propose Cross-Gradient Aggregation (CGA), a novel decentralized learning algorithm where (i) each agent aggregates cross-gradient information, i.e., derivatives of its model with respect to its neighbors' datasets, and (ii) updates its model using a projected gradient based on quadratic programming (QP). We theoretically analyze the convergence characteristics of CGA and demonstrate its efficiency on non-IID data distributions sampled from the MNIST and CIFAR-10 datasets. Our empirical comparisons show superior learning performance of CGA over existing state-of-the-art decentralized learning algorithms, as well as maintaining the improved performance under information compression to reduce peer-to-peer communication overhead.

Physics-consistent deep learning for structural topology optimization

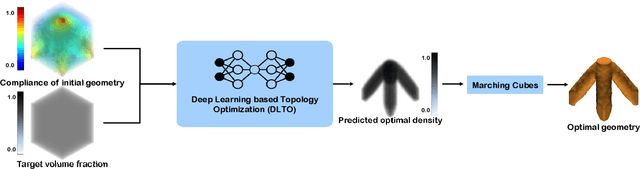
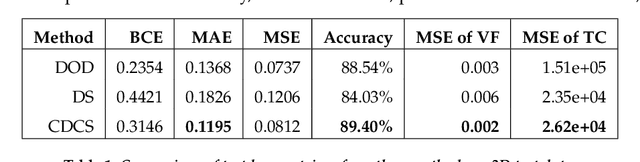
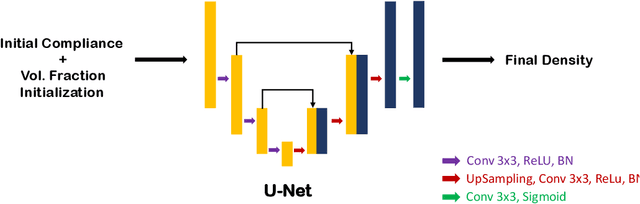
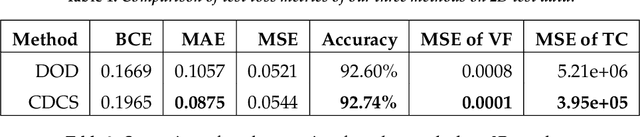
Topology optimization has emerged as a popular approach to refine a component's design and increasing its performance. However, current state-of-the-art topology optimization frameworks are compute-intensive, mainly due to multiple finite element analysis iterations required to evaluate the component's performance during the optimization process. Recently, machine learning-based topology optimization methods have been explored by researchers to alleviate this issue. However, previous approaches have mainly been demonstrated on simple two-dimensional applications with low-resolution geometry. Further, current approaches are based on a single machine learning model for end-to-end prediction, which requires a large dataset for training. These challenges make it non-trivial to extend the current approaches to higher resolutions. In this paper, we explore a deep learning-based framework for performing topology optimization for three-dimensional geometries with a reasonably fine (high) resolution. We are able to achieve this by training multiple networks, each trying to learn a different aspect of the overall topology optimization methodology. We demonstrate the application of our framework on both 2D and 3D geometries. The results show that our approach predicts the final optimized design better than current ML-based topology optimization methods.