Who Gets the Reward, Who Gets the Blame? Evaluation-Aligned Training Signals for Multi-LLM Agents

Large Language Models (LLMs) in multi-agent systems (MAS) have shown promise for complex tasks, yet current training methods lack principled ways to connect system-level evaluation with agent-level and message-level learning. We propose a theoretical framework that unifies cooperative game-theoretic attribution with process reward modeling to transform system evaluation into agent credit and then into response-level signals. Unlike prior approaches that rely only on attribution (e.g., Shapley) or step-level labels (e.g., PRM), our method produces local, signed, and credit-conserving signals. In success cases, Shapley-based credit assignment fairly allocates outcomes across agents and is refined into per-message rewards that promote cooperation while discouraging redundancy or sabotage. In failure cases, first-error localization yields repair-aware preferences that penalize harmful steps while rewarding corrective attempts. The resulting signals are bounded, cooperative, and directly compatible with reinforcement-based or preference-based post-training, providing a unified and auditable pathway from global evaluation to local supervision in LLM multi-agent training. Our contribution is conceptual: we present a theoretical foundation and training signals, leaving empirical validation for future work.

Arboretum: A Large Multimodal Dataset Enabling AI for Biodiversity

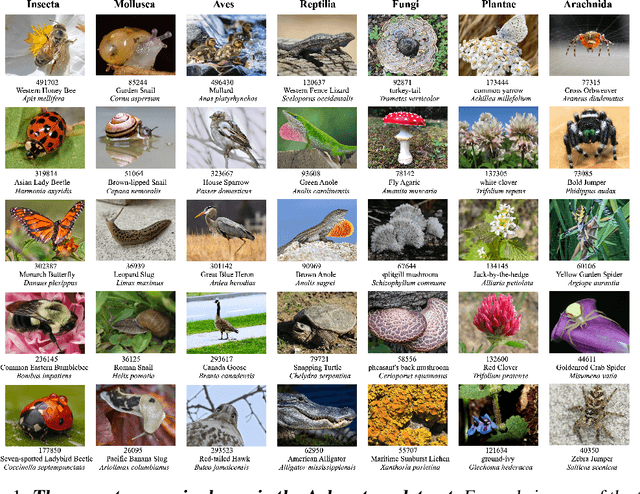
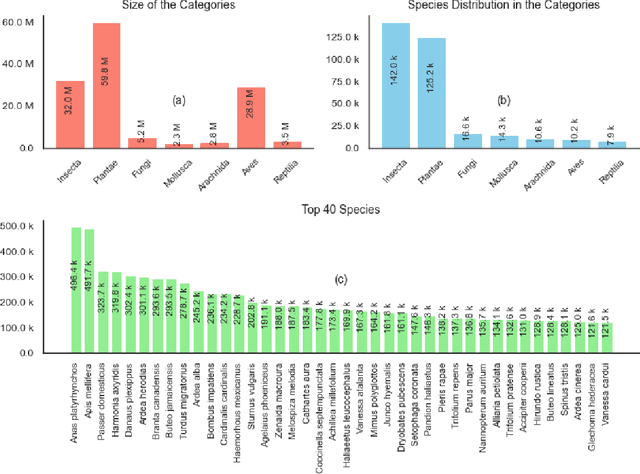
We introduce Arboretum, the largest publicly accessible dataset designed to advance AI for biodiversity applications. This dataset, curated from the iNaturalist community science platform and vetted by domain experts to ensure accuracy, includes 134.6 million images, surpassing existing datasets in scale by an order of magnitude. The dataset encompasses image-language paired data for a diverse set of species from birds (Aves), spiders/ticks/mites (Arachnida), insects (Insecta), plants (Plantae), fungus/mushrooms (Fungi), snails (Mollusca), and snakes/lizards (Reptilia), making it a valuable resource for multimodal vision-language AI models for biodiversity assessment and agriculture research. Each image is annotated with scientific names, taxonomic details, and common names, enhancing the robustness of AI model training. We showcase the value of Arboretum by releasing a suite of CLIP models trained using a subset of 40 million captioned images. We introduce several new benchmarks for rigorous assessment, report accuracy for zero-shot learning, and evaluations across life stages, rare species, confounding species, and various levels of the taxonomic hierarchy. We anticipate that Arboretum will spur the development of AI models that can enable a variety of digital tools ranging from pest control strategies, crop monitoring, and worldwide biodiversity assessment and environmental conservation. These advancements are critical for ensuring food security, preserving ecosystems, and mitigating the impacts of climate change. Arboretum is publicly available, easily accessible, and ready for immediate use. Please see the \href{https://baskargroup.github.io/Arboretum/}{project website} for links to our data, models, and code.

Neural PDE Solvers for Irregular Domains

Neural network-based approaches for solving partial differential equations (PDEs) have recently received special attention. However, the large majority of neural PDE solvers only apply to rectilinear domains, and do not systematically address the imposition of Dirichlet/Neumann boundary conditions over irregular domain boundaries. In this paper, we present a framework to neurally solve partial differential equations over domains with irregularly shaped (non-rectilinear) geometric boundaries. Our network takes in the shape of the domain as an input (represented using an unstructured point cloud, or any other parametric representation such as Non-Uniform Rational B-Splines) and is able to generalize to novel (unseen) irregular domains; the key technical ingredient to realizing this model is a novel approach for identifying the interior and exterior of the computational grid in a differentiable manner. We also perform a careful error analysis which reveals theoretical insights into several sources of error incurred in the model-building process. Finally, we showcase a wide variety of applications, along with favorable comparisons with ground truth solutions.