3D Neural Operator-Based Flow Surrogates around 3D geometries: Signed Distance Functions and Derivative Constraints

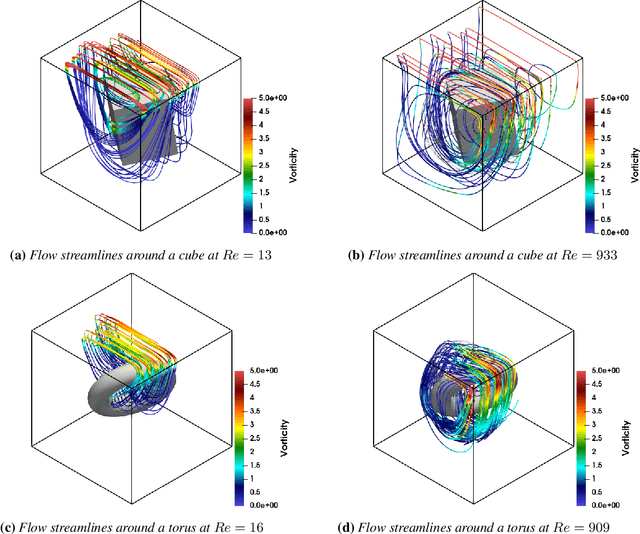
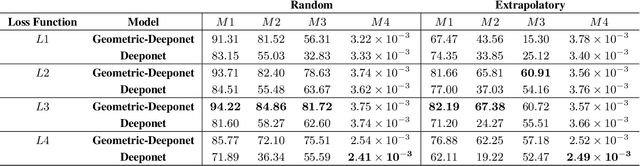
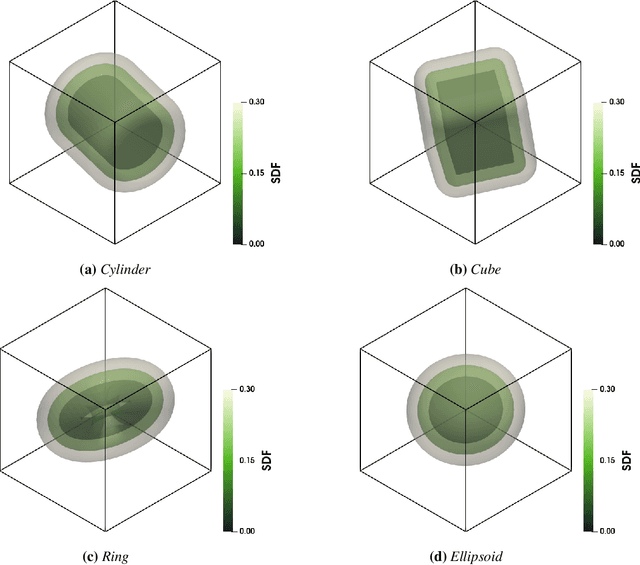
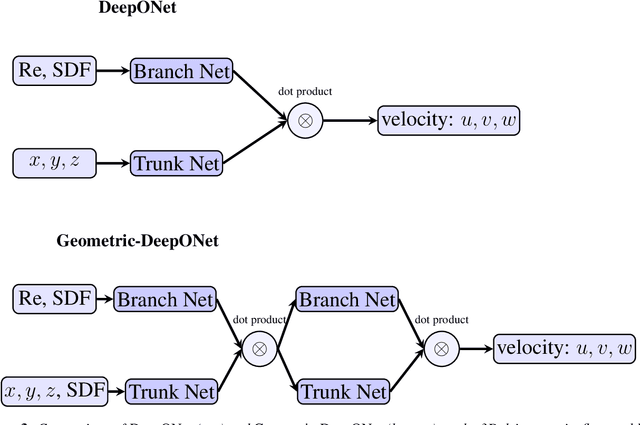
Accurate modeling of fluid dynamics around complex geometries is critical for applications such as aerodynamic optimization and biomedical device design. While advancements in numerical methods and high-performance computing have improved simulation capabilities, the computational cost of high-fidelity 3D flow simulations remains a significant challenge. Scientific machine learning (SciML) offers an efficient alternative, enabling rapid and reliable flow predictions. In this study, we evaluate Deep Operator Networks (DeepONet) and Geometric-DeepONet, a variant that incorporates geometry information via signed distance functions (SDFs), on steady-state 3D flow over complex objects. Our dataset consists of 1,000 high-fidelity simulations spanning Reynolds numbers from 10 to 1,000, enabling comprehensive training and evaluation across a range of flow regimes. To assess model generalization, we test our models on a random and extrapolatory train-test splitting. Additionally, we explore a derivative-informed training strategy that augments standard loss functions with velocity gradient penalties and incompressibility constraints, improving physics consistency in 3D flow prediction. Our results show that Geometric-DeepONet improves boundary-layer accuracy by up to 32% compared to standard DeepONet. Moreover, incorporating derivative constraints enhances gradient accuracy by 25% in interpolation tasks and up to 45% in extrapolatory test scenarios, suggesting significant improvement in generalization capabilities to unseen 3D Reynolds numbers.

Geometry Matters: Benchmarking Scientific ML Approaches for Flow Prediction around Complex Geometries

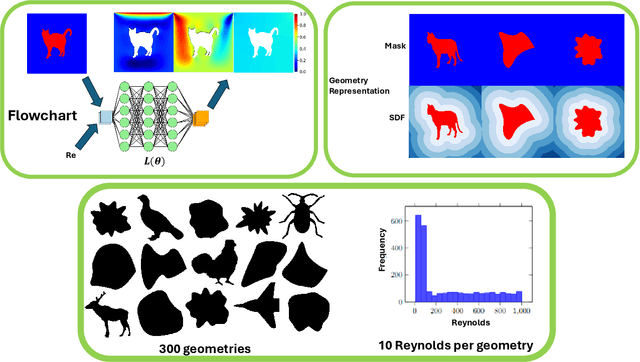
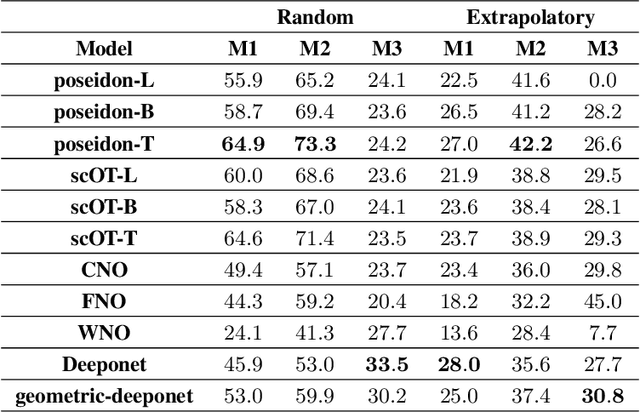
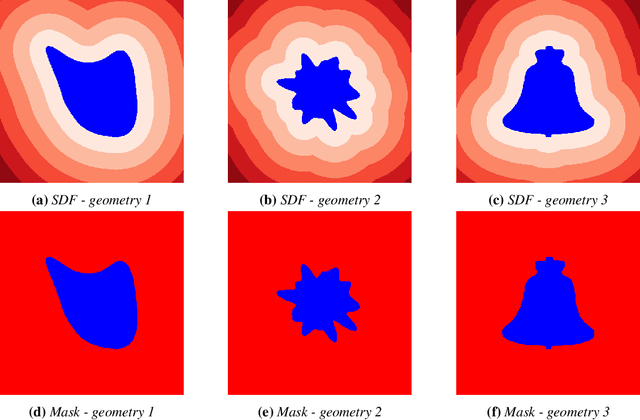
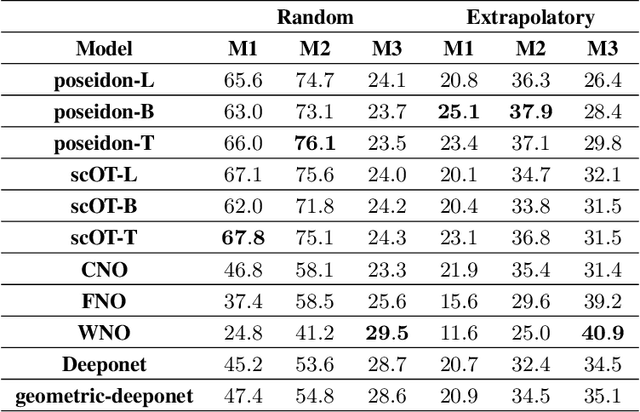
Rapid yet accurate simulations of fluid dynamics around complex geometries is critical in a variety of engineering and scientific applications, including aerodynamics and biomedical flows. However, while scientific machine learning (SciML) has shown promise, most studies are constrained to simple geometries, leaving complex, real-world scenarios underexplored. This study addresses this gap by benchmarking diverse SciML models, including neural operators and vision transformer-based foundation models, for fluid flow prediction over intricate geometries. Using a high-fidelity dataset of steady-state flows across various geometries, we evaluate the impact of geometric representations -- Signed Distance Fields (SDF) and binary masks -- on model accuracy, scalability, and generalization. Central to this effort is the introduction of a novel, unified scoring framework that integrates metrics for global accuracy, boundary layer fidelity, and physical consistency to enable a robust, comparative evaluation of model performance. Our findings demonstrate that foundation models significantly outperform neural operators, particularly in data-limited scenarios, and that SDF representations yield superior results with sufficient training data. Despite these advancements, all models struggle with out-of-distribution generalization, highlighting a critical challenge for future SciML applications. By advancing both evaluation methodologies and modeling capabilities, this work paves the way for robust and scalable ML solutions for fluid dynamics across complex geometries.

FlowBench: A Large Scale Benchmark for Flow Simulation over Complex Geometries

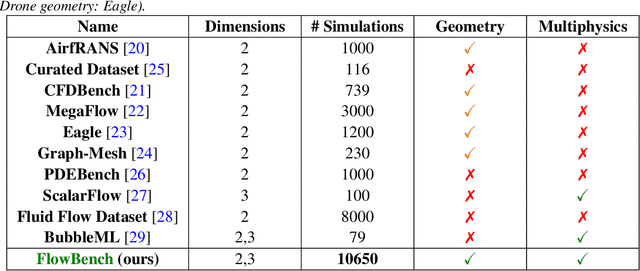
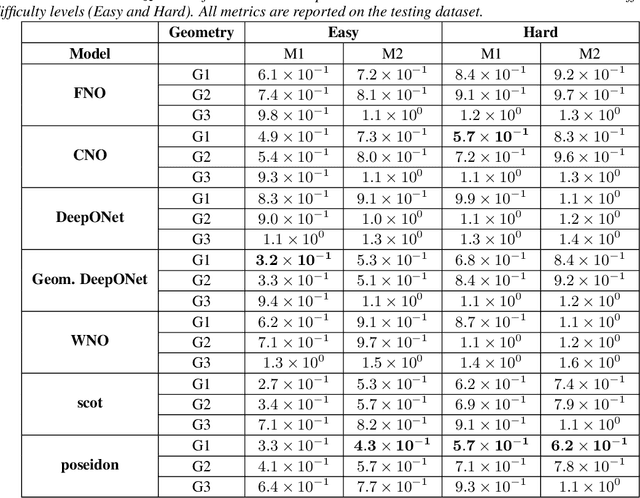
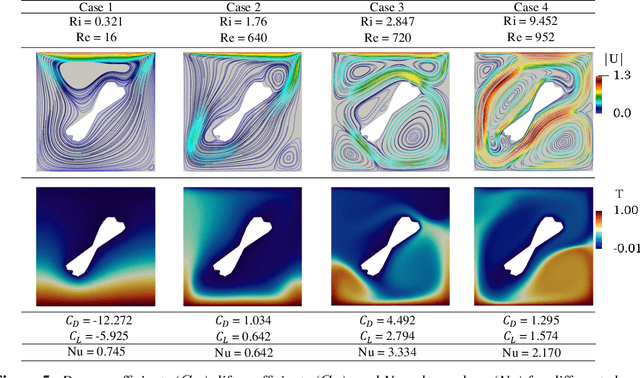
Simulating fluid flow around arbitrary shapes is key to solving various engineering problems. However, simulating flow physics across complex geometries remains numerically challenging and computationally resource-intensive, particularly when using conventional PDE solvers. Machine learning methods offer attractive opportunities to create fast and adaptable PDE solvers. However, benchmark datasets to measure the performance of such methods are scarce, especially for flow physics across complex geometries. We introduce FlowBench, a dataset for neural simulators with over 10K samples, which is currently larger than any publicly available flow physics dataset. FlowBench contains flow simulation data across complex geometries (\textit{parametric vs. non-parametric}), spanning a range of flow conditions (\textit{Reynolds number and Grashoff number}), capturing a diverse array of flow phenomena (\textit{steady vs. transient; forced vs. free convection}), and for both 2D and 3D. FlowBench contains over 10K data samples, with each sample the outcome of a fully resolved, direct numerical simulation using a well-validated simulator framework designed for modeling transport phenomena in complex geometries. For each sample, we include velocity, pressure, and temperature field data at 3 different resolutions and several summary statistics features of engineering relevance (such as coefficients of lift and drag, and Nusselt numbers). %Additionally, we include masks and signed distance fields for each shape. We envision that FlowBench will enable evaluating the interplay between complex geometry, coupled flow phenomena, and data sufficiency on the performance of current, and future, neural PDE solvers. We enumerate several evaluation metrics to help rank order the performance of neural PDE solvers. We benchmark the performance of several baseline methods including FNO, CNO, WNO, and DeepONet.