Distributed Online Non-convex Optimization with Composite Regret
Paper and Code
Sep 21, 2022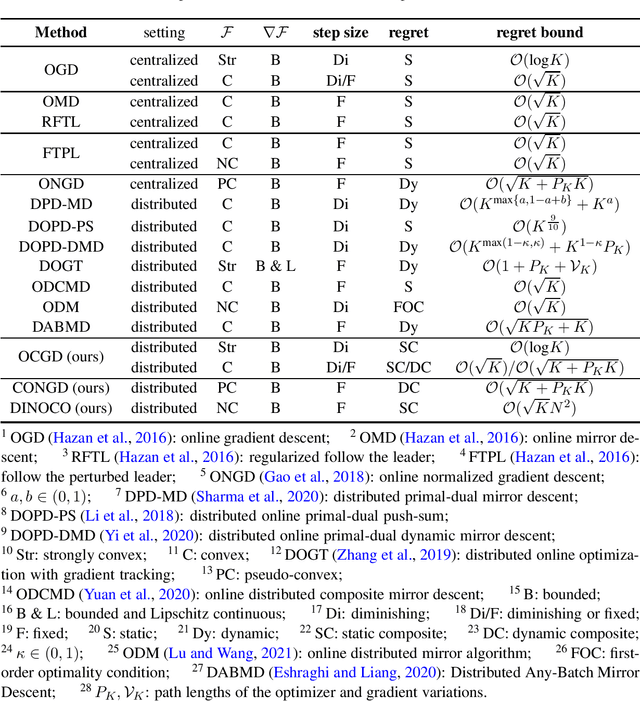
Regret has been widely adopted as the metric of choice for evaluating the performance of online optimization algorithms for distributed, multi-agent systems. However, data/model variations associated with agents can significantly impact decisions and requires consensus among agents. Moreover, most existing works have focused on developing approaches for (either strongly or non-strongly) convex losses, and very few results have been obtained regarding regret bounds in distributed online optimization for general non-convex losses. To address these two issues, we propose a novel composite regret with a new network regret-based metric to evaluate distributed online optimization algorithms. We concretely define static and dynamic forms of the composite regret. By leveraging the dynamic form of our composite regret, we develop a consensus-based online normalized gradient (CONGD) approach for pseudo-convex losses, and it provably shows a sublinear behavior relating to a regularity term for the path variation of the optimizer. For general non-convex losses, we first shed light on the regret for the setting of distributed online non-convex learning based on recent advances such that no deterministic algorithm can achieve the sublinear regret. We then develop the distributed online non-convex optimization with composite regret (DINOCO) without access to the gradients, depending on an offline optimization oracle. DINOCO is shown to achieve sublinear regret; to our knowledge, this is the first regret bound for general distributed online non-convex learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge