SWE-Factory: Your Automated Factory for Issue Resolution Training Data and Evaluation Benchmarks

Constructing large-scale datasets for the GitHub issue resolution task is crucial for both training and evaluating the software engineering capabilities of Large Language Models (LLMs). However, the traditional process for creating such benchmarks is notoriously challenging and labor-intensive, particularly in the stages of setting up evaluation environments, grading test outcomes, and validating task instances. In this paper, we propose SWE-Factory, an automated pipeline designed to address these challenges. To tackle these issues, our pipeline integrates three core automated components. First, we introduce SWE-Builder, a multi-agent system that automates evaluation environment construction, which employs four specialized agents that work in a collaborative, iterative loop and leverages an environment memory pool to enhance efficiency. Second, we introduce a standardized, exit-code-based grading method that eliminates the need for manually writing custom parsers. Finally, we automate the fail2pass validation process using these reliable exit code signals. Experiments on 671 issues across four programming languages show that our pipeline can effectively construct valid task instances; for example, with GPT-4.1-mini, our SWE-Builder constructs 269 valid instances at $0.045 per instance, while with Gemini-2.5-flash, it achieves comparable performance at the lowest cost of $0.024 per instance. We also demonstrate that our exit-code-based grading achieves 100% accuracy compared to manual inspection, and our automated fail2pass validation reaches a precision of 0.92 and a recall of 1.00. We hope our automated pipeline will accelerate the collection of large-scale, high-quality GitHub issue resolution datasets for both training and evaluation. Our code and datasets are released at https://github.com/DeepSoftwareAnalytics/swe-factory.

MoQAE: Mixed-Precision Quantization for Long-Context LLM Inference via Mixture of Quantization-Aware Experts

One of the primary challenges in optimizing large language models (LLMs) for long-context inference lies in the high memory consumption of the Key-Value (KV) cache. Existing approaches, such as quantization, have demonstrated promising results in reducing memory usage. However, current quantization methods cannot take both effectiveness and efficiency into account. In this paper, we propose MoQAE, a novel mixed-precision quantization method via mixture of quantization-aware experts. First, we view different quantization bit-width configurations as experts and use the traditional mixture of experts (MoE) method to select the optimal configuration. To avoid the inefficiency caused by inputting tokens one by one into the router in the traditional MoE method, we input the tokens into the router chunk by chunk. Second, we design a lightweight router-only fine-tuning process to train MoQAE with a comprehensive loss to learn the trade-off between model accuracy and memory usage. Finally, we introduce a routing freezing (RF) and a routing sharing (RS) mechanism to further reduce the inference overhead. Extensive experiments on multiple benchmark datasets demonstrate that our method outperforms state-of-the-art KV cache quantization approaches in both efficiency and effectiveness.

MADLLM: Multivariate Anomaly Detection via Pre-trained LLMs

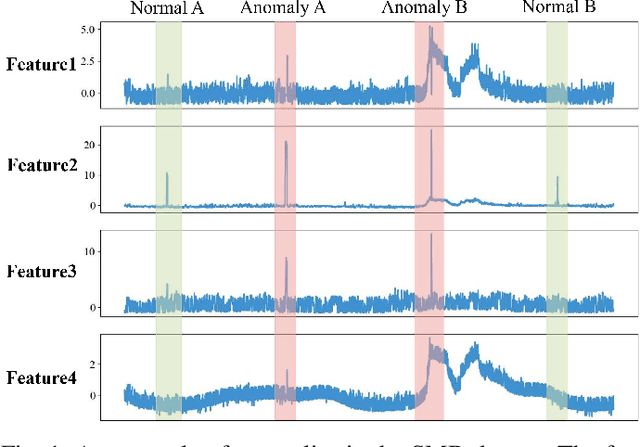
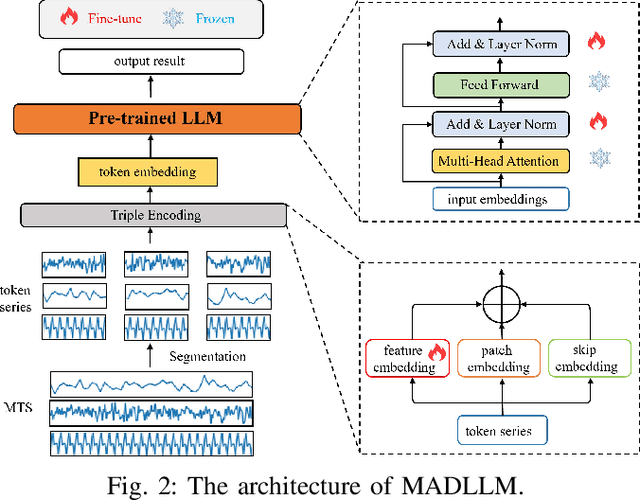
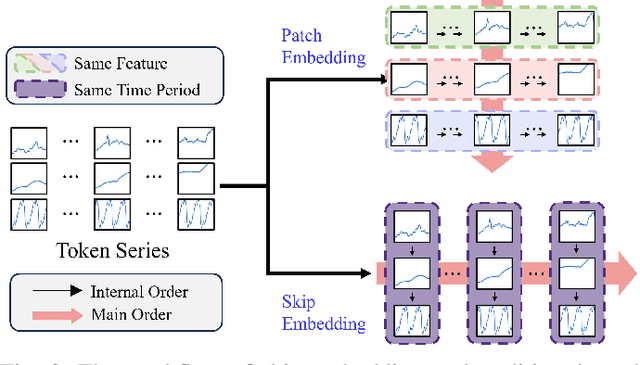
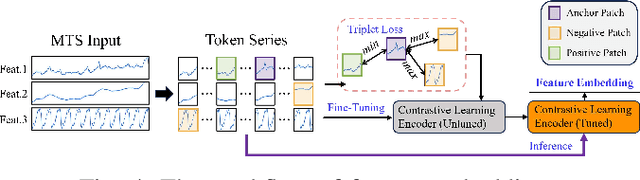
When applying pre-trained large language models (LLMs) to address anomaly detection tasks, the multivariate time series (MTS) modality of anomaly detection does not align with the text modality of LLMs. Existing methods simply transform the MTS data into multiple univariate time series sequences, which can cause many problems. This paper introduces MADLLM, a novel multivariate anomaly detection method via pre-trained LLMs. We design a new triple encoding technique to align the MTS modality with the text modality of LLMs. Specifically, this technique integrates the traditional patch embedding method with two novel embedding approaches: Skip Embedding, which alters the order of patch processing in traditional methods to help LLMs retain knowledge of previous features, and Feature Embedding, which leverages contrastive learning to allow the model to better understand the correlations between different features. Experimental results demonstrate that our method outperforms state-of-the-art methods in various public anomaly detection datasets.

Cocktail: Chunk-Adaptive Mixed-Precision Quantization for Long-Context LLM Inference

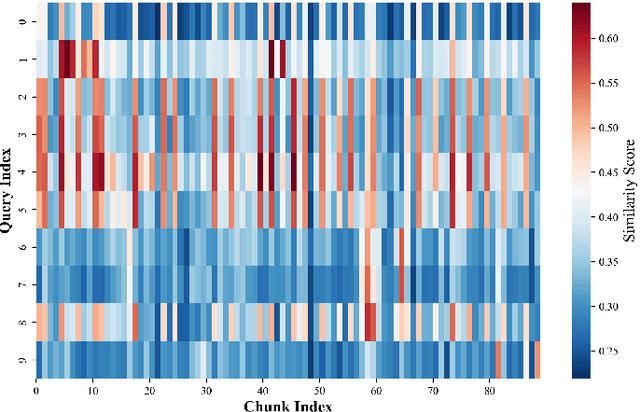
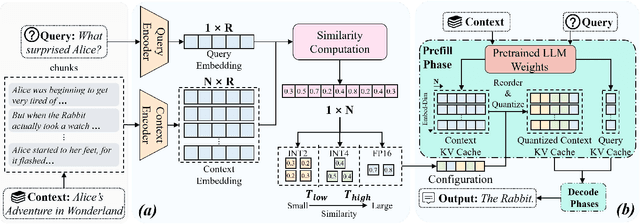
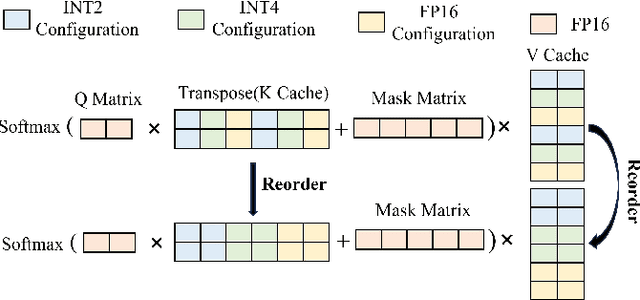
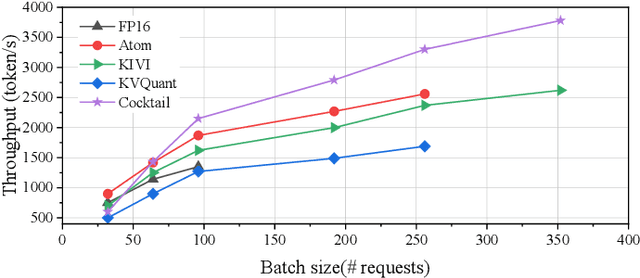
Recently, large language models (LLMs) have been able to handle longer and longer contexts. However, a context that is too long may cause intolerant inference latency and GPU memory usage. Existing methods propose mixed-precision quantization to the key-value (KV) cache in LLMs based on token granularity, which is time-consuming in the search process and hardware inefficient during computation. This paper introduces a novel approach called Cocktail, which employs chunk-adaptive mixed-precision quantization to optimize the KV cache. Cocktail consists of two modules: chunk-level quantization search and chunk-level KV cache computation. Chunk-level quantization search determines the optimal bitwidth configuration of the KV cache chunks quickly based on the similarity scores between the corresponding context chunks and the query, maintaining the model accuracy. Furthermore, chunk-level KV cache computation reorders the KV cache chunks before quantization, avoiding the hardware inefficiency caused by mixed-precision quantization in inference computation. Extensive experiments demonstrate that Cocktail outperforms state-of-the-art KV cache quantization methods on various models and datasets.

Dedicated Inference Engine and Binary-Weight Neural Networks for Lightweight Instance Segmentation

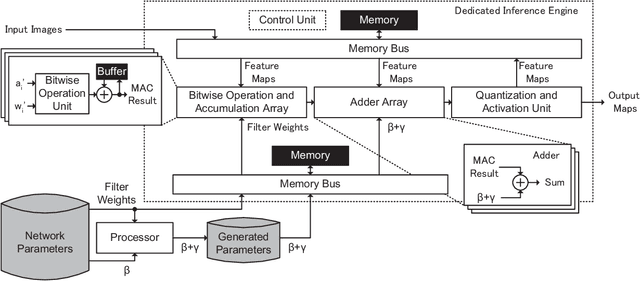
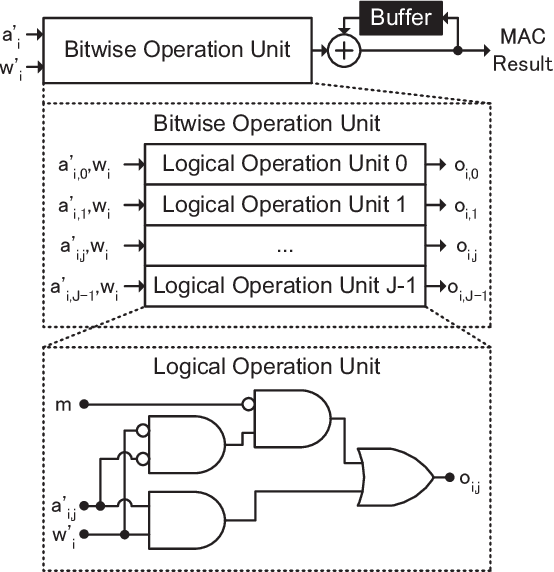
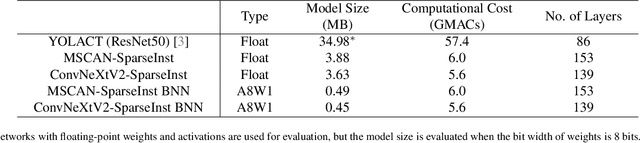
Reducing computational costs is an important issue for development of embedded systems. Binary-weight Neural Networks (BNNs), in which weights are binarized and activations are quantized, are employed to reduce computational costs of various kinds of applications. In this paper, a design methodology of hardware architecture for inference engines is proposed to handle modern BNNs with two operation modes. Multiply-Accumulate (MAC) operations can be simplified by replacing multiply operations with bitwise operations. The proposed method can effectively reduce the gate count of inference engines by removing a part of computational costs from the hardware system. The architecture of MAC operations can calculate the inference results of BNNs efficiently with only 52% of hardware costs compared with the related works. To show that the inference engine can handle practical applications, two lightweight networks which combine the backbones of SegNeXt and the decoder of SparseInst for instance segmentation are also proposed. The output results of the lightweight networks are computed using only bitwise operations and add operations. The proposed inference engine has lower hardware costs than related works. The experimental results show that the proposed inference engine can handle the proposed instance-segmentation networks and achieves higher accuracy than YOLACT on the "Person" category although the model size is 77.7$\times$ smaller compared with YOLACT.

UNet--: Memory-Efficient and Feature-Enhanced Network Architecture based on U-Net with Reduced Skip-Connections

U-Net models with encoder, decoder, and skip-connections components have demonstrated effectiveness in a variety of vision tasks. The skip-connections transmit fine-grained information from the encoder to the decoder. It is necessary to maintain the feature maps used by the skip-connections in memory before the decoding stage. Therefore, they are not friendly to devices with limited resource. In this paper, we propose a universal method and architecture to reduce the memory consumption and meanwhile generate enhanced feature maps to improve network performance. To this end, we design a simple but effective Multi-Scale Information Aggregation Module (MSIAM) in the encoder and an Information Enhancement Module (IEM) in the decoder. The MSIAM aggregates multi-scale feature maps into single-scale with less memory. After that, the aggregated feature maps can be expanded and enhanced to multi-scale feature maps by the IEM. By applying the proposed method on NAFNet, a SOTA model in the field of image restoration, we design a memory-efficient and feature-enhanced network architecture, UNet--. The memory demand by the skip-connections in the UNet-- is reduced by 93.3%, while the performance is improved compared to NAFNet. Furthermore, we show that our proposed method can be generalized to multiple visual tasks, with consistent improvements in both memory consumption and network accuracy compared to the existing efficient architectures.

MAGIS: LLM-Based Multi-Agent Framework for GitHub Issue Resolution

In software evolution, resolving the emergent issues within GitHub repositories is a complex challenge that involves not only the incorporation of new code but also the maintenance of existing functionalities. Large Language Models (LLMs) have shown promise in code generation and understanding but face difficulties in code change, particularly at the repository level. To overcome these challenges, we empirically study the reason why LLMs mostly fail to resolve GitHub issues and analyze some impact factors. Motivated by the empirical findings, we propose a novel LLM-based Multi-Agent framework for GitHub Issue reSolution, MAGIS, consisting of four kinds of agents customized for the software evolution: Manager, Repository Custodian, Developer, and Quality Assurance Engineer agents. This framework leverages the collaboration of various agents in the planning and coding process to unlock the potential of LLMs to resolve GitHub issues. In experiments, we employ the SWE-bench benchmark to compare MAGIS with popular LLMs, including GPT-3.5, GPT-4, and Claude-2. MAGIS can resolve 13.94% GitHub issues, which significantly outperforms the baselines. Specifically, MAGIS achieves an eight-fold increase in resolved ratio over the direct application of GPT-4, the based LLM of our method. We also analyze the factors for improving GitHub issue resolution rates, such as line location, task allocation, etc.

Data Interpreter: An LLM Agent For Data Science

Large Language Model (LLM)-based agents have demonstrated remarkable effectiveness. However, their performance can be compromised in data science scenarios that require real-time data adjustment, expertise in optimization due to complex dependencies among various tasks, and the ability to identify logical errors for precise reasoning. In this study, we introduce the Data Interpreter, a solution designed to solve with code that emphasizes three pivotal techniques to augment problem-solving in data science: 1) dynamic planning with hierarchical graph structures for real-time data adaptability;2) tool integration dynamically to enhance code proficiency during execution, enriching the requisite expertise;3) logical inconsistency identification in feedback, and efficiency enhancement through experience recording. We evaluate the Data Interpreter on various data science and real-world tasks. Compared to open-source baselines, it demonstrated superior performance, exhibiting significant improvements in machine learning tasks, increasing from 0.86 to 0.95. Additionally, it showed a 26% increase in the MATH dataset and a remarkable 112% improvement in open-ended tasks. The solution will be released at https://github.com/geekan/MetaGPT.

Value-Driven Mixed-Precision Quantization for Patch-Based Inference on Microcontrollers

Deploying neural networks on microcontroller units (MCUs) presents substantial challenges due to their constrained computation and memory resources. Previous researches have explored patch-based inference as a strategy to conserve memory without sacrificing model accuracy. However, this technique suffers from severe redundant computation overhead, leading to a substantial increase in execution latency. A feasible solution to address this issue is mixed-precision quantization, but it faces the challenges of accuracy degradation and a time-consuming search time. In this paper, we propose QuantMCU, a novel patch-based inference method that utilizes value-driven mixed-precision quantization to reduce redundant computation. We first utilize value-driven patch classification (VDPC) to maintain the model accuracy. VDPC classifies patches into two classes based on whether they contain outlier values. For patches containing outlier values, we apply 8-bit quantization to the feature maps on the dataflow branches that follow. In addition, for patches without outlier values, we utilize value-driven quantization search (VDQS) on the feature maps of their following dataflow branches to reduce search time. Specifically, VDQS introduces a novel quantization search metric that takes into account both computation and accuracy, and it employs entropy as an accuracy representation to avoid additional training. VDQS also adopts an iterative approach to determine the bitwidth of each feature map to further accelerate the search process. Experimental results on real-world MCU devices show that QuantMCU can reduce computation by 2.2x on average while maintaining comparable model accuracy compared to the state-of-the-art patch-based inference methods.

KADEL: Knowledge-Aware Denoising Learning for Commit Message Generation

Commit messages are natural language descriptions of code changes, which are important for software evolution such as code understanding and maintenance. However, previous methods are trained on the entire dataset without considering the fact that a portion of commit messages adhere to good practice (i.e., good-practice commits), while the rest do not. On the basis of our empirical study, we discover that training on good-practice commits significantly contributes to the commit message generation. Motivated by this finding, we propose a novel knowledge-aware denoising learning method called KADEL. Considering that good-practice commits constitute only a small proportion of the dataset, we align the remaining training samples with these good-practice commits. To achieve this, we propose a model that learns the commit knowledge by training on good-practice commits. This knowledge model enables supplementing more information for training samples that do not conform to good practice. However, since the supplementary information may contain noise or prediction errors, we propose a dynamic denoising training method. This method composes a distribution-aware confidence function and a dynamic distribution list, which enhances the effectiveness of the training process. Experimental results on the whole MCMD dataset demonstrate that our method overall achieves state-of-the-art performance compared with previous methods. Our source code and data are available at https://github.com/DeepSoftwareAnalytics/KADEL