Guideline for Trustworthy Artificial Intelligence -- AI Assessment Catalog

Artificial Intelligence (AI) has made impressive progress in recent years and represents a key technology that has a crucial impact on the economy and society. However, it is clear that AI and business models based on it can only reach their full potential if AI applications are developed according to high quality standards and are effectively protected against new AI risks. For instance, AI bears the risk of unfair treatment of individuals when processing personal data e.g., to support credit lending or staff recruitment decisions. The emergence of these new risks is closely linked to the fact that the behavior of AI applications, particularly those based on Machine Learning (ML), is essentially learned from large volumes of data and is not predetermined by fixed programmed rules. Thus, the issue of the trustworthiness of AI applications is crucial and is the subject of numerous major publications by stakeholders in politics, business and society. In addition, there is mutual agreement that the requirements for trustworthy AI, which are often described in an abstract way, must now be made clear and tangible. One challenge to overcome here relates to the fact that the specific quality criteria for an AI application depend heavily on the application context and possible measures to fulfill them in turn depend heavily on the AI technology used. Lastly, practical assessment procedures are needed to evaluate whether specific AI applications have been developed according to adequate quality standards. This AI assessment catalog addresses exactly this point and is intended for two target groups: Firstly, it provides developers with a guideline for systematically making their AI applications trustworthy. Secondly, it guides assessors and auditors on how to examine AI applications for trustworthiness in a structured way.

Robustness in Fatigue Strength Estimation

Fatigue strength estimation is a costly manual material characterization process in which state-of-the-art approaches follow a standardized experiment and analysis procedure. In this paper, we examine a modular, Machine Learning-based approach for fatigue strength estimation that is likely to reduce the number of experiments and, thus, the overall experimental costs. Despite its high potential, deployment of a new approach in a real-life lab requires more than the theoretical definition and simulation. Therefore, we study the robustness of the approach against misspecification of the prior and discretization of the specified loads. We identify its applicability and its advantageous behavior over the state-of-the-art methods, potentially reducing the number of costly experiments.

Multi-Agent Neural Rewriter for Vehicle Routing with Limited Disclosure of Costs

We interpret solving the multi-vehicle routing problem as a team Markov game with partially observable costs. For a given set of customers to serve, the playing agents (vehicles) have the common goal to determine the team-optimal agent routes with minimal total cost. Each agent thereby observes only its own cost. Our multi-agent reinforcement learning approach, the so-called multi-agent Neural Rewriter, builds on the single-agent Neural Rewriter to solve the problem by iteratively rewriting solutions. Parallel agent action execution and partial observability require new rewriting rules for the game. We propose the introduction of a so-called pool in the system which serves as a collection point for unvisited nodes. It enables agents to act simultaneously and exchange nodes in a conflict-free manner. We realize limited disclosure of agent-specific costs by only sharing them during learning. During inference, each agents acts decentrally, solely based on its own cost. First empirical results on small problem sizes demonstrate that we reach a performance close to the employed OR-Tools benchmark which operates in the perfect cost information setting.

Tailored Uncertainty Estimation for Deep Learning Systems

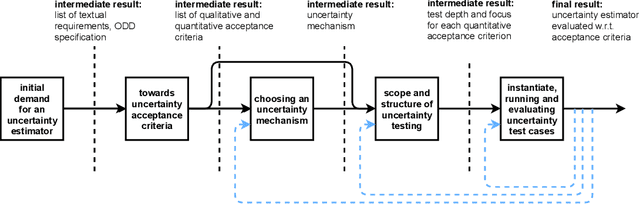
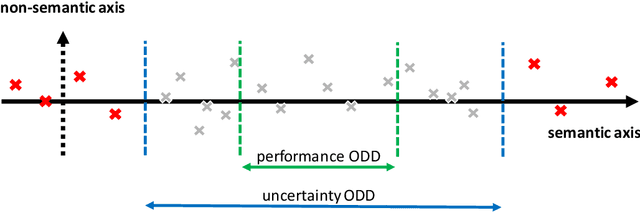
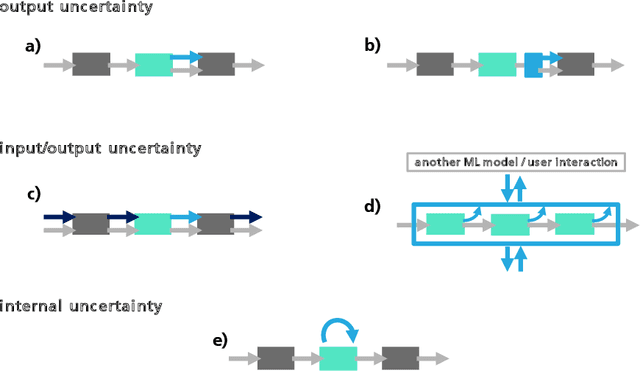
Uncertainty estimation bears the potential to make deep learning (DL) systems more reliable. Standard techniques for uncertainty estimation, however, come along with specific combinations of strengths and weaknesses, e.g., with respect to estimation quality, generalization abilities and computational complexity. To actually harness the potential of uncertainty quantification, estimators are required whose properties closely match the requirements of a given use case. In this work, we propose a framework that, firstly, structures and shapes these requirements, secondly, guides the selection of a suitable uncertainty estimation method and, thirdly, provides strategies to validate this choice and to uncover structural weaknesses. By contributing tailored uncertainty estimation in this sense, our framework helps to foster trustworthy DL systems. Moreover, it anticipates prospective machine learning regulations that require, e.g., in the EU, evidences for the technical appropriateness of machine learning systems. Our framework provides such evidences for system components modeling uncertainty.

Graph Filtration Kernels

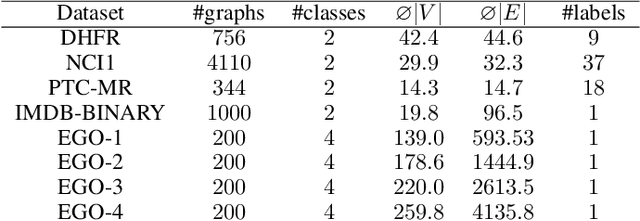
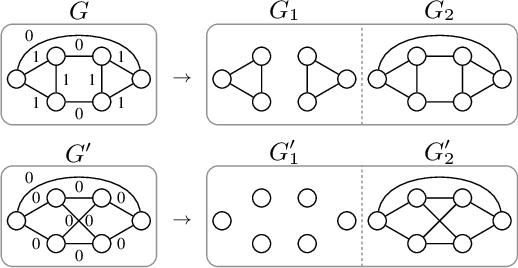
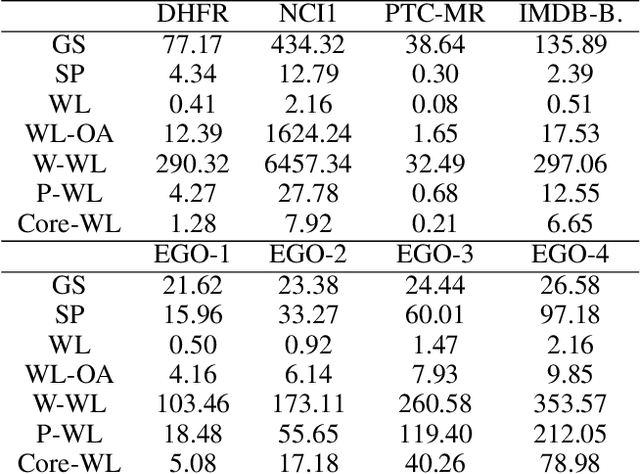
The majority of popular graph kernels is based on the concept of Haussler's $\mathcal{R}$-convolution kernel and defines graph similarities in terms of mutual substructures. In this work, we enrich these similarity measures by considering graph filtrations: Using meaningful orders on the set of edges, which allow to construct a sequence of nested graphs, we can consider a graph at multiple granularities. For one thing, this provides access to features on different levels of resolution. Furthermore, rather than to simply compare frequencies of features in graphs, it allows for their comparison in terms of when and for how long they exist in the sequences. In this work, we propose a family of graph kernels that incorporate these existence intervals of features. While our approach can be applied to arbitrary graph features, we particularly highlight Weisfeiler-Lehman vertex labels, leading to efficient kernels. We show that using Weisfeiler-Lehman labels over certain filtrations strictly increases the expressive power over the ordinary Weisfeiler-Lehman procedure in terms of deciding graph isomorphism. In fact, this result directly yields more powerful graph kernels based on such features and has implications to graph neural networks due to their close relationship to the Weisfeiler-Lehman method. We empirically validate the expressive power of our graph kernels and show significant improvements over state-of-the-art graph kernels in terms of predictive performance on various real-world benchmark datasets.

Learning Weakly Convex Sets in Metric Spaces

We introduce the notion of weak convexity in metric spaces, a generalization of ordinary convexity commonly used in machine learning. It is shown that weakly convex sets can be characterized by a closure operator and have a unique decomposition into a set of pairwise disjoint connected blocks. We give two generic efficient algorithms, an extensional and an intensional one for learning weakly convex concepts and study their formal properties. Our experimental results concerning vertex classification clearly demonstrate the excellent predictive performance of the extensional algorithm. Two non-trivial applications of the intensional algorithm to polynomial PAC-learnability are presented. The first one deals with learning $k$-convex Boolean functions, which are already known to be efficiently PAC-learnable. It is shown how to derive this positive result in a fairly easy way by the generic intensional algorithm. The second one is concerned with the Euclidean space equipped with the Manhattan distance. For this metric space, weakly convex sets are a union of pairwise disjoint axis-aligned hyperrectangles. We show that a weakly convex set that is consistent with a set of examples and contains a minimum number of hyperrectangles can be found in polynomial time. In contrast, this problem is known to be NP-complete if the hyperrectangles may be overlapping.

A Generalized Weisfeiler-Lehman Graph Kernel

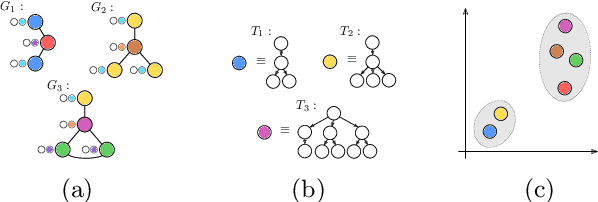
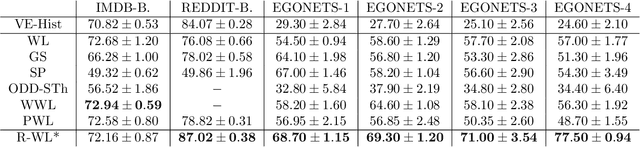
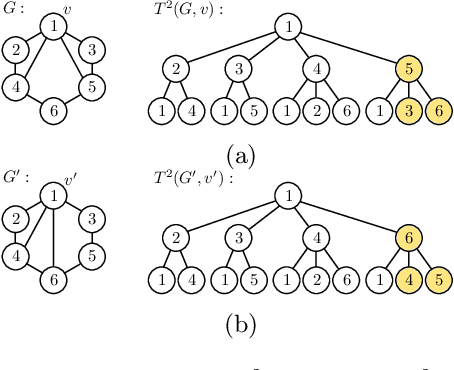
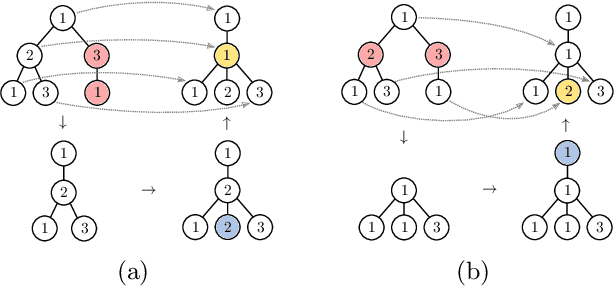
The Weisfeiler-Lehman graph kernels are among the most prevalent graph kernels due to their remarkable time complexity and predictive performance. Their key concept is based on an implicit comparison of neighborhood representing trees with respect to equality (i.e., isomorphism). This binary valued comparison is, however, arguably too rigid for defining suitable similarity measures over graphs. To overcome this limitation, we propose a generalization of Weisfeiler-Lehman graph kernels which takes into account the similarity between trees rather than equality. We achieve this using a specifically fitted variation of the well-known tree edit distance which can efficiently be calculated. We empirically show that our approach significantly outperforms state-of-the-art methods in terms of predictive performance on datasets containing structurally more complex graphs beyond the typically considered molecular graphs.

A Novel Regression Loss for Non-Parametric Uncertainty Optimization

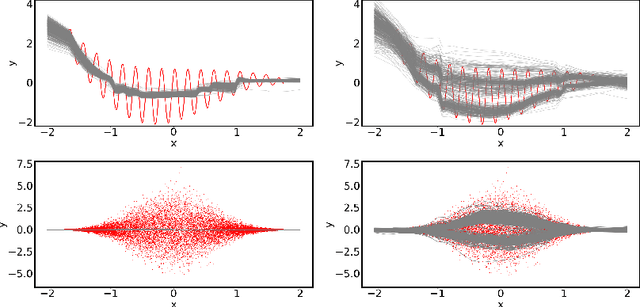
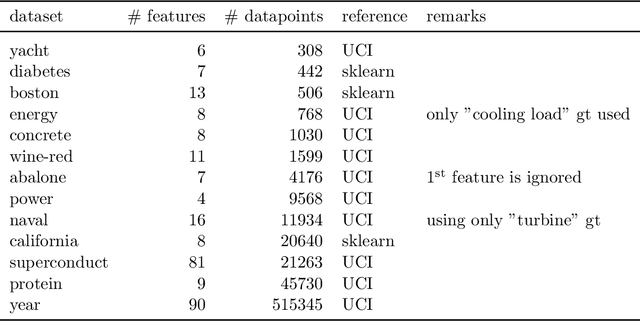
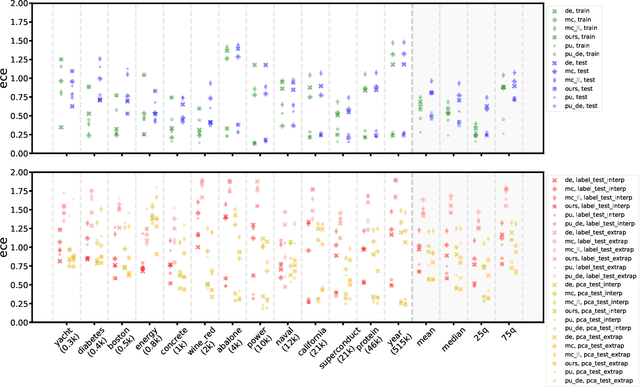
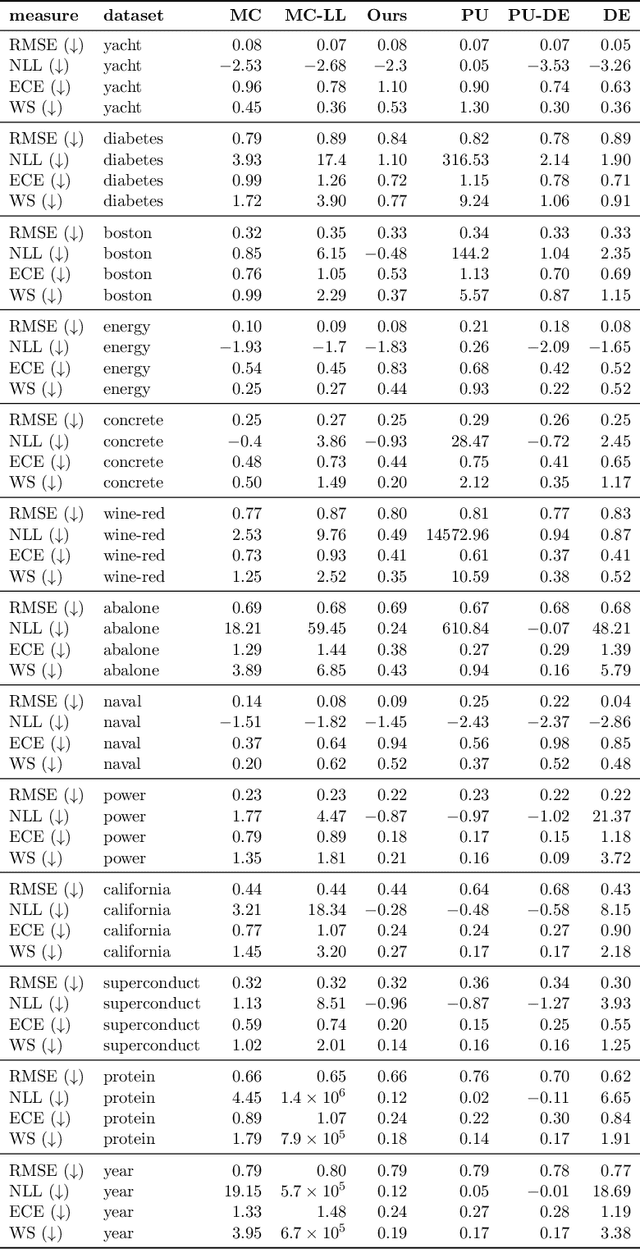
Quantification of uncertainty is one of the most promising approaches to establish safe machine learning. Despite its importance, it is far from being generally solved, especially for neural networks. One of the most commonly used approaches so far is Monte Carlo dropout, which is computationally cheap and easy to apply in practice. However, it can underestimate the uncertainty. We propose a new objective, referred to as second-moment loss (SML), to address this issue. While the full network is encouraged to model the mean, the dropout networks are explicitly used to optimize the model variance. We intensively study the performance of the new objective on various UCI regression datasets. Comparing to the state-of-the-art of deep ensembles, SML leads to comparable prediction accuracies and uncertainty estimates while only requiring a single model. Under distribution shift, we observe moderate improvements. As a side result, we introduce an intuitive Wasserstein distance-based uncertainty measure that is non-saturating and thus allows to resolve quality differences between any two uncertainty estimates.

Second-Moment Loss: A Novel Regression Objective for Improved Uncertainties

Quantification of uncertainty is one of the most promising approaches to establish safe machine learning. Despite its importance, it is far from being generally solved, especially for neural networks. One of the most commonly used approaches so far is Monte Carlo dropout, which is computationally cheap and easy to apply in practice. However, it can underestimate the uncertainty. We propose a new objective, referred to as second-moment loss (SML), to address this issue. While the full network is encouraged to model the mean, the dropout networks are explicitly used to optimize the model variance. We analyze the performance of the new objective on various toy and UCI regression datasets. Comparing to the state-of-the-art of deep ensembles, SML leads to comparable prediction accuracies and uncertainty estimates while only requiring a single model. Under distribution shift, we observe moderate improvements. From a safety perspective also the study of worst-case uncertainties is crucial. In this regard we improve considerably. Finally, we show that SML can be successfully applied to SqueezeDet, a modern object detection network. We improve on its uncertainty-related scores while not deteriorating regression quality. As a side result, we introduce an intuitive Wasserstein distance-based uncertainty measure that is non-saturating and thus allows to resolve quality differences between any two uncertainty estimates.

Learning Syllogism with Euler Neural-Networks

Traditional neural networks represent everything as a vector, and are able to approximate a subset of logical reasoning to a certain degree. As basic logic relations are better represented by topological relations between regions, we propose a novel neural network that represents everything as a ball and is able to learn topological configuration as an Euler diagram. So comes the name Euler Neural-Network (ENN). The central vector of a ball is a vector that can inherit representation power of traditional neural network. ENN distinguishes four spatial statuses between balls, namely, being disconnected, being partially overlapped, being part of, being inverse part of. Within each status, ideal values are defined for efficient reasoning. A novel back-propagation algorithm with six Rectified Spatial Units (ReSU) can optimize an Euler diagram representing logical premises, from which logical conclusion can be deduced. In contrast to traditional neural network, ENN can precisely represent all 24 different structures of Syllogism. Two large datasets are created: one extracted from WordNet-3.0 covers all types of Syllogism reasoning, the other extracted all family relations from DBpedia. Experiment results approve the superior power of ENN in logical representation and reasoning. Datasets and source code are available upon request.