Beyond Shallow Heuristics: Leveraging Human Intuition for Curriculum Learning

Curriculum learning (CL) aims to improve training by presenting data from "easy" to "hard", yet defining and measuring linguistic difficulty remains an open challenge. We investigate whether human-curated simple language can serve as an effective signal for CL. Using the article-level labels from the Simple Wikipedia corpus, we compare label-based curricula to competence-based strategies relying on shallow heuristics. Our experiments with a BERT-tiny model show that adding simple data alone yields no clear benefit. However, structuring it via a curriculum -- especially when introduced first -- consistently improves perplexity, particularly on simple language. In contrast, competence-based curricula lead to no consistent gains over random ordering, probably because they fail to effectively separate the two classes. Our results suggest that human intuition about linguistic difficulty can guide CL for language model pre-training.

CFIRE: A General Method for Combining Local Explanations

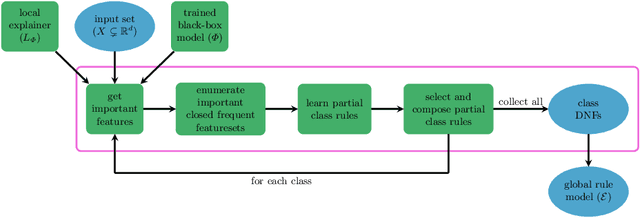
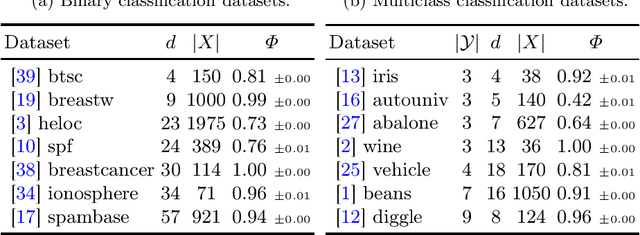
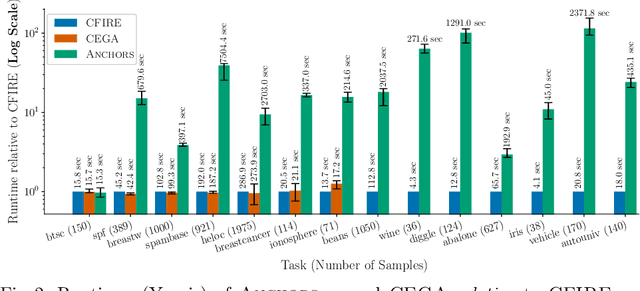
We propose a novel eXplainable AI algorithm to compute faithful, easy-to-understand, and complete global decision rules from local explanations for tabular data by combining XAI methods with closed frequent itemset mining. Our method can be used with any local explainer that indicates which dimensions are important for a given sample for a given black-box decision. This property allows our algorithm to choose among different local explainers, addressing the disagreement problem, \ie the observation that no single explanation method consistently outperforms others across models and datasets. Unlike usual experimental methodology, our evaluation also accounts for the Rashomon effect in model explainability. To this end, we demonstrate the robustness of our approach in finding suitable rules for nearly all of the 700 black-box models we considered across 14 benchmark datasets. The results also show that our method exhibits improved runtime, high precision and F1-score while generating compact and complete rules.

Iterative Graph Neural Network Enhancement via Frequent Subgraph Mining of Explanations

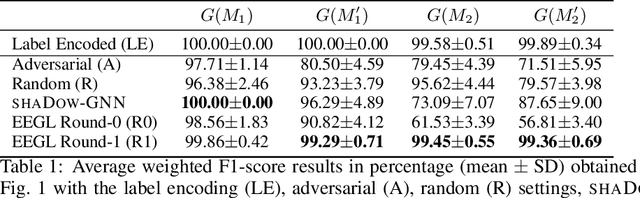
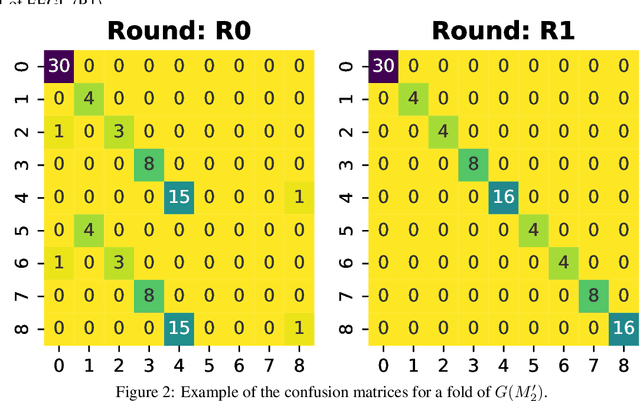
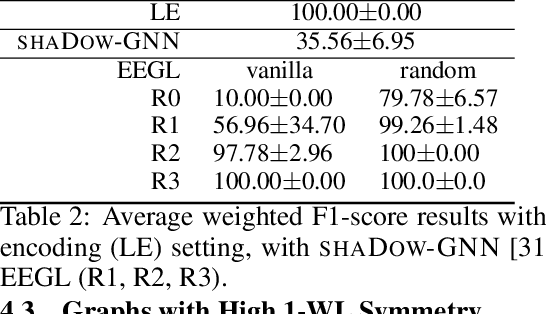
We formulate an XAI-based model improvement approach for Graph Neural Networks (GNNs) for node classification, called Explanation Enhanced Graph Learning (EEGL). The goal is to improve predictive performance of GNN using explanations. EEGL is an iterative self-improving algorithm, which starts with a learned "vanilla" GNN, and repeatedly uses frequent subgraph mining to find relevant patterns in explanation subgraphs. These patterns are then filtered further to obtain application-dependent features corresponding to the presence of certain subgraphs in the node neighborhoods. Giving an application-dependent algorithm for such a subgraph-based extension of the Weisfeiler-Leman (1-WL) algorithm has previously been posed as an open problem. We present experimental evidence, with synthetic and real-world data, which show that EEGL outperforms related approaches in predictive performance and that it has a node-distinguishing power beyond that of vanilla GNNs. We also analyze EEGL's training dynamics.

Learning Weakly Convex Sets in Metric Spaces

We introduce the notion of weak convexity in metric spaces, a generalization of ordinary convexity commonly used in machine learning. It is shown that weakly convex sets can be characterized by a closure operator and have a unique decomposition into a set of pairwise disjoint connected blocks. We give two generic efficient algorithms, an extensional and an intensional one for learning weakly convex concepts and study their formal properties. Our experimental results concerning vertex classification clearly demonstrate the excellent predictive performance of the extensional algorithm. Two non-trivial applications of the intensional algorithm to polynomial PAC-learnability are presented. The first one deals with learning $k$-convex Boolean functions, which are already known to be efficiently PAC-learnable. It is shown how to derive this positive result in a fairly easy way by the generic intensional algorithm. The second one is concerned with the Euclidean space equipped with the Manhattan distance. For this metric space, weakly convex sets are a union of pairwise disjoint axis-aligned hyperrectangles. We show that a weakly convex set that is consistent with a set of examples and contains a minimum number of hyperrectangles can be found in polynomial time. In contrast, this problem is known to be NP-complete if the hyperrectangles may be overlapping.

A Generalized Weisfeiler-Lehman Graph Kernel

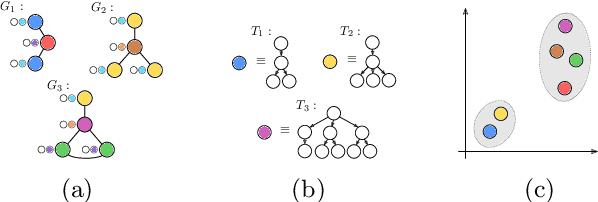
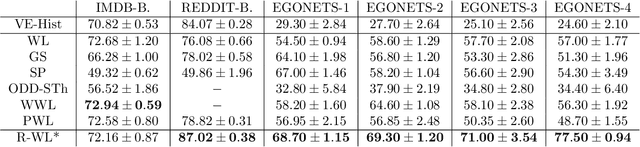
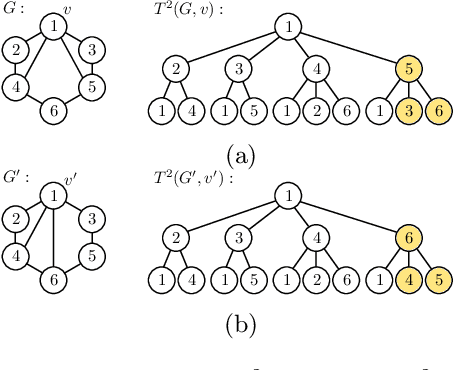
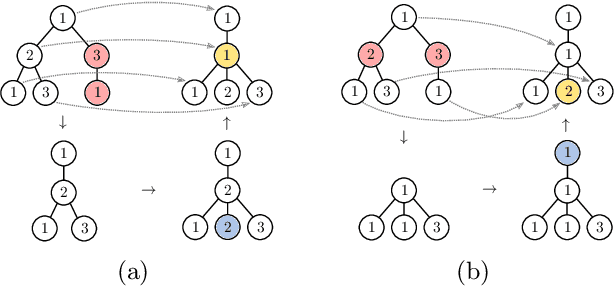
The Weisfeiler-Lehman graph kernels are among the most prevalent graph kernels due to their remarkable time complexity and predictive performance. Their key concept is based on an implicit comparison of neighborhood representing trees with respect to equality (i.e., isomorphism). This binary valued comparison is, however, arguably too rigid for defining suitable similarity measures over graphs. To overcome this limitation, we propose a generalization of Weisfeiler-Lehman graph kernels which takes into account the similarity between trees rather than equality. We achieve this using a specifically fitted variation of the well-known tree edit distance which can efficiently be calculated. We empirically show that our approach significantly outperforms state-of-the-art methods in terms of predictive performance on datasets containing structurally more complex graphs beyond the typically considered molecular graphs.