Learning Long Range Dependencies on Graphs via Random Walks

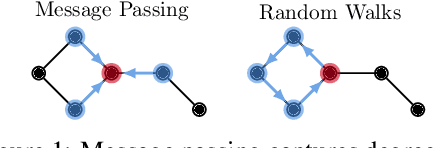
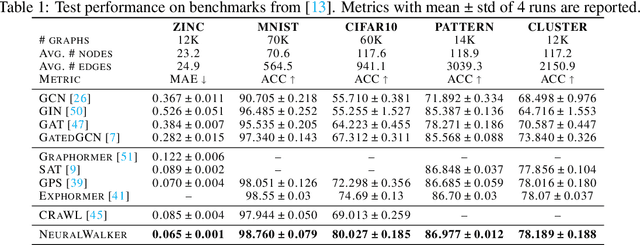
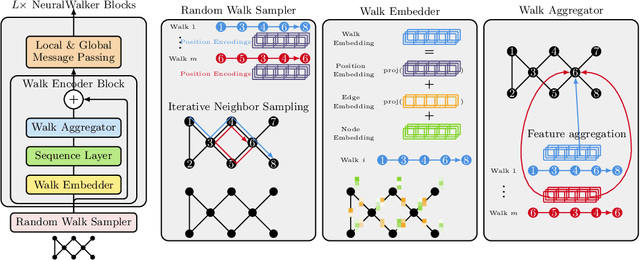
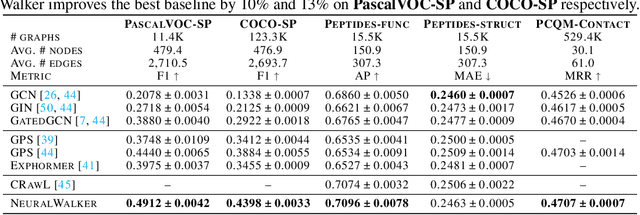
Message-passing graph neural networks (GNNs), while excelling at capturing local relationships, often struggle with long-range dependencies on graphs. Conversely, graph transformers (GTs) enable information exchange between all nodes but oversimplify the graph structure by treating them as a set of fixed-length vectors. This work proposes a novel architecture, NeuralWalker, that overcomes the limitations of both methods by combining random walks with message passing. NeuralWalker achieves this by treating random walks as sequences, allowing for the application of recent advances in sequence models in order to capture long-range dependencies within these walks. Based on this concept, we propose a framework that offers (1) more expressive graph representations through random walk sequences, (2) the ability to utilize any sequence model for capturing long-range dependencies, and (3) the flexibility by integrating various GNN and GT architectures. Our experimental evaluations demonstrate that NeuralWalker achieves significant performance improvements on 19 graph and node benchmark datasets, notably outperforming existing methods by up to 13% on the PascalVoc-SP and COCO-SP datasets. Code is available at https://github.com/BorgwardtLab/NeuralWalker.

Graph Filtration Kernels

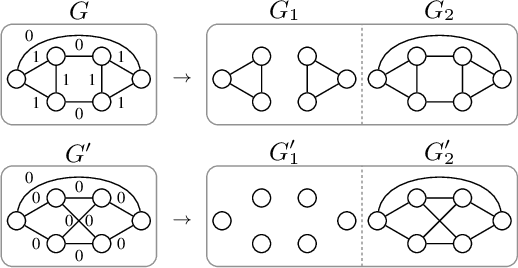
The majority of popular graph kernels is based on the concept of Haussler's $\mathcal{R}$-convolution kernel and defines graph similarities in terms of mutual substructures. In this work, we enrich these similarity measures by considering graph filtrations: Using meaningful orders on the set of edges, which allow to construct a sequence of nested graphs, we can consider a graph at multiple granularities. For one thing, this provides access to features on different levels of resolution. Furthermore, rather than to simply compare frequencies of features in graphs, it allows for their comparison in terms of when and for how long they exist in the sequences. In this work, we propose a family of graph kernels that incorporate these existence intervals of features. While our approach can be applied to arbitrary graph features, we particularly highlight Weisfeiler-Lehman vertex labels, leading to efficient kernels. We show that using Weisfeiler-Lehman labels over certain filtrations strictly increases the expressive power over the ordinary Weisfeiler-Lehman procedure in terms of deciding graph isomorphism. In fact, this result directly yields more powerful graph kernels based on such features and has implications to graph neural networks due to their close relationship to the Weisfeiler-Lehman method. We empirically validate the expressive power of our graph kernels and show significant improvements over state-of-the-art graph kernels in terms of predictive performance on various real-world benchmark datasets.

A Generalized Weisfeiler-Lehman Graph Kernel

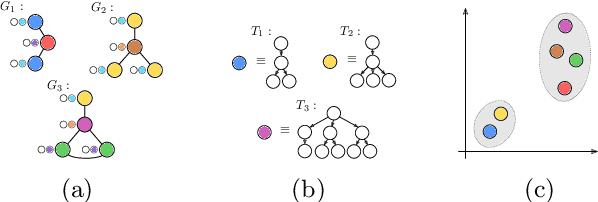
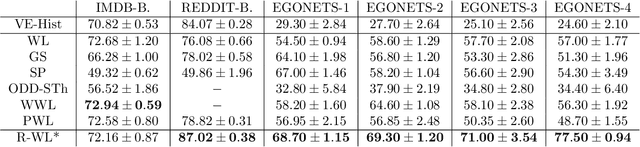
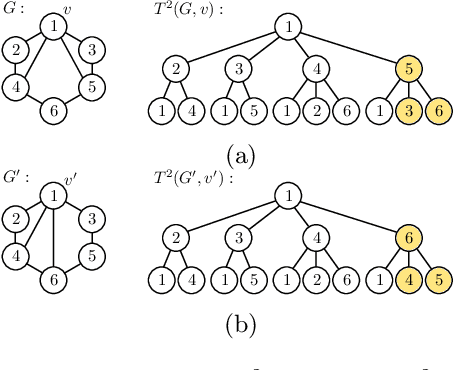
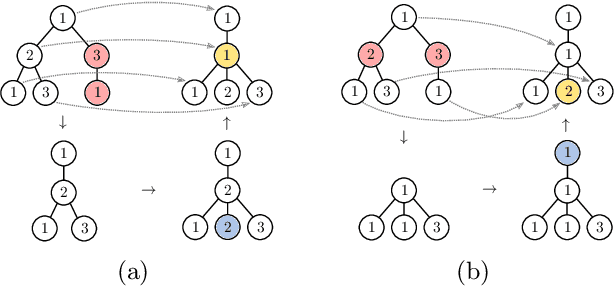
The Weisfeiler-Lehman graph kernels are among the most prevalent graph kernels due to their remarkable time complexity and predictive performance. Their key concept is based on an implicit comparison of neighborhood representing trees with respect to equality (i.e., isomorphism). This binary valued comparison is, however, arguably too rigid for defining suitable similarity measures over graphs. To overcome this limitation, we propose a generalization of Weisfeiler-Lehman graph kernels which takes into account the similarity between trees rather than equality. We achieve this using a specifically fitted variation of the well-known tree edit distance which can efficiently be calculated. We empirically show that our approach significantly outperforms state-of-the-art methods in terms of predictive performance on datasets containing structurally more complex graphs beyond the typically considered molecular graphs.