Karsten Borgwardt
A Comprehensive Benchmark for RNA 3D Structure-Function Modeling
Mar 27, 2025


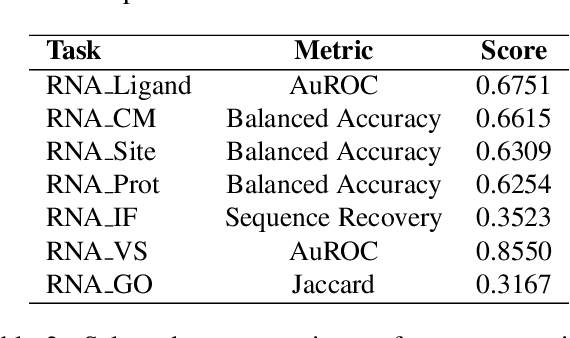
Abstract:The RNA structure-function relationship has recently garnered significant attention within the deep learning community, promising to grow in importance as nucleic acid structure models advance. However, the absence of standardized and accessible benchmarks for deep learning on RNA 3D structures has impeded the development of models for RNA functional characteristics. In this work, we introduce a set of seven benchmarking datasets for RNA structure-function prediction, designed to address this gap. Our library builds on the established Python library rnaglib, and offers easy data distribution and encoding, splitters and evaluation methods, providing a convenient all-in-one framework for comparing models. Datasets are implemented in a fully modular and reproducible manner, facilitating for community contributions and customization. Finally, we provide initial baseline results for all tasks using a graph neural network. Source code: https://github.com/cgoliver/rnaglib Documentation: https://rnaglib.org
Flatten Graphs as Sequences: Transformers are Scalable Graph Generators
Feb 04, 2025

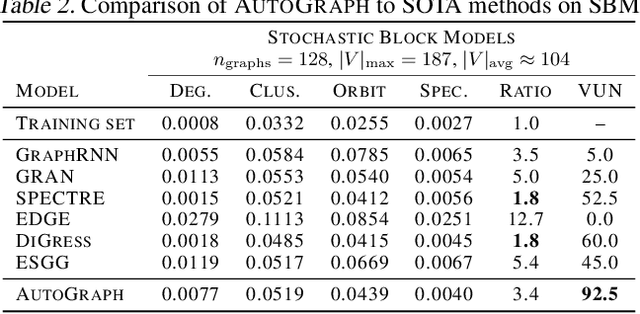

Abstract:We introduce AutoGraph, a novel autoregressive framework for generating large attributed graphs using decoder-only transformers. At the core of our approach is a reversible "flattening" process that transforms graphs into random sequences. By sampling and learning from these sequences, AutoGraph enables transformers to model and generate complex graph structures in a manner akin to natural language. In contrast to diffusion models that rely on computationally intensive node features, our approach operates exclusively on these sequences. The sampling complexity and sequence length scale linearly with the number of edges, making AutoGraph highly scalable for generating large sparse graphs. Empirically, AutoGraph achieves state-of-the-art performance across diverse synthetic and molecular graph generation benchmarks, while delivering a 100-fold generation and a 3-fold training speedup compared to leading diffusion models. Additionally, it demonstrates promising transfer capabilities and supports substructure-conditioned generation without additional fine-tuning. By extending language modeling techniques to graph generation, this work paves the way for developing graph foundation models.
Towards Fast Graph Generation via Autoregressive Noisy Filtration Modeling
Feb 04, 2025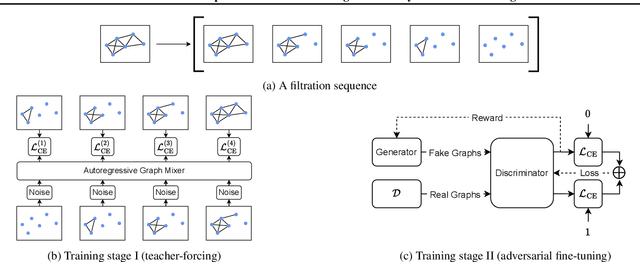


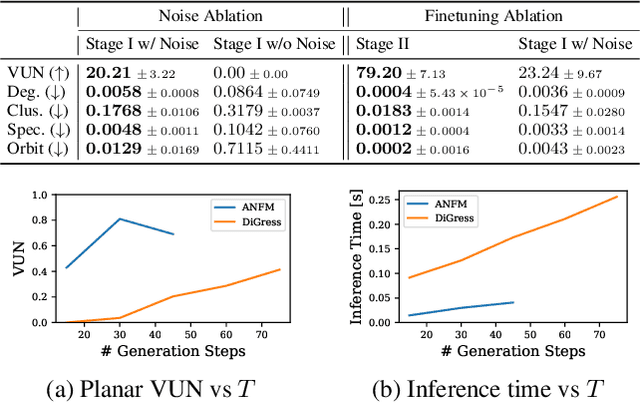
Abstract:Graph generative models often face a critical trade-off between learning complex distributions and achieving fast generation speed. We introduce Autoregressive Noisy Filtration Modeling (ANFM), a novel approach that addresses both challenges. ANFM leverages filtration, a concept from topological data analysis, to transform graphs into short sequences of monotonically increasing subgraphs. This formulation extends the sequence families used in previous autoregressive models. To learn from these sequences, we propose a novel autoregressive graph mixer model. Our experiments suggest that exposure bias might represent a substantial hurdle in autoregressive graph generation and we introduce two mitigation strategies to address it: noise augmentation and a reinforcement learning approach. Incorporating these techniques leads to substantial performance gains, making ANFM competitive with state-of-the-art diffusion models across diverse synthetic and real-world datasets. Notably, ANFM produces remarkably short sequences, achieving a 100-fold speedup in generation time compared to diffusion models. This work marks a significant step toward high-throughput graph generation.
Learning Long Range Dependencies on Graphs via Random Walks
Jun 05, 2024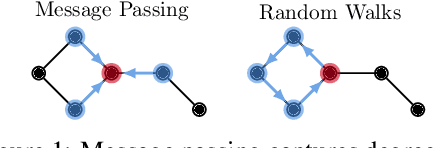
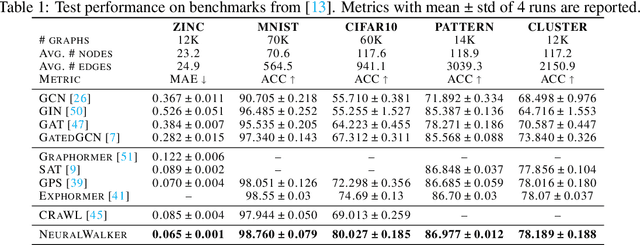
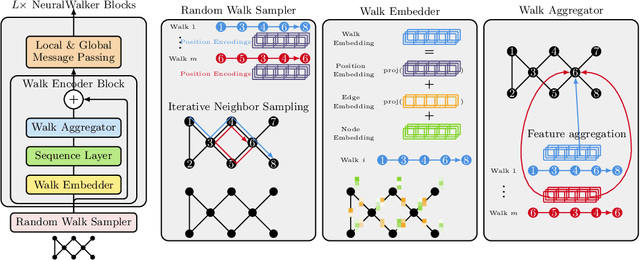
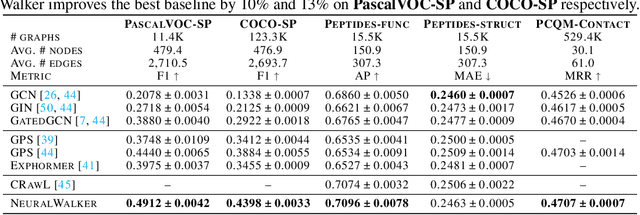
Abstract:Message-passing graph neural networks (GNNs), while excelling at capturing local relationships, often struggle with long-range dependencies on graphs. Conversely, graph transformers (GTs) enable information exchange between all nodes but oversimplify the graph structure by treating them as a set of fixed-length vectors. This work proposes a novel architecture, NeuralWalker, that overcomes the limitations of both methods by combining random walks with message passing. NeuralWalker achieves this by treating random walks as sequences, allowing for the application of recent advances in sequence models in order to capture long-range dependencies within these walks. Based on this concept, we propose a framework that offers (1) more expressive graph representations through random walk sequences, (2) the ability to utilize any sequence model for capturing long-range dependencies, and (3) the flexibility by integrating various GNN and GT architectures. Our experimental evaluations demonstrate that NeuralWalker achieves significant performance improvements on 19 graph and node benchmark datasets, notably outperforming existing methods by up to 13% on the PascalVoc-SP and COCO-SP datasets. Code is available at https://github.com/BorgwardtLab/NeuralWalker.
Endowing Protein Language Models with Structural Knowledge
Jan 26, 2024Abstract:Understanding the relationships between protein sequence, structure and function is a long-standing biological challenge with manifold implications from drug design to our understanding of evolution. Recently, protein language models have emerged as the preferred method for this challenge, thanks to their ability to harness large sequence databases. Yet, their reliance on expansive sequence data and parameter sets limits their flexibility and practicality in real-world scenarios. Concurrently, the recent surge in computationally predicted protein structures unlocks new opportunities in protein representation learning. While promising, the computational burden carried by such complex data still hinders widely-adopted practical applications. To address these limitations, we introduce a novel framework that enhances protein language models by integrating protein structural data. Drawing from recent advances in graph transformers, our approach refines the self-attention mechanisms of pretrained language transformers by integrating structural information with structure extractor modules. This refined model, termed Protein Structure Transformer (PST), is further pretrained on a small protein structure database, using the same masked language modeling objective as traditional protein language models. Empirical evaluations of PST demonstrate its superior parameter efficiency relative to protein language models, despite being pretrained on a dataset comprising only 542K structures. Notably, PST consistently outperforms the state-of-the-art foundation model for protein sequences, ESM-2, setting a new benchmark in protein function prediction. Our findings underscore the potential of integrating structural information into protein language models, paving the way for more effective and efficient protein modeling Code and pretrained models are available at https://github.com/BorgwardtLab/PST.
Fisher Information Embedding for Node and Graph Learning
May 12, 2023
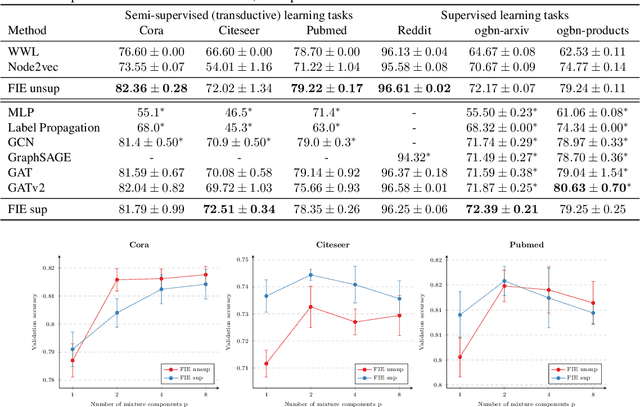
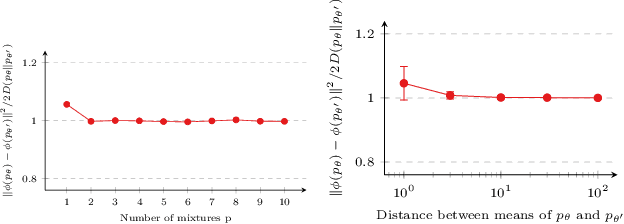
Abstract:Attention-based graph neural networks (GNNs), such as graph attention networks (GATs), have become popular neural architectures for processing graph-structured data and learning node embeddings. Despite their empirical success, these models rely on labeled data and the theoretical properties of these models have yet to be fully understood. In this work, we propose a novel attention-based node embedding framework for graphs. Our framework builds upon a hierarchical kernel for multisets of subgraphs around nodes (e.g. neighborhoods) and each kernel leverages the geometry of a smooth statistical manifold to compare pairs of multisets, by "projecting" the multisets onto the manifold. By explicitly computing node embeddings with a manifold of Gaussian mixtures, our method leads to a new attention mechanism for neighborhood aggregation. We provide theoretical insights into genralizability and expressivity of our embeddings, contributing to a deeper understanding of attention-based GNNs. We propose efficient unsupervised and supervised methods for learning the embeddings, with the unsupervised method not requiring any labeled data. Through experiments on several node classification benchmarks, we demonstrate that our proposed method outperforms existing attention-based graph models like GATs. Our code is available at https://github.com/BorgwardtLab/fisher_information_embedding.
Unsupervised Manifold Alignment with Joint Multidimensional Scaling
Jul 06, 2022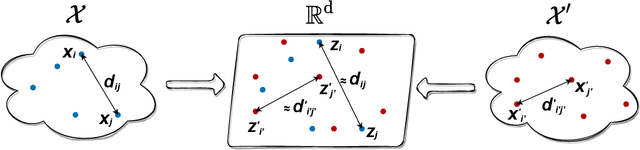
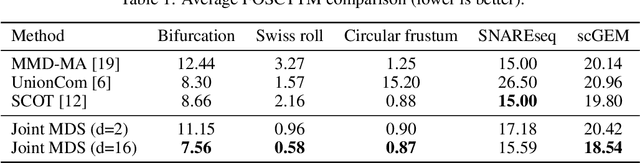
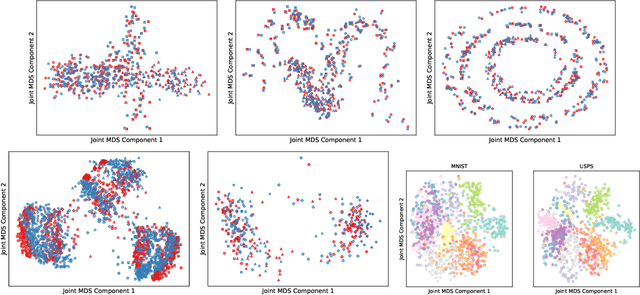

Abstract:We introduce Joint Multidimensional Scaling, a novel approach for unsupervised manifold alignment, which maps datasets from two different domains, without any known correspondences between data instances across the datasets, to a common low-dimensional Euclidean space. Our approach integrates Multidimensional Scaling (MDS) and Wasserstein Procrustes analysis into a joint optimization problem to simultaneously generate isometric embeddings of data and learn correspondences between instances from two different datasets, while only requiring intra-dataset pairwise dissimilarities as input. This unique characteristic makes our approach applicable to datasets without access to the input features, such as solving the inexact graph matching problem. We propose an alternating optimization scheme to solve the problem that can fully benefit from the optimization techniques for MDS and Wasserstein Procrustes. We demonstrate the effectiveness of our approach in several applications, including joint visualization of two datasets, unsupervised heterogeneous domain adaptation, graph matching, and protein structure alignment.
Approximate Network Motif Mining Via Graph Learning
Jun 07, 2022


Abstract:Frequent and structurally related subgraphs, also known as network motifs, are valuable features of many graph datasets. However, the high computational complexity of identifying motif sets in arbitrary datasets (motif mining) has limited their use in many real-world datasets. By automatically leveraging statistical properties of datasets, machine learning approaches have shown promise in several tasks with combinatorial complexity and are therefore a promising candidate for network motif mining. In this work we seek to facilitate the development of machine learning approaches aimed at motif mining. We propose a formulation of the motif mining problem as a node labelling task. In addition, we build benchmark datasets and evaluation metrics which test the ability of models to capture different aspects of motif discovery such as motif number, size, topology, and scarcity. Next, we propose MotiFiesta, a first attempt at solving this problem in a fully differentiable manner with promising results on challenging baselines. Finally, we demonstrate through MotiFiesta that this learning setting can be applied simultaneously to general-purpose data mining and interpretable feature extraction for graph classification tasks.
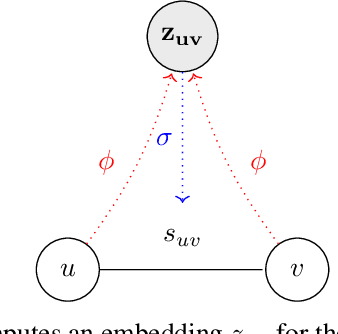
Structure-Aware Transformer for Graph Representation Learning
Feb 07, 2022
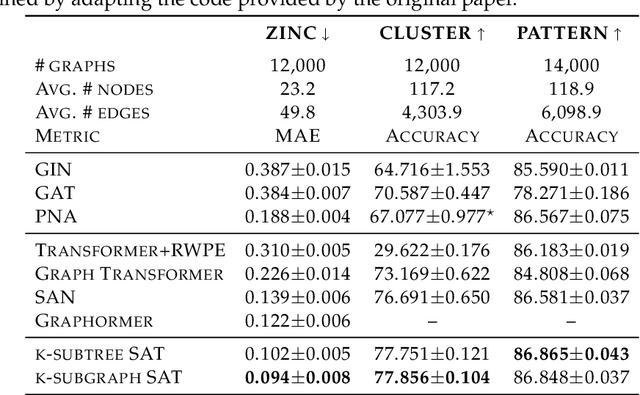
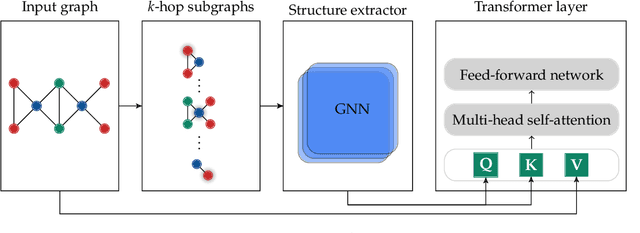
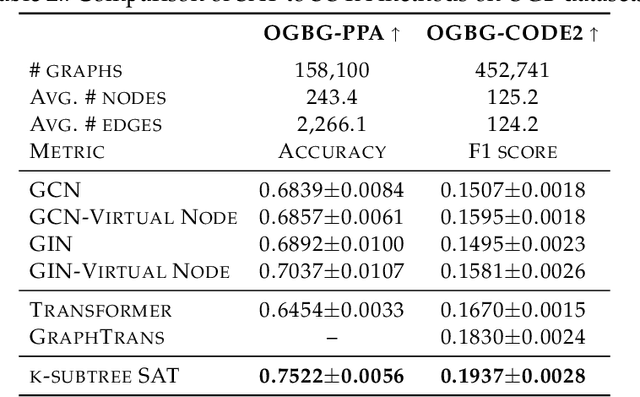
Abstract:The Transformer architecture has gained growing attention in graph representation learning recently, as it naturally overcomes several limitations of graph neural networks (GNNs) by avoiding their strict structural inductive biases and instead only encoding the graph structure via positional encoding. Here, we show that the node representations generated by the Transformer with positional encoding do not necessarily capture structural similarity between them. To address this issue, we propose the Structure-Aware Transformer, a class of simple and flexible graph transformers built upon a new self-attention mechanism. This new self-attention incorporates structural information into the original self-attention by extracting a subgraph representation rooted at each node before computing the attention. We propose several methods for automatically generating the subgraph representation and show theoretically that the resulting representations are at least as expressive as the subgraph representations. Empirically, our method achieves state-of-the-art performance on five graph prediction benchmarks. Our structure-aware framework can leverage any existing GNN to extract the subgraph representation, and we show that it systematically improves performance relative to the base GNN model, successfully combining the advantages of GNNs and transformers.
Weisfeiler and Leman go Machine Learning: The Story so far
Dec 18, 2021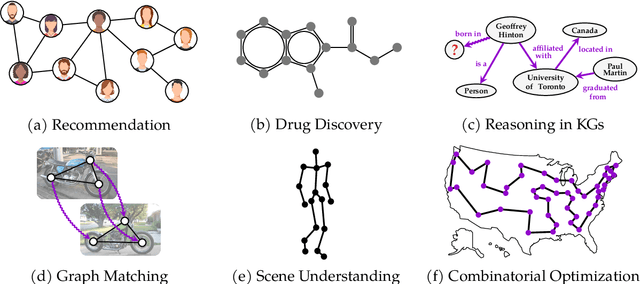
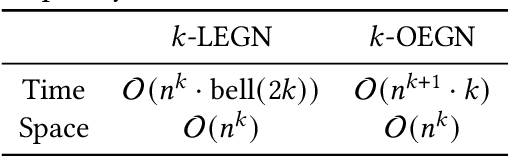
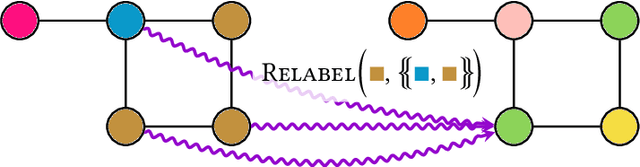

Abstract:In recent years, algorithms and neural architectures based on the Weisfeiler-Leman algorithm, a well-known heuristic for the graph isomorphism problem, emerged as a powerful tool for machine learning with graphs and relational data. Here, we give a comprehensive overview of the algorithm's use in a machine learning setting, focusing on the supervised regime. We discuss the theoretical background, show how to use it for supervised graph- and node representation learning, discuss recent extensions, and outline the algorithm's connection to (permutation-)equivariant neural architectures. Moreover, we give an overview of current applications and future directions to stimulate further research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge