Endowing Protein Language Models with Structural Knowledge

Understanding the relationships between protein sequence, structure and function is a long-standing biological challenge with manifold implications from drug design to our understanding of evolution. Recently, protein language models have emerged as the preferred method for this challenge, thanks to their ability to harness large sequence databases. Yet, their reliance on expansive sequence data and parameter sets limits their flexibility and practicality in real-world scenarios. Concurrently, the recent surge in computationally predicted protein structures unlocks new opportunities in protein representation learning. While promising, the computational burden carried by such complex data still hinders widely-adopted practical applications. To address these limitations, we introduce a novel framework that enhances protein language models by integrating protein structural data. Drawing from recent advances in graph transformers, our approach refines the self-attention mechanisms of pretrained language transformers by integrating structural information with structure extractor modules. This refined model, termed Protein Structure Transformer (PST), is further pretrained on a small protein structure database, using the same masked language modeling objective as traditional protein language models. Empirical evaluations of PST demonstrate its superior parameter efficiency relative to protein language models, despite being pretrained on a dataset comprising only 542K structures. Notably, PST consistently outperforms the state-of-the-art foundation model for protein sequences, ESM-2, setting a new benchmark in protein function prediction. Our findings underscore the potential of integrating structural information into protein language models, paving the way for more effective and efficient protein modeling Code and pretrained models are available at https://github.com/BorgwardtLab/PST.

Fisher Information Embedding for Node and Graph Learning

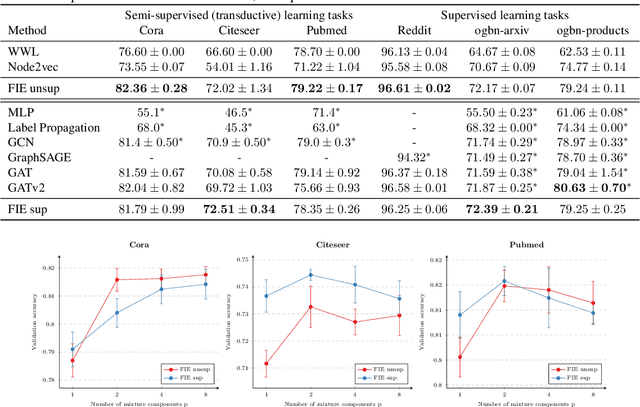
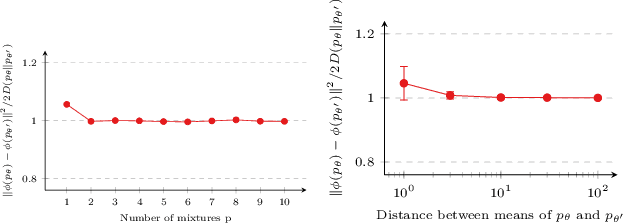
Attention-based graph neural networks (GNNs), such as graph attention networks (GATs), have become popular neural architectures for processing graph-structured data and learning node embeddings. Despite their empirical success, these models rely on labeled data and the theoretical properties of these models have yet to be fully understood. In this work, we propose a novel attention-based node embedding framework for graphs. Our framework builds upon a hierarchical kernel for multisets of subgraphs around nodes (e.g. neighborhoods) and each kernel leverages the geometry of a smooth statistical manifold to compare pairs of multisets, by "projecting" the multisets onto the manifold. By explicitly computing node embeddings with a manifold of Gaussian mixtures, our method leads to a new attention mechanism for neighborhood aggregation. We provide theoretical insights into genralizability and expressivity of our embeddings, contributing to a deeper understanding of attention-based GNNs. We propose efficient unsupervised and supervised methods for learning the embeddings, with the unsupervised method not requiring any labeled data. Through experiments on several node classification benchmarks, we demonstrate that our proposed method outperforms existing attention-based graph models like GATs. Our code is available at https://github.com/BorgwardtLab/fisher_information_embedding.

k-Center Clustering with Outliers in Sliding Windows

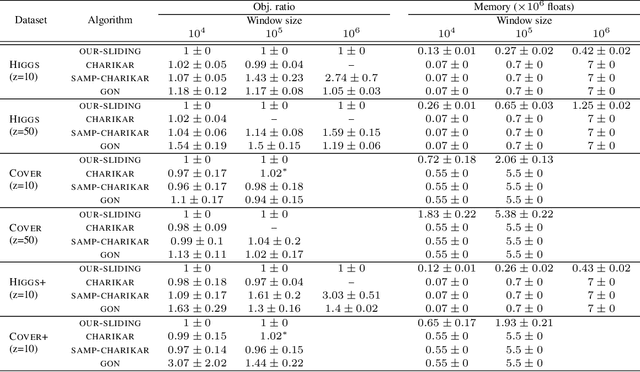
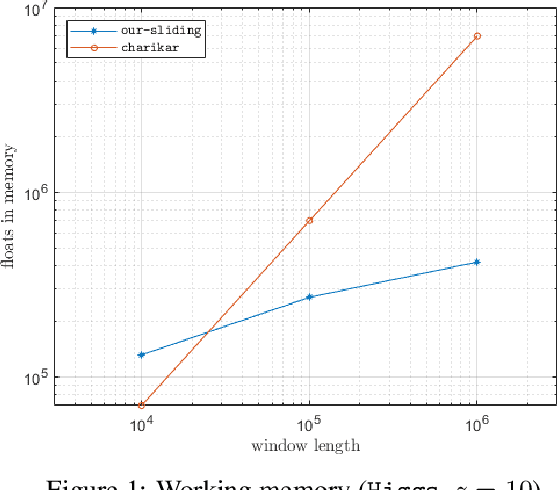
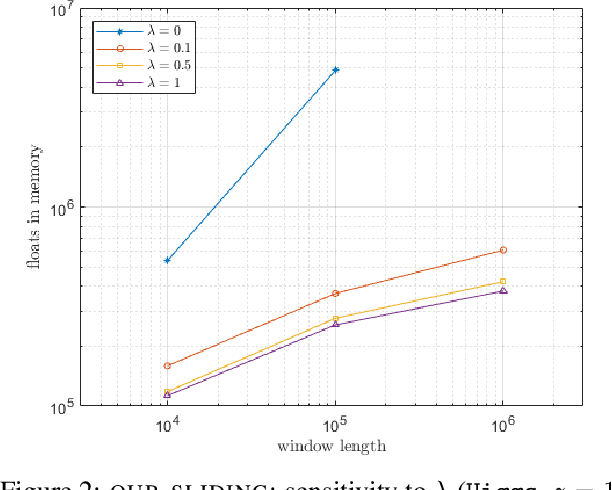
Metric $k$-center clustering is a fundamental unsupervised learning primitive. Although widely used, this primitive is heavily affected by noise in the data, so that a more sensible variant seeks for the best solution that disregards a given number $z$ of points of the dataset, called outliers. We provide efficient algorithms for this important variant in the streaming model under the sliding window setting, where, at each time step, the dataset to be clustered is the window $W$ of the most recent data items. Our algorithms achieve $O(1)$ approximation and, remarkably, require a working memory linear in $k+z$ and only logarithmic in $|W|$. As a by-product, we show how to estimate the effective diameter of the window $W$, which is a measure of the spread of the window points, disregarding a given fraction of noisy distances. We also provide experimental evidence of the practical viability of our theoretical results.