Scalable and Distributed Silhouette Approximation

The silhouette is one of the most widely used measures to assess the quality of a $k$-clustering of a dataset of $n$ elements. Its evaluation requires no information beyond the clustering assignment. In addition, the silhouette is extremely easy to interpret, providing a score to measure the quality of a clustering as a whole or for each element. The exact computation of the: (i) silhouette of each element of a dataset; and (ii) the global silhouette of the clustering; require $Θ(n^2)$ distance calculations, under general metrics. The quadratic complexity $Θ(n^2)$ is extremely prohibitive, especially on massive modern datasets. Surprisingly, existing approximate methods using $O(n^2)$ distance calculations are heuristics not offering provable and controllable guarantees on the quality of their results. We introduce the first rigorous and efficient algorithms to estimate: (i) the (local) silhouette of each element of a dataset; and (ii) the (global) silhouette; of any metric $k$-clustering. Our methods, based on sampling, perform $O(nk\varepsilon^{-2}\ln (nk/δ))$ distance computations, and provide estimates with additive error $O(\varepsilon)$ with probability at least $1-δ$. That is, parameters $\varepsilon$ and $δ$ in $(0,1)$ control the trade-off between accuracy and efficiency. We also introduce a scalable and distributed design of our methods for the MapReduce and Massively Parallel Computing (MPC) frameworks. Our distributed algorithms use a constant number of rounds and sublinear local memory. Finally, we perform extensive experiments against state-of-the-art approaches. The results show that our new techniques yield the best trade-off between accuracy and efficiency for both local and global silhouette estimation. In addition, our methods scale efficiently to massive datasets for which an exact computation of the silhouette is not practical.

Distributed k-Means with Outliers in General Metrics

Center-based clustering is a pivotal primitive for unsupervised learning and data analysis. A popular variant is undoubtedly the k-means problem, which, given a set $P$ of points from a metric space and a parameter $k<|P|$, requires to determine a subset $S$ of $k$ centers minimizing the sum of all squared distances of points in $P$ from their closest center. A more general formulation, known as k-means with $z$ outliers, introduced to deal with noisy datasets, features a further parameter $z$ and allows up to $z$ points of $P$ (outliers) to be disregarded when computing the aforementioned sum. We present a distributed coreset-based 3-round approximation algorithm for k-means with $z$ outliers for general metric spaces, using MapReduce as a computational model. Our distributed algorithm requires sublinear local memory per reducer, and yields a solution whose approximation ratio is an additive term $O(\gamma)$ away from the one achievable by the best known sequential (possibly bicriteria) algorithm, where $\gamma$ can be made arbitrarily small. An important feature of our algorithm is that it obliviously adapts to the intrinsic complexity of the dataset, captured by the doubling dimension $D$ of the metric space. To the best of our knowledge, no previous distributed approaches were able to attain similar quality-performance tradeoffs for general metrics.

k-Center Clustering with Outliers in Sliding Windows

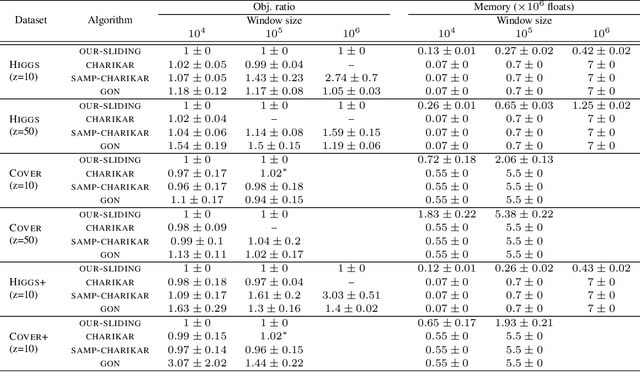
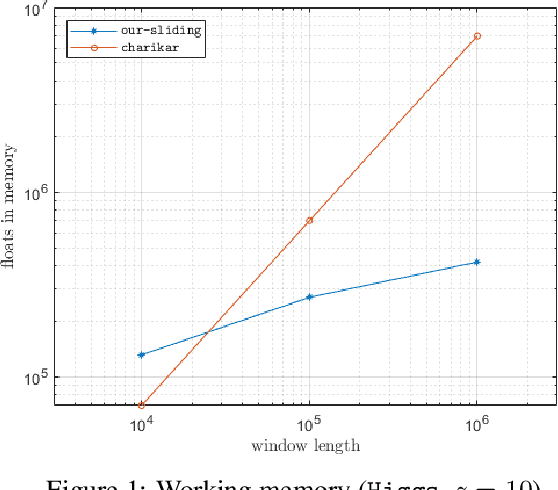
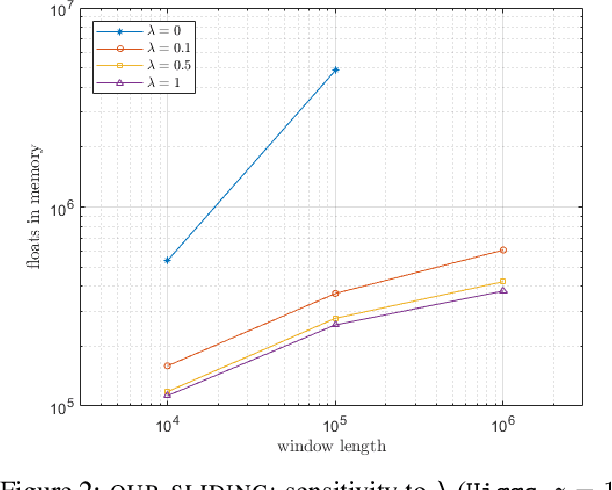
Metric $k$-center clustering is a fundamental unsupervised learning primitive. Although widely used, this primitive is heavily affected by noise in the data, so that a more sensible variant seeks for the best solution that disregards a given number $z$ of points of the dataset, called outliers. We provide efficient algorithms for this important variant in the streaming model under the sliding window setting, where, at each time step, the dataset to be clustered is the window $W$ of the most recent data items. Our algorithms achieve $O(1)$ approximation and, remarkably, require a working memory linear in $k+z$ and only logarithmic in $|W|$. As a by-product, we show how to estimate the effective diameter of the window $W$, which is a measure of the spread of the window points, disregarding a given fraction of noisy distances. We also provide experimental evidence of the practical viability of our theoretical results.

Scalable Distributed Approximation of Internal Measures for Clustering Evaluation

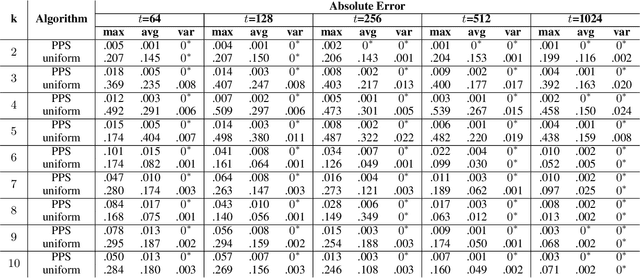
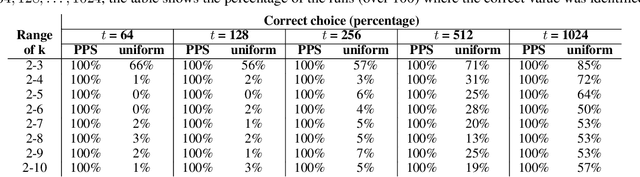
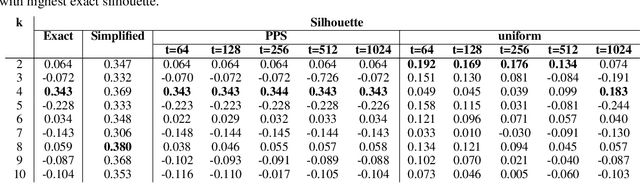
The most widely used internal measure for clustering evaluation is the silhouette coefficient, whose naive computation requires a quadratic number of distance calculations, which is clearly unfeasible for massive datasets. Surprisingly, there are no known general methods to efficiently approximate the silhouette coefficient of a clustering with rigorously provable high accuracy. In this paper, we present the first scalable algorithm to compute such a rigorous approximation for the evaluation of clusterings based on any metric distances. Our algorithm hinges on a Probability Proportional to Size (PPS) sampling scheme, and, for any fixed $\varepsilon, \delta \in (0,1)$, it approximates the silhouette coefficient within a mere additive error $O(\varepsilon)$ with probability $1-\delta$, using a very small number of distance calculations. We also prove that the algorithm can be adapted to obtain rigorous approximations of other internal measures of clustering quality, such as cohesion and separation. Importantly, we provide a distributed implementation of the algorithm using the MapReduce model, which runs in constant rounds and requires only sublinear local space at each worker, which makes our estimation approach applicable to big data scenarios. We perform an extensive experimental evaluation of our silhouette approximation algorithm, comparing its performance to a number of baseline heuristics on real and synthetic datasets. The experiments provide evidence that, unlike other heuristics, our estimation strategy not only provides tight theoretical guarantees but is also able to return highly accurate estimations while running in a fraction of the time required by the exact computation, and that its distributed implementation is highly scalable, thus enabling the computation of internal measures for very large datasets for which the exact computation is prohibitive.

Coreset-based Strategies for Robust Center-type Problems

Given a dataset $V$ of points from some metric space, the popular $k$-center problem requires to identify a subset of $k$ points (centers) in $V$ minimizing the maximum distance of any point of $V$ from its closest center. The \emph{robust} formulation of the problem features a further parameter $z$ and allows up to $z$ points of $V$ (outliers) to be disregarded when computing the maximum distance from the centers. In this paper, we focus on two important constrained variants of the robust $k$-center problem, namely, the Robust Matroid Center (RMC) problem, where the set of returned centers are constrained to be an independent set of a matroid of rank $k$ built on $V$, and the Robust Knapsack Center (RKC) problem, where each element $i\in V$ is given a positive weight $w_i<1$ and the aggregate weight of the returned centers must be at most 1. We devise coreset-based strategies for the two problems which yield efficient sequential, MapReduce, and Streaming algorithms. More specifically, for any fixed $\epsilon>0$, the algorithms return solutions featuring a $(3+\epsilon)$-approximation ratio, which is a mere additive term $\epsilon$ away from the 3-approximations achievable by the best known polynomial-time sequential algorithms for the two problems. Moreover, the algorithms obliviously adapt to the intrinsic complexity of the dataset, captured by its doubling dimension $D$. For wide ranges of the parameters $k,z,\epsilon, D$, we obtain a sequential algorithm with running time linear in $|V|$, and MapReduce/Streaming algorithms with few rounds/passes and substantially sublinear local/working memory.