Unsupervised Manifold Alignment with Joint Multidimensional Scaling
Paper and Code
Jul 06, 2022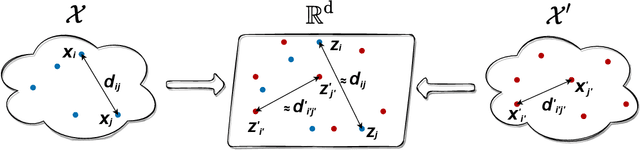
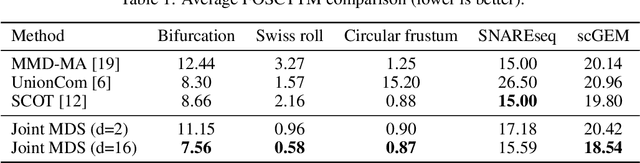
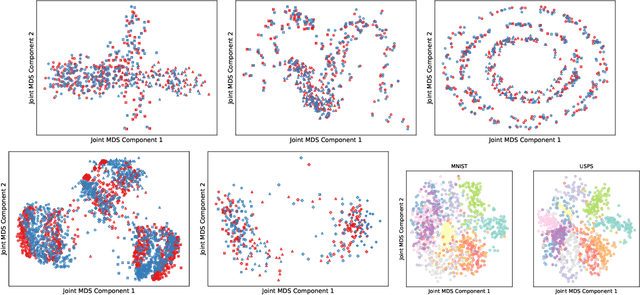

We introduce Joint Multidimensional Scaling, a novel approach for unsupervised manifold alignment, which maps datasets from two different domains, without any known correspondences between data instances across the datasets, to a common low-dimensional Euclidean space. Our approach integrates Multidimensional Scaling (MDS) and Wasserstein Procrustes analysis into a joint optimization problem to simultaneously generate isometric embeddings of data and learn correspondences between instances from two different datasets, while only requiring intra-dataset pairwise dissimilarities as input. This unique characteristic makes our approach applicable to datasets without access to the input features, such as solving the inexact graph matching problem. We propose an alternating optimization scheme to solve the problem that can fully benefit from the optimization techniques for MDS and Wasserstein Procrustes. We demonstrate the effectiveness of our approach in several applications, including joint visualization of two datasets, unsupervised heterogeneous domain adaptation, graph matching, and protein structure alignment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge