A Generalized Weisfeiler-Lehman Graph Kernel
Paper and Code
Jan 20, 2021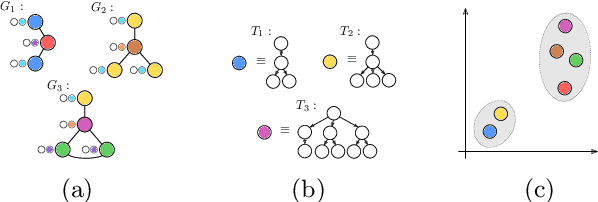
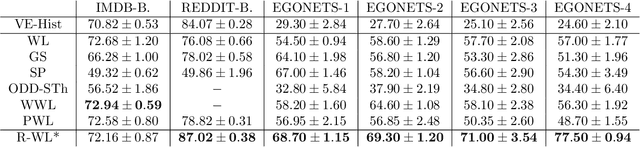
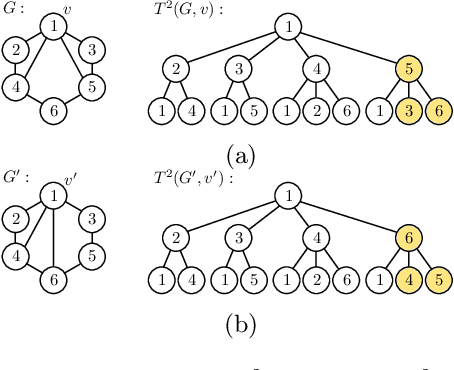
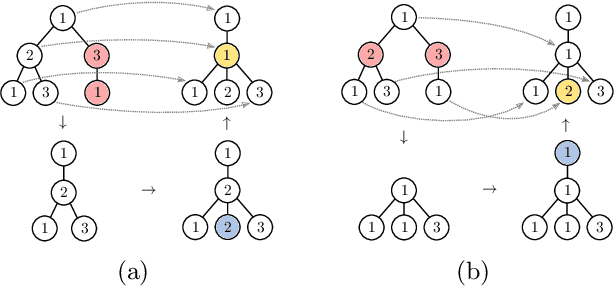
The Weisfeiler-Lehman graph kernels are among the most prevalent graph kernels due to their remarkable time complexity and predictive performance. Their key concept is based on an implicit comparison of neighborhood representing trees with respect to equality (i.e., isomorphism). This binary valued comparison is, however, arguably too rigid for defining suitable similarity measures over graphs. To overcome this limitation, we propose a generalization of Weisfeiler-Lehman graph kernels which takes into account the similarity between trees rather than equality. We achieve this using a specifically fitted variation of the well-known tree edit distance which can efficiently be calculated. We empirically show that our approach significantly outperforms state-of-the-art methods in terms of predictive performance on datasets containing structurally more complex graphs beyond the typically considered molecular graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge