A Survey on Uncertainty Toolkits for Deep Learning

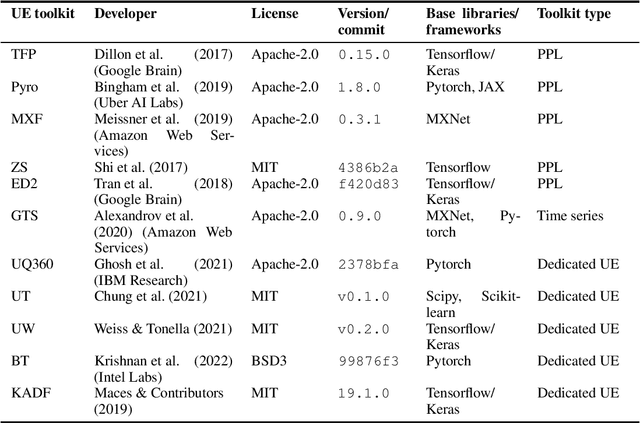
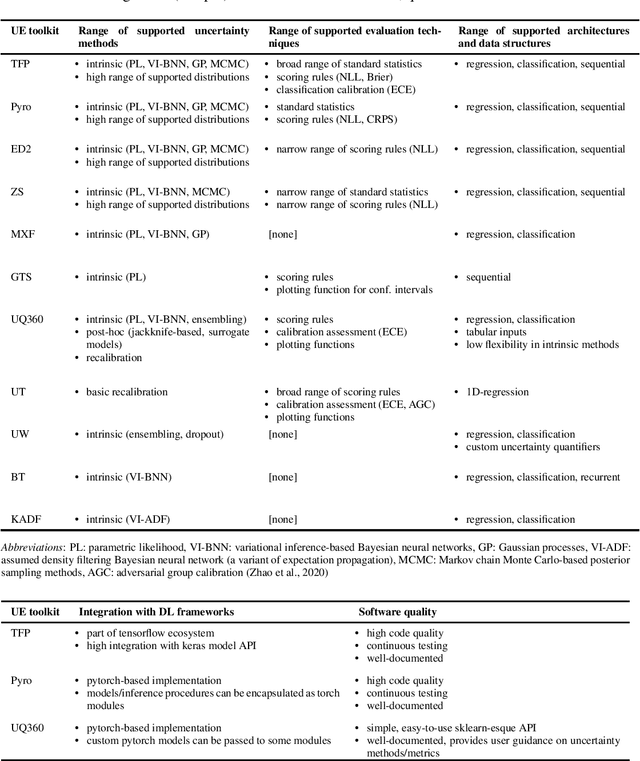
The success of deep learning (DL) fostered the creation of unifying frameworks such as tensorflow or pytorch as much as it was driven by their creation in return. Having common building blocks facilitates the exchange of, e.g., models or concepts and makes developments easier replicable. Nonetheless, robust and reliable evaluation and assessment of DL models has often proven challenging. This is at odds with their increasing safety relevance, which recently culminated in the field of "trustworthy ML". We believe that, among others, further unification of evaluation and safeguarding methodologies in terms of toolkits, i.e., small and specialized framework derivatives, might positively impact problems of trustworthiness as well as reproducibility. To this end, we present the first survey on toolkits for uncertainty estimation (UE) in DL, as UE forms a cornerstone in assessing model reliability. We investigate 11 toolkits with respect to modeling and evaluation capabilities, providing an in-depth comparison for the three most promising ones, namely Pyro, Tensorflow Probability, and Uncertainty Quantification 360. While the first two provide a large degree of flexibility and seamless integration into their respective framework, the last one has the larger methodological scope.

A Novel Regression Loss for Non-Parametric Uncertainty Optimization

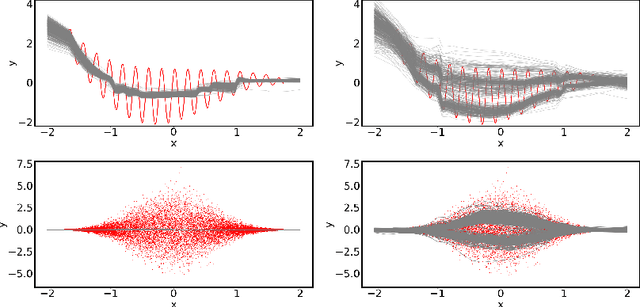
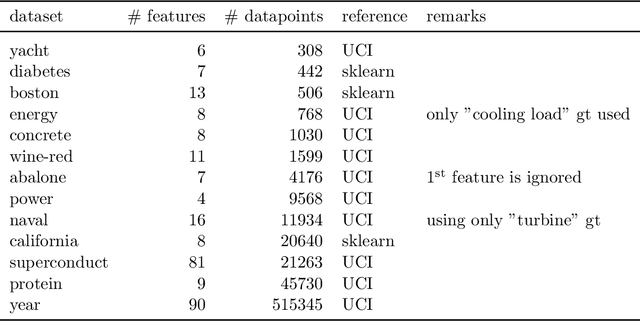
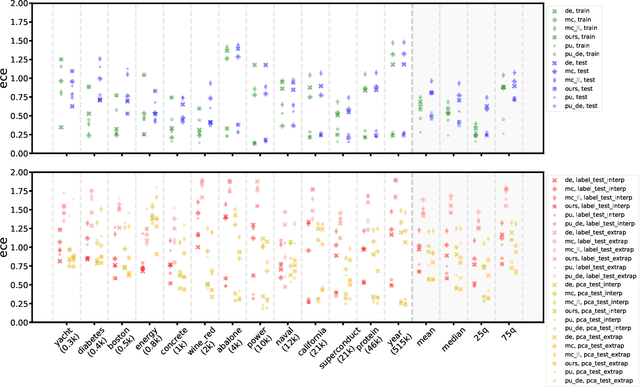
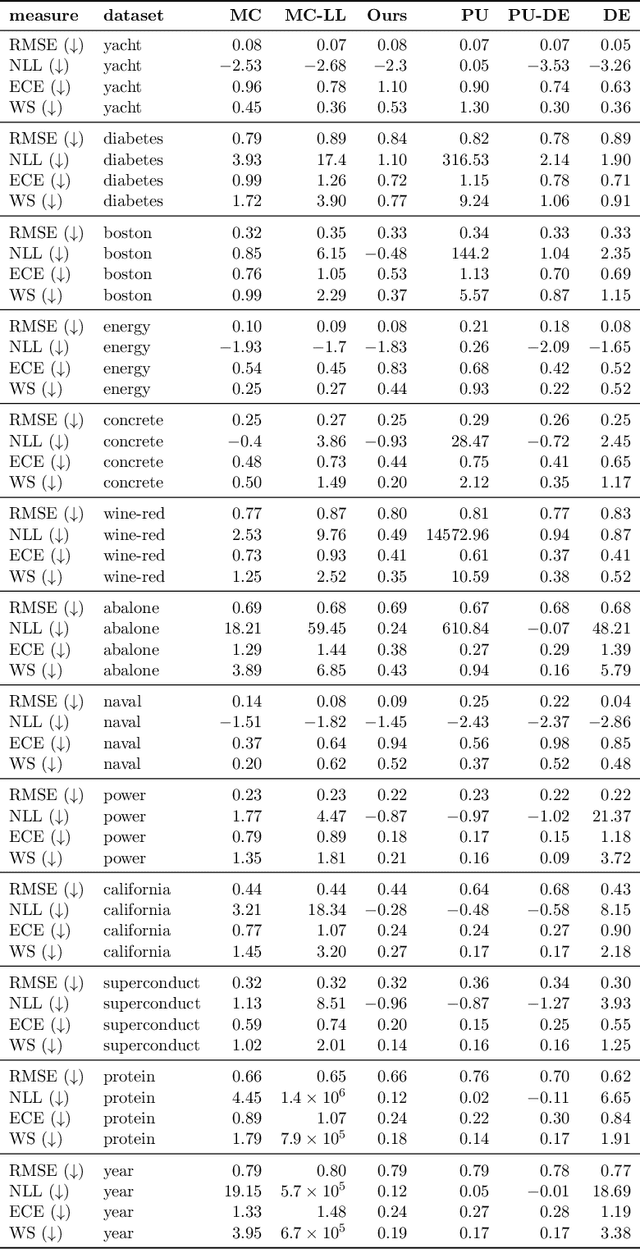
Quantification of uncertainty is one of the most promising approaches to establish safe machine learning. Despite its importance, it is far from being generally solved, especially for neural networks. One of the most commonly used approaches so far is Monte Carlo dropout, which is computationally cheap and easy to apply in practice. However, it can underestimate the uncertainty. We propose a new objective, referred to as second-moment loss (SML), to address this issue. While the full network is encouraged to model the mean, the dropout networks are explicitly used to optimize the model variance. We intensively study the performance of the new objective on various UCI regression datasets. Comparing to the state-of-the-art of deep ensembles, SML leads to comparable prediction accuracies and uncertainty estimates while only requiring a single model. Under distribution shift, we observe moderate improvements. As a side result, we introduce an intuitive Wasserstein distance-based uncertainty measure that is non-saturating and thus allows to resolve quality differences between any two uncertainty estimates.

Second-Moment Loss: A Novel Regression Objective for Improved Uncertainties

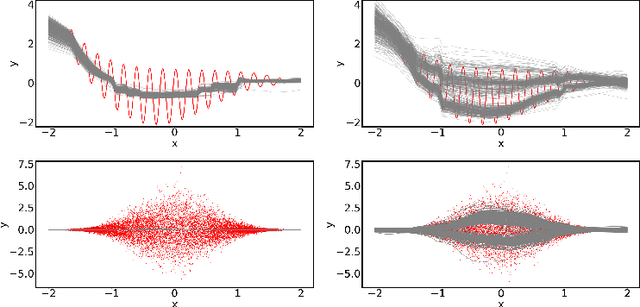
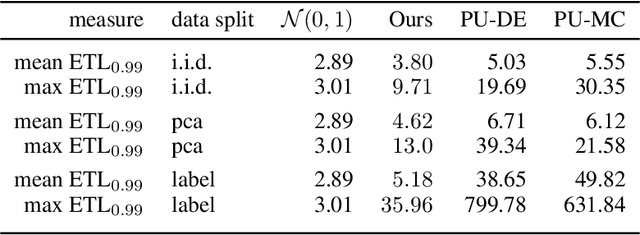
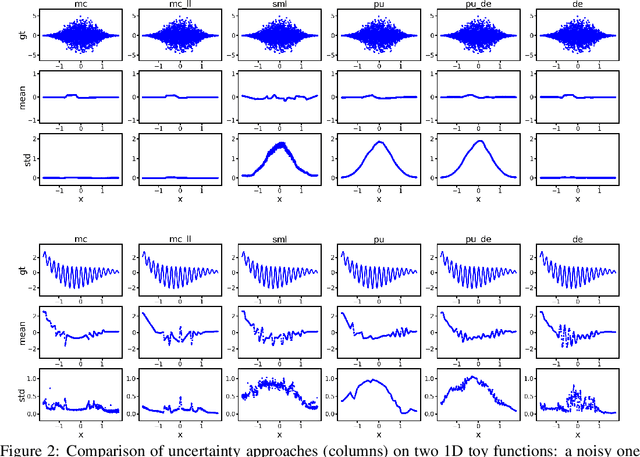
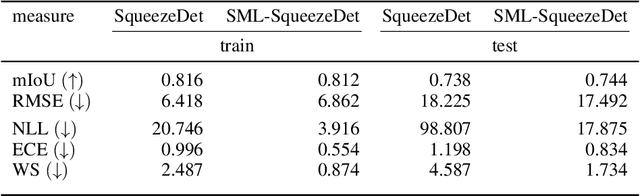
Quantification of uncertainty is one of the most promising approaches to establish safe machine learning. Despite its importance, it is far from being generally solved, especially for neural networks. One of the most commonly used approaches so far is Monte Carlo dropout, which is computationally cheap and easy to apply in practice. However, it can underestimate the uncertainty. We propose a new objective, referred to as second-moment loss (SML), to address this issue. While the full network is encouraged to model the mean, the dropout networks are explicitly used to optimize the model variance. We analyze the performance of the new objective on various toy and UCI regression datasets. Comparing to the state-of-the-art of deep ensembles, SML leads to comparable prediction accuracies and uncertainty estimates while only requiring a single model. Under distribution shift, we observe moderate improvements. From a safety perspective also the study of worst-case uncertainties is crucial. In this regard we improve considerably. Finally, we show that SML can be successfully applied to SqueezeDet, a modern object detection network. We improve on its uncertainty-related scores while not deteriorating regression quality. As a side result, we introduce an intuitive Wasserstein distance-based uncertainty measure that is non-saturating and thus allows to resolve quality differences between any two uncertainty estimates.

DenseHMM: Learning Hidden Markov Models by Learning Dense Representations

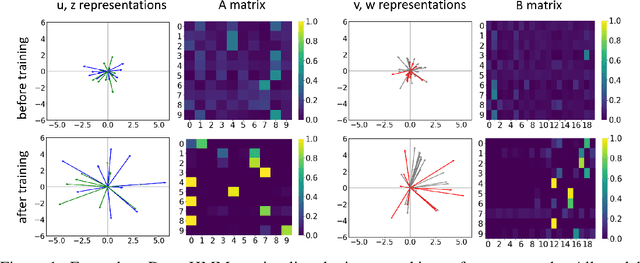
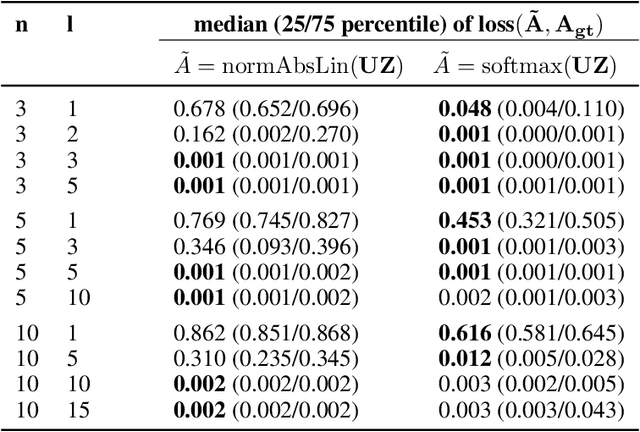
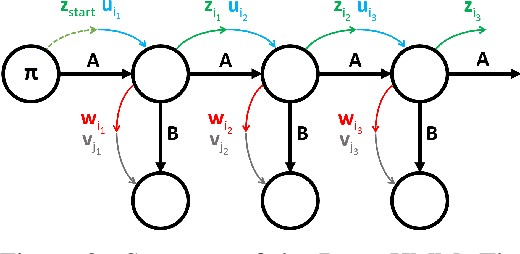
We propose DenseHMM - a modification of Hidden Markov Models (HMMs) that allows to learn dense representations of both the hidden states and the observables. Compared to the standard HMM, transition probabilities are not atomic but composed of these representations via kernelization. Our approach enables constraint-free and gradient-based optimization. We propose two optimization schemes that make use of this: a modification of the Baum-Welch algorithm and a direct co-occurrence optimization. The latter one is highly scalable and comes empirically without loss of performance compared to standard HMMs. We show that the non-linearity of the kernelization is crucial for the expressiveness of the representations. The properties of the DenseHMM like learned co-occurrences and log-likelihoods are studied empirically on synthetic and biomedical datasets.