DenseHMM: Learning Hidden Markov Models by Learning Dense Representations
Paper and Code
Dec 17, 2020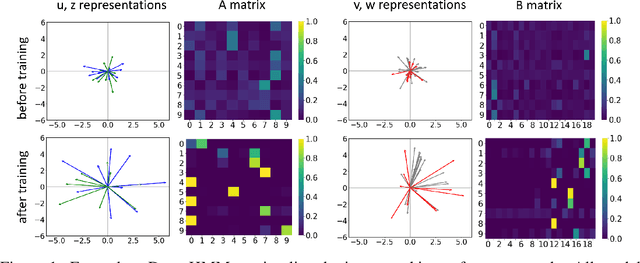
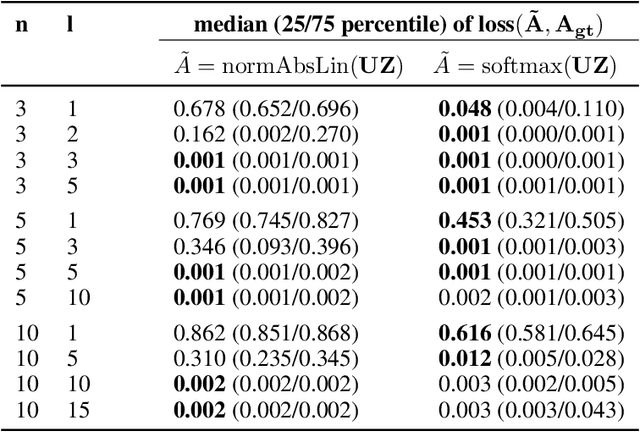
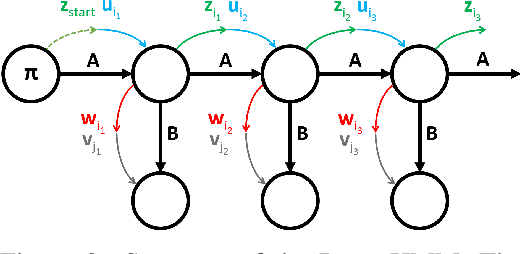
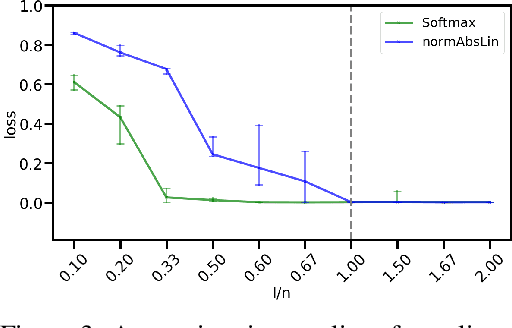
We propose DenseHMM - a modification of Hidden Markov Models (HMMs) that allows to learn dense representations of both the hidden states and the observables. Compared to the standard HMM, transition probabilities are not atomic but composed of these representations via kernelization. Our approach enables constraint-free and gradient-based optimization. We propose two optimization schemes that make use of this: a modification of the Baum-Welch algorithm and a direct co-occurrence optimization. The latter one is highly scalable and comes empirically without loss of performance compared to standard HMMs. We show that the non-linearity of the kernelization is crucial for the expressiveness of the representations. The properties of the DenseHMM like learned co-occurrences and log-likelihoods are studied empirically on synthetic and biomedical datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge