DFCon: Attention-Driven Supervised Contrastive Learning for Robust Deepfake Detection

This report presents our approach for the IEEE SP Cup 2025: Deepfake Face Detection in the Wild (DFWild-Cup), focusing on detecting deepfakes across diverse datasets. Our methodology employs advanced backbone models, including MaxViT, CoAtNet, and EVA-02, fine-tuned using supervised contrastive loss to enhance feature separation. These models were specifically chosen for their complementary strengths. Integration of convolution layers and strided attention in MaxViT is well-suited for detecting local features. In contrast, hybrid use of convolution and attention mechanisms in CoAtNet effectively captures multi-scale features. Robust pretraining with masked image modeling of EVA-02 excels at capturing global features. After training, we freeze the parameters of these models and train the classification heads. Finally, a majority voting ensemble is employed to combine the predictions from these models, improving robustness and generalization to unseen scenarios. The proposed system addresses the challenges of detecting deepfakes in real-world conditions and achieves a commendable accuracy of 95.83% on the validation dataset.

360Brew: A Decoder-only Foundation Model for Personalized Ranking and Recommendation

Ranking and recommendation systems are the foundation for numerous online experiences, ranging from search results to personalized content delivery. These systems have evolved into complex, multilayered architectures that leverage vast datasets and often incorporate thousands of predictive models. The maintenance and enhancement of these models is a labor intensive process that requires extensive feature engineering. This approach not only exacerbates technical debt but also hampers innovation in extending these systems to emerging problem domains. In this report, we present our research to address these challenges by utilizing a large foundation model with a textual interface for ranking and recommendation tasks. We illustrate several key advantages of our approach: (1) a single model can manage multiple predictive tasks involved in ranking and recommendation, (2) decoder models with textual interface due to their comprehension of reasoning capabilities, can generalize to new recommendation surfaces and out-of-domain problems, and (3) by employing natural language interfaces for task definitions and verbalizing member behaviors and their social connections, we eliminate the need for feature engineering and the maintenance of complex directed acyclic graphs of model dependencies. We introduce our research pre-production model, 360Brew V1.0, a 150B parameter, decoder-only model that has been trained and fine-tuned on LinkedIn's data and tasks. This model is capable of solving over 30 predictive tasks across various segments of the LinkedIn platform, achieving performance levels comparable to or exceeding those of current production systems based on offline metrics, without task-specific fine-tuning. Notably, each of these tasks is conventionally addressed by dedicated models that have been developed and maintained over multiple years by teams of a similar or larger size than our own.

LiGNN: Graph Neural Networks at LinkedIn

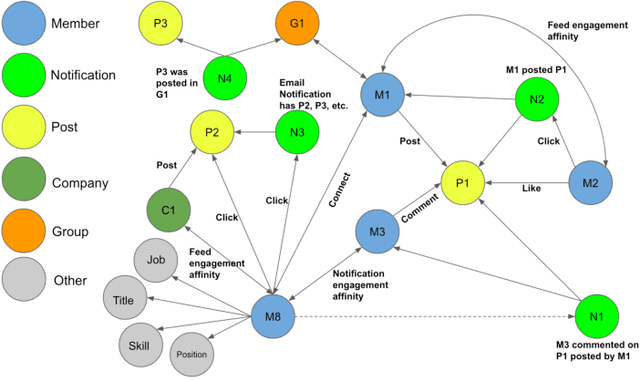
In this paper, we present LiGNN, a deployed large-scale Graph Neural Networks (GNNs) Framework. We share our insight on developing and deployment of GNNs at large scale at LinkedIn. We present a set of algorithmic improvements to the quality of GNN representation learning including temporal graph architectures with long term losses, effective cold start solutions via graph densification, ID embeddings and multi-hop neighbor sampling. We explain how we built and sped up by 7x our large-scale training on LinkedIn graphs with adaptive sampling of neighbors, grouping and slicing of training data batches, specialized shared-memory queue and local gradient optimization. We summarize our deployment lessons and learnings gathered from A/B test experiments. The techniques presented in this work have contributed to an approximate relative improvements of 1% of Job application hearing back rate, 2% Ads CTR lift, 0.5% of Feed engaged daily active users, 0.2% session lift and 0.1% weekly active user lift from people recommendation. We believe that this work can provide practical solutions and insights for engineers who are interested in applying Graph neural networks at large scale.

LiRank: Industrial Large Scale Ranking Models at LinkedIn

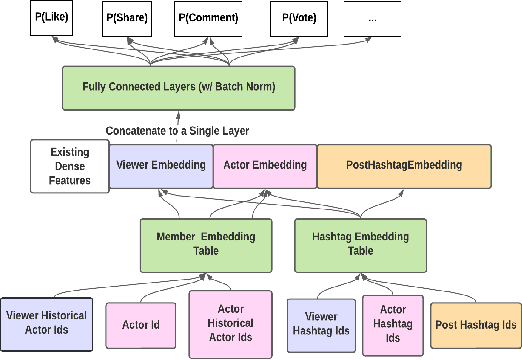
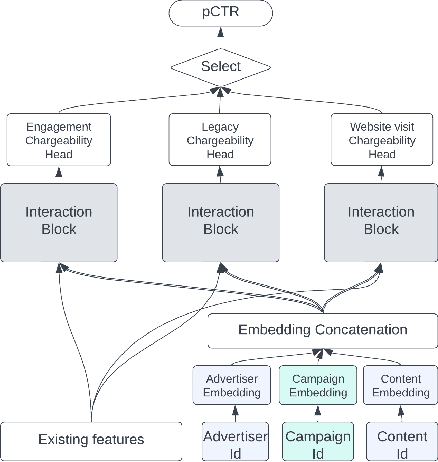
We present LiRank, a large-scale ranking framework at LinkedIn that brings to production state-of-the-art modeling architectures and optimization methods. We unveil several modeling improvements, including Residual DCN, which adds attention and residual connections to the famous DCNv2 architecture. We share insights into combining and tuning SOTA architectures to create a unified model, including Dense Gating, Transformers and Residual DCN. We also propose novel techniques for calibration and describe how we productionalized deep learning based explore/exploit methods. To enable effective, production-grade serving of large ranking models, we detail how to train and compress models using quantization and vocabulary compression. We provide details about the deployment setup for large-scale use cases of Feed ranking, Jobs Recommendations, and Ads click-through rate (CTR) prediction. We summarize our learnings from various A/B tests by elucidating the most effective technical approaches. These ideas have contributed to relative metrics improvements across the board at LinkedIn: +0.5% member sessions in the Feed, +1.76% qualified job applications for Jobs search and recommendations, and +4.3% for Ads CTR. We hope this work can provide practical insights and solutions for practitioners interested in leveraging large-scale deep ranking systems.

Measuring Long-term Impact of Ads on LinkedIn Feed

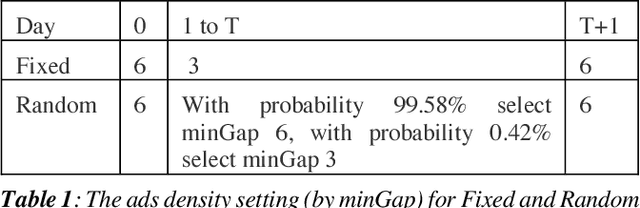
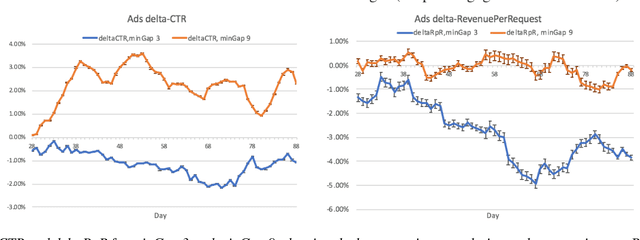
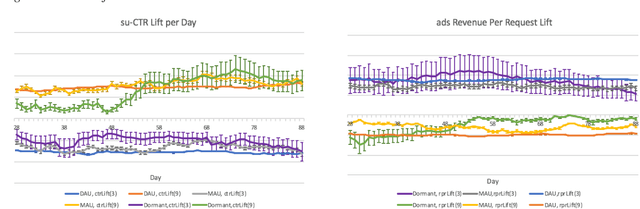
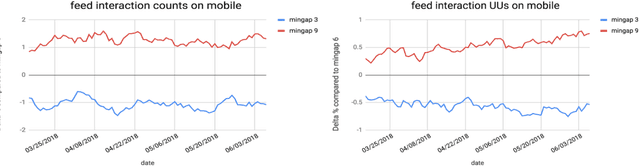
Organic updates (from a member's network) and sponsored updates (or ads, from advertisers) together form the newsfeed on LinkedIn. The newsfeed, the default homepage for members, attracts them to engage, brings them value and helps LinkedIn grow. Engagement and Revenue on feed are two critical, yet often conflicting objectives. Hence, it is important to design a good Revenue-Engagement Tradeoff (RENT) mechanism to blend ads in the feed. In this paper, we design experiments to understand how members' behavior evolve over time given different ads experiences. These experiences vary on ads density, while the quality of ads (ensured by relevance models) is held constant. Our experiments have been conducted on randomized member buckets and we use two experimental designs to measure the short term and long term effects of the various treatments. Based on the first three months' data, we observe that the long term impact is at a much smaller scale than the short term impact in our application. Furthermore, we observe different member cohorts (based on user activity level) adapt and react differently over time.

Analysis of Thompson Sampling for Gaussian Process Optimization in the Bandit Setting

We consider the global optimization of a function over a continuous domain. At every evaluation attempt, we can observe the function at a chosen point in the domain and we reap the reward of the value observed. We assume that drawing these observations are expensive and noisy. We frame it as a continuum-armed bandit problem with a Gaussian Process prior on the function. In this regime, most algorithms have been developed to minimize some form of regret. Contrary to this popular norm, in this paper, we study the convergence of the sequential point $\boldsymbol{x}^t$ to the global optimizer $\boldsymbol{x}^*$ for the Thompson Sampling approach. Under some assumptions and regularity conditions, we show an exponential rate of convergence to the true optimal.