Materials Learning Algorithms (MALA): Scalable Machine Learning for Electronic Structure Calculations in Large-Scale Atomistic Simulations

We present the Materials Learning Algorithms (MALA) package, a scalable machine learning framework designed to accelerate density functional theory (DFT) calculations suitable for large-scale atomistic simulations. Using local descriptors of the atomic environment, MALA models efficiently predict key electronic observables, including local density of states, electronic density, density of states, and total energy. The package integrates data sampling, model training and scalable inference into a unified library, while ensuring compatibility with standard DFT and molecular dynamics codes. We demonstrate MALA's capabilities with examples including boron clusters, aluminum across its solid-liquid phase boundary, and predicting the electronic structure of a stacking fault in a large beryllium slab. Scaling analyses reveal MALA's computational efficiency and identify bottlenecks for future optimization. With its ability to model electronic structures at scales far beyond standard DFT, MALA is well suited for modeling complex material systems, making it a versatile tool for advanced materials research.

Union: A Unified HW-SW Co-Design Ecosystem in MLIR for Evaluating Tensor Operations on Spatial Accelerators

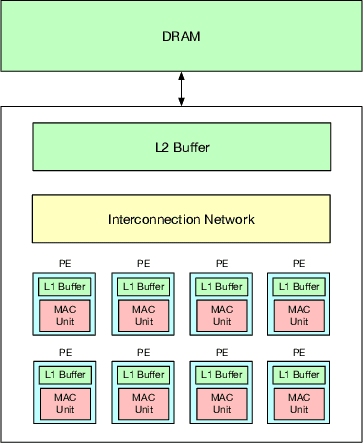
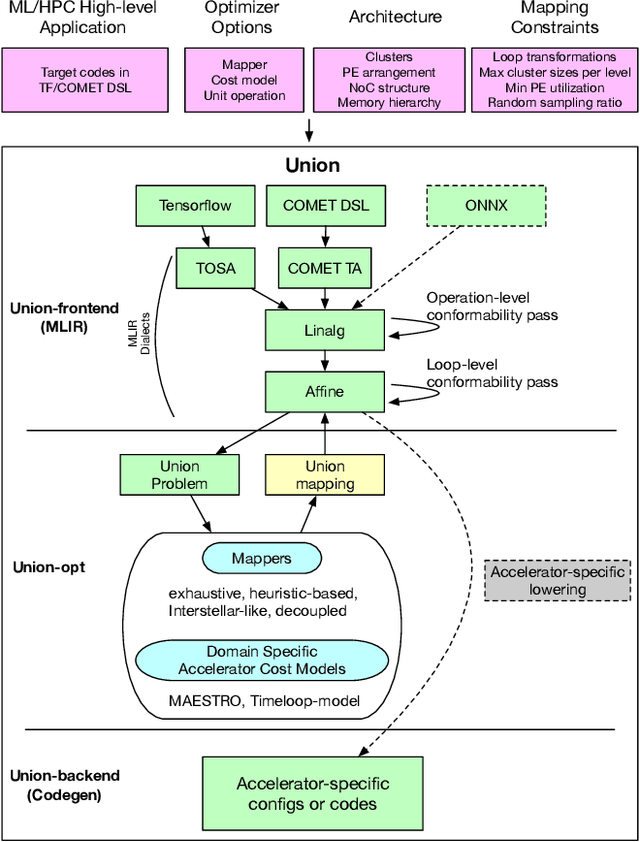
To meet the extreme compute demands for deep learning across commercial and scientific applications, dataflow accelerators are becoming increasingly popular. While these "domain-specific" accelerators are not fully programmable like CPUs and GPUs, they retain varying levels of flexibility with respect to data orchestration, i.e., dataflow and tiling optimizations to enhance efficiency. There are several challenges when designing new algorithms and mapping approaches to execute the algorithms for a target problem on new hardware. Previous works have addressed these challenges individually. To address this challenge as a whole, in this work, we present a HW-SW co-design ecosystem for spatial accelerators called Union within the popular MLIR compiler infrastructure. Our framework allows exploring different algorithms and their mappings on several accelerator cost models. Union also includes a plug-and-play library of accelerator cost models and mappers which can easily be extended. The algorithms and accelerator cost models are connected via a novel mapping abstraction that captures the map space of spatial accelerators which can be systematically pruned based on constraints from the hardware, workload, and mapper. We demonstrate the value of Union for the community with several case studies which examine offloading different tensor operations(CONV/GEMM/Tensor Contraction) on diverse accelerator architectures using different mapping schemes.

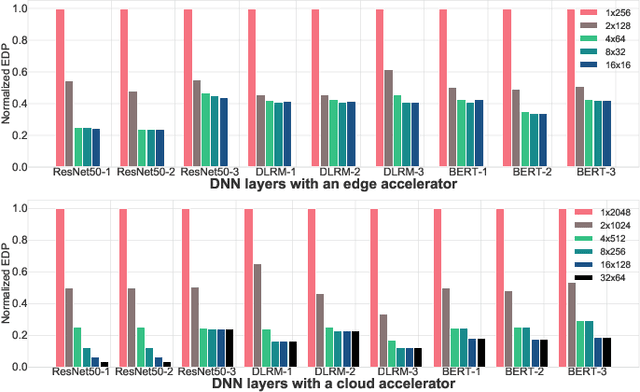
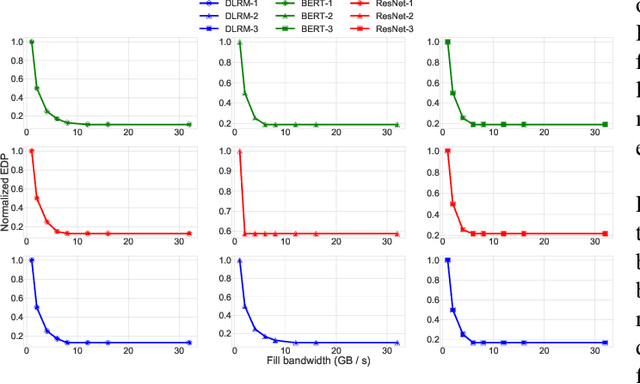
Evaluating Spatial Accelerator Architectures with Tiled Matrix-Matrix Multiplication

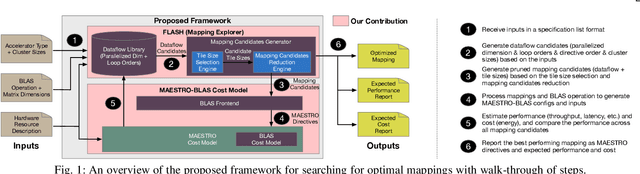
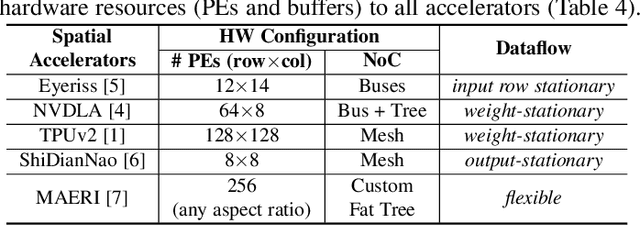
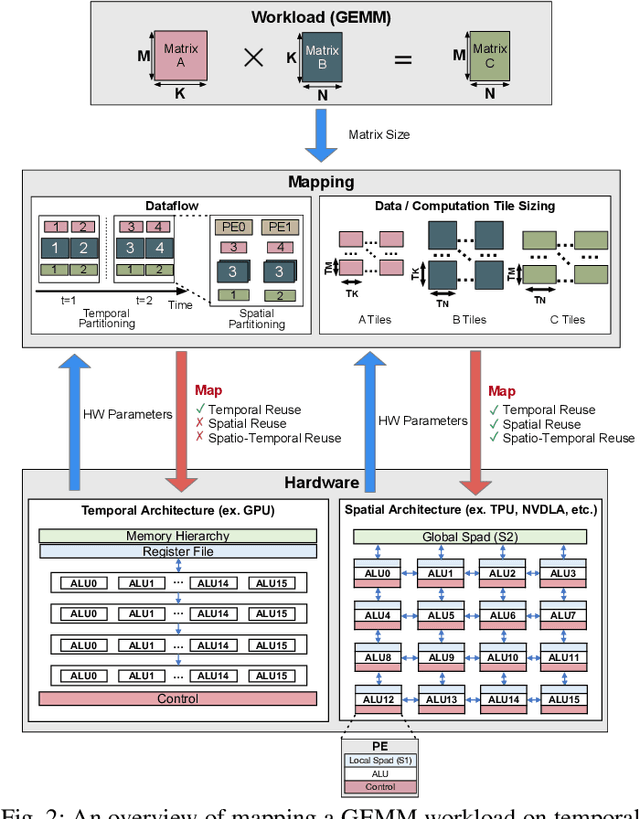
There is a growing interest in custom spatial accelerators for machine learning applications. These accelerators employ a spatial array of processing elements (PEs) interacting via custom buffer hierarchies and networks-on-chip. The efficiency of these accelerators comes from employing optimized dataflow (i.e., spatial/temporal partitioning of data across the PEs and fine-grained scheduling) strategies to optimize data reuse. The focus of this work is to evaluate these accelerator architectures using a tiled general matrix-matrix multiplication (GEMM) kernel. To do so, we develop a framework that finds optimized mappings (dataflow and tile sizes) for a tiled GEMM for a given spatial accelerator and workload combination, leveraging an analytical cost model for runtime and energy. Our evaluations over five spatial accelerators demonstrate that the tiled GEMM mappings systematically generated by our framework achieve high performance on various GEMM workloads and accelerators.

Concentric Spherical GNN for 3D Representation Learning

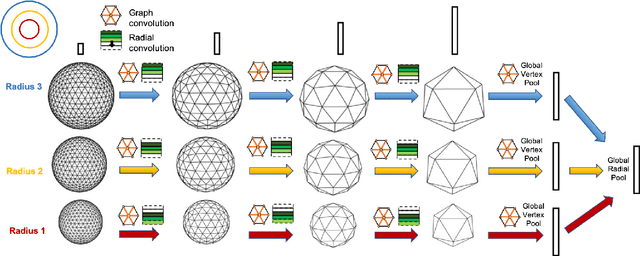
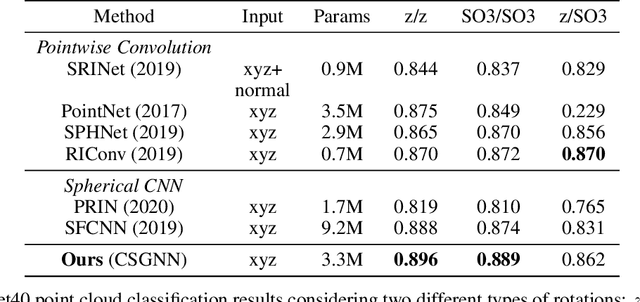
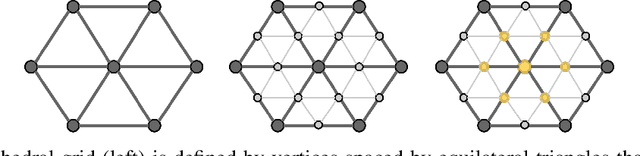
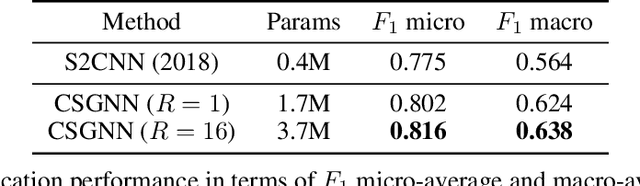
Learning 3D representations that generalize well to arbitrarily oriented inputs is a challenge of practical importance in applications varying from computer vision to physics and chemistry. We propose a novel multi-resolution convolutional architecture for learning over concentric spherical feature maps, of which the single sphere representation is a special case. Our hierarchical architecture is based on alternatively learning to incorporate both intra-sphere and inter-sphere information. We show the applicability of our method for two different types of 3D inputs, mesh objects, which can be regularly sampled, and point clouds, which are irregularly distributed. We also propose an efficient mapping of point clouds to concentric spherical images, thereby bridging spherical convolutions on grids with general point clouds. We demonstrate the effectiveness of our approach in improving state-of-the-art performance on 3D classification tasks with rotated data.

Accelerating Finite-temperature Kohn-Sham Density Functional Theory with Deep Neural Networks

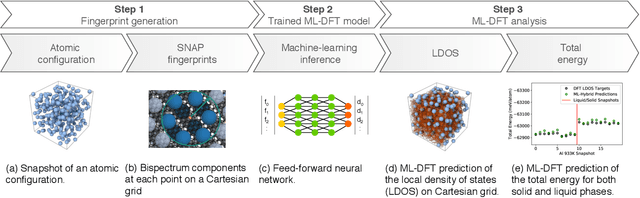
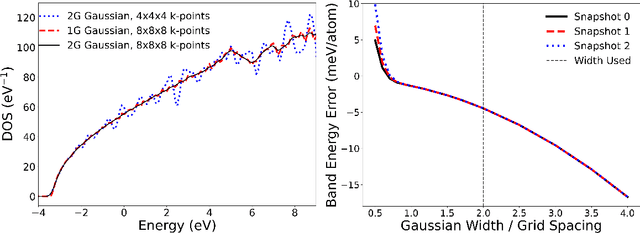
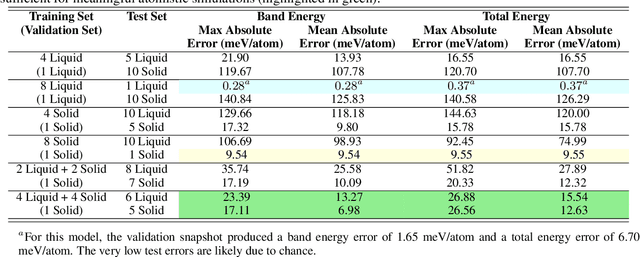
We present a numerical modeling workflow based on machine learning (ML) which reproduces the the total energies produced by Kohn-Sham density functional theory (DFT) at finite electronic temperature to within chemical accuracy at negligible computational cost. Based on deep neural networks, our workflow yields the local density of states (LDOS) for a given atomic configuration. From the LDOS, spatially-resolved, energy-resolved, and integrated quantities can be calculated, including the DFT total free energy, which serves as the Born-Oppenheimer potential energy surface for the atoms. We demonstrate the efficacy of this approach for both solid and liquid metals and compare results between independent and unified machine-learning models for solid and liquid aluminum. Our machine-learning density functional theory framework opens up the path towards multiscale materials modeling for matter under ambient and extreme conditions at a computational scale and cost that is unattainable with current algorithms.

How Robust Are Graph Neural Networks to Structural Noise?

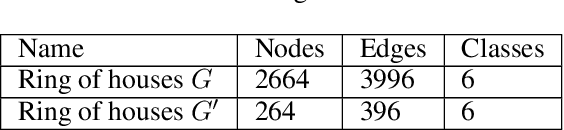
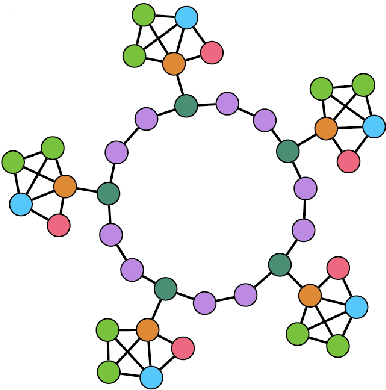
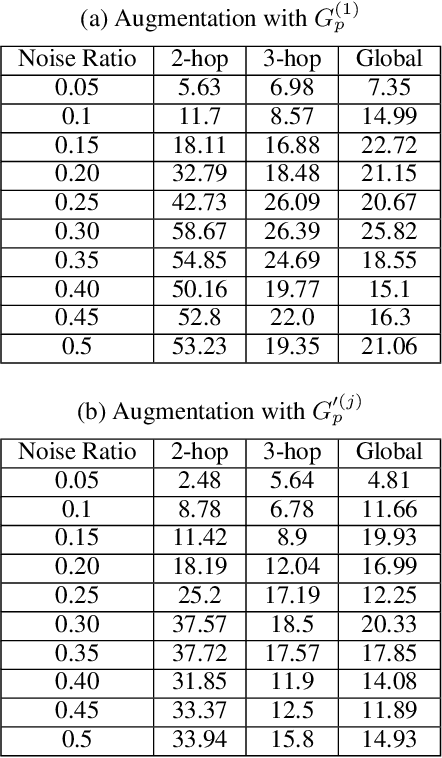
Graph neural networks (GNNs) are an emerging model for learning graph embeddings and making predictions on graph structured data. However, robustness of graph neural networks is not yet well-understood. In this work, we focus on node structural identity predictions, where a representative GNN model is able to achieve near-perfect accuracy. We also show that the same GNN model is not robust to addition of structural noise, through a controlled dataset and set of experiments. Finally, we show that under the right conditions, graph-augmented training is capable of significantly improving robustness to structural noise.