SDQ: Sparse Decomposed Quantization for LLM Inference

Recently, large language models (LLMs) have shown surprising performance in task-specific workloads as well as general tasks with the given prompts. However, to achieve unprecedented performance, recent LLMs use billions to trillions of parameters, which hinder the wide adaptation of those models due to their extremely large compute and memory requirements. To resolve the issue, various model compression methods are being actively investigated. In this work, we propose SDQ (Sparse Decomposed Quantization) to exploit both structured sparsity and quantization to achieve both high compute and memory efficiency. From our evaluations, we observe that SDQ can achieve 4x effective compute throughput with <1% quality drop.

Abstracting Sparse DNN Acceleration via Structured Sparse Tensor Decomposition

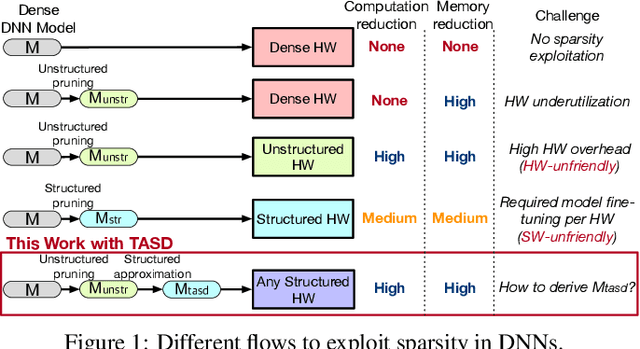
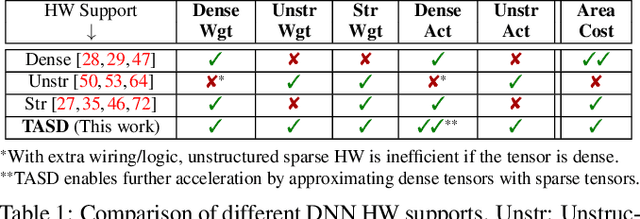
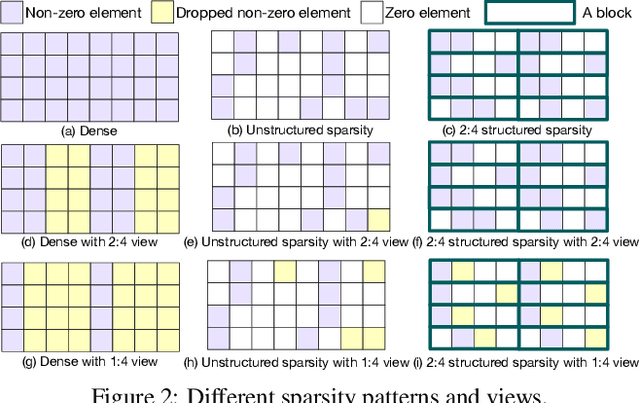
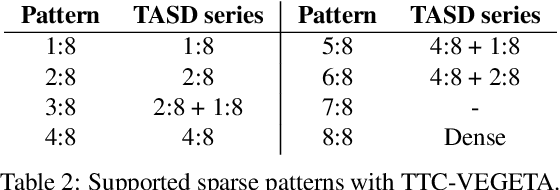
Exploiting sparsity in deep neural networks (DNNs) has been a promising area to meet the growing computation need of modern DNNs. However, in practice, sparse DNN acceleration still faces a key challenge. To minimize the overhead of sparse acceleration, hardware designers have proposed structured sparse hardware support recently, which provides limited flexibility and requires extra model fine-tuning. Moreover, any sparse model fine-tuned for certain structured sparse hardware cannot be accelerated by other structured hardware. To bridge the gap between sparse DNN models and hardware, this paper proposes tensor approximation via structured decomposition (TASD), which leverages the distributive property in linear algebra to turn any sparse tensor into a series of structured sparse tensors. Next, we develop a software framework, TASDER, to accelerate DNNs by searching layer-wise, high-quality structured decomposition for both weight and activation tensors so that they can be accelerated by any systems with structured sparse hardware support. Evaluation results show that, by exploiting prior structured sparse hardware baselines, our method can accelerate off-the-shelf dense and sparse DNNs without fine-tuning and improves energy-delay-product by up to 83% and 74% on average.

HighLight: Efficient and Flexible DNN Acceleration with Hierarchical Structured Sparsity

Due to complex interactions among various deep neural network (DNN) optimization techniques, modern DNNs can have weights and activations that are dense or sparse with diverse sparsity degrees. To offer a good trade-off between accuracy and hardware performance, an ideal DNN accelerator should have high flexibility to efficiently translate DNN sparsity into reductions in energy and/or latency without incurring significant complexity overhead. This paper introduces hierarchical structured sparsity (HSS), with the key insight that we can systematically represent diverse sparsity degrees by having them hierarchically composed from multiple simple sparsity patterns. As a result, HSS simplifies the underlying hardware since it only needs to support simple sparsity patterns; this significantly reduces the sparsity acceleration overhead, which improves efficiency. Motivated by such opportunities, we propose a simultaneously efficient and flexible accelerator, named HighLight, to accelerate DNNs that have diverse sparsity degrees (including dense). Due to the flexibility of HSS, different HSS patterns can be introduced to DNNs to meet different applications' accuracy requirements. Compared to existing works, HighLight achieves a geomean of up to 6.4x better energy-delay product (EDP) across workloads with diverse sparsity degrees, and always sits on the EDP-accuracy Pareto frontier for representative DNNs.

Demystifying Map Space Exploration for NPUs

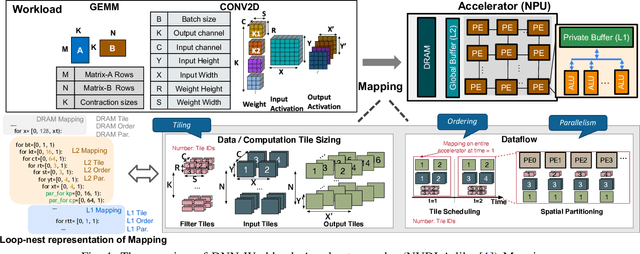
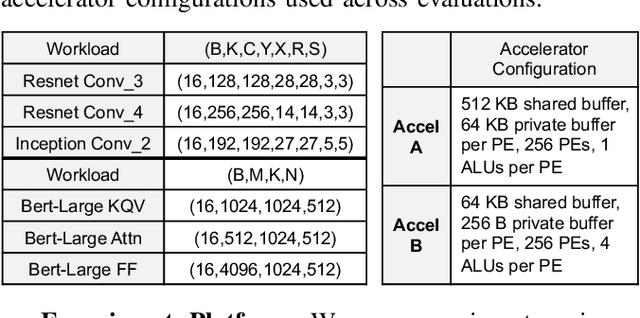
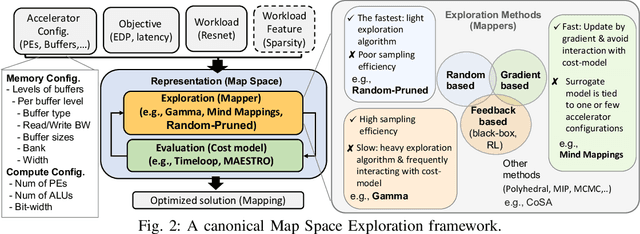
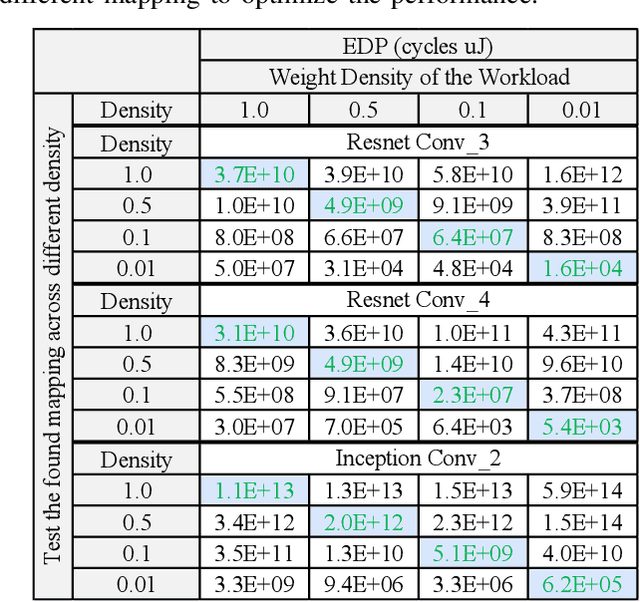
Map Space Exploration is the problem of finding optimized mappings of a Deep Neural Network (DNN) model on an accelerator. It is known to be extremely computationally expensive, and there has been active research looking at both heuristics and learning-based methods to make the problem computationally tractable. However, while there are dozens of mappers out there (all empirically claiming to find better mappings than others), the research community lacks systematic insights on how different search techniques navigate the map-space and how different mapping axes contribute to the accelerator's performance and efficiency. Such insights are crucial to developing mapping frameworks for emerging DNNs that are increasingly irregular (due to neural architecture search) and sparse, making the corresponding map spaces much more complex. In this work, rather than proposing yet another mapper, we do a first-of-its-kind apples-to-apples comparison of search techniques leveraged by different mappers. Next, we extract the learnings from our study and propose two new techniques that can augment existing mappers -- warm-start and sparsity-aware -- that demonstrate speedups, scalability, and robustness across diverse DNN models.

Sparseloop: An Analytical Approach To Sparse Tensor Accelerator Modeling

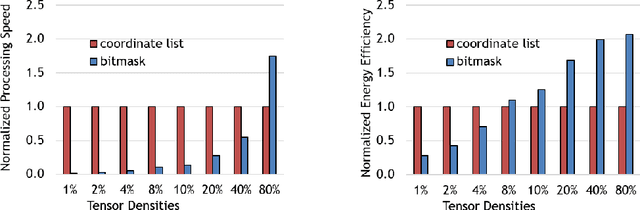
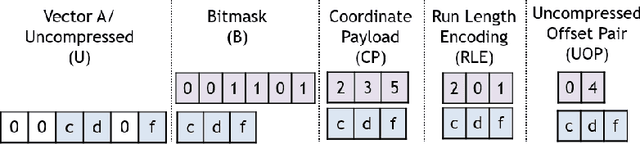
In recent years, many accelerators have been proposed to efficiently process sparse tensor algebra applications (e.g., sparse neural networks). However, these proposals are single points in a large and diverse design space. The lack of systematic description and modeling support for these sparse tensor accelerators impedes hardware designers from efficient and effective design space exploration. This paper first presents a unified taxonomy to systematically describe the diverse sparse tensor accelerator design space. Based on the proposed taxonomy, it then introduces Sparseloop, the first fast, accurate, and flexible analytical modeling framework to enable early-stage evaluation and exploration of sparse tensor accelerators. Sparseloop comprehends a large set of architecture specifications, including various dataflows and sparse acceleration features (e.g., elimination of zero-based compute). Using these specifications, Sparseloop evaluates a design's processing speed and energy efficiency while accounting for data movement and compute incurred by the employed dataflow as well as the savings and overhead introduced by the sparse acceleration features using stochastic tensor density models. Across representative accelerators and workloads, Sparseloop achieves over 2000 times faster modeling speed than cycle-level simulations, maintains relative performance trends, and achieves 0.1% to 8% average error. With a case study, we demonstrate Sparseloop's ability to help reveal important insights for designing sparse tensor accelerators (e.g., it is important to co-design orthogonal design aspects).

Union: A Unified HW-SW Co-Design Ecosystem in MLIR for Evaluating Tensor Operations on Spatial Accelerators

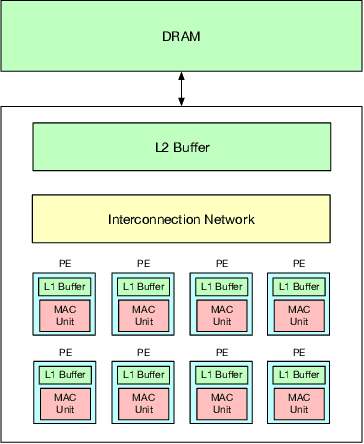
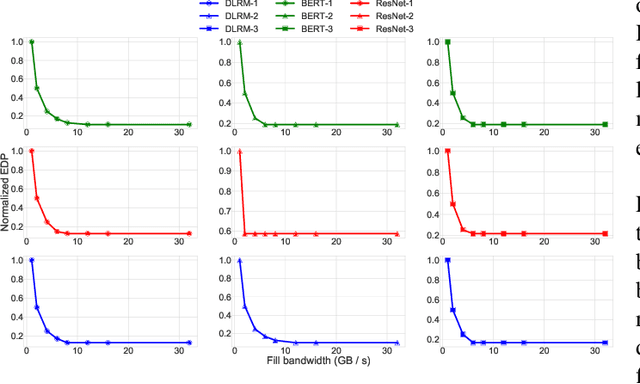
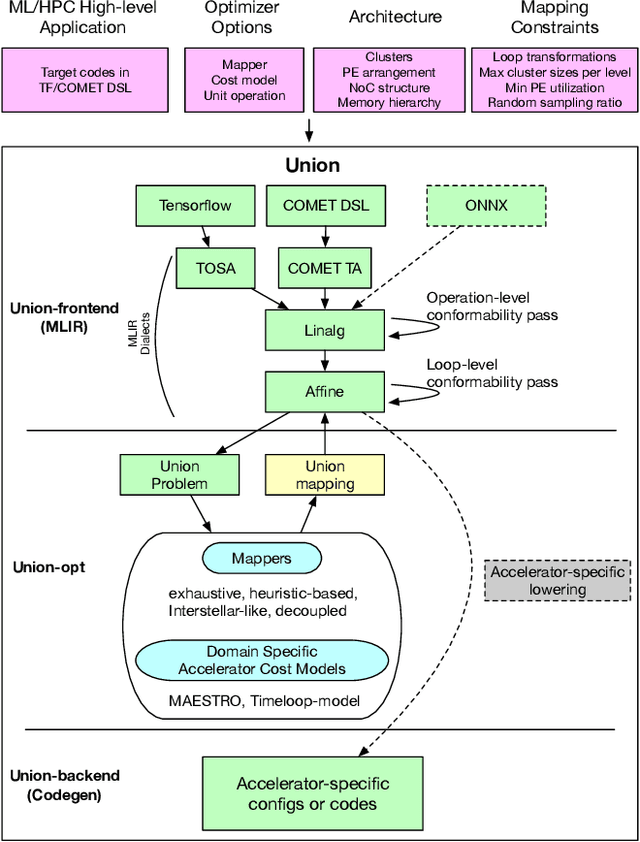
To meet the extreme compute demands for deep learning across commercial and scientific applications, dataflow accelerators are becoming increasingly popular. While these "domain-specific" accelerators are not fully programmable like CPUs and GPUs, they retain varying levels of flexibility with respect to data orchestration, i.e., dataflow and tiling optimizations to enhance efficiency. There are several challenges when designing new algorithms and mapping approaches to execute the algorithms for a target problem on new hardware. Previous works have addressed these challenges individually. To address this challenge as a whole, in this work, we present a HW-SW co-design ecosystem for spatial accelerators called Union within the popular MLIR compiler infrastructure. Our framework allows exploring different algorithms and their mappings on several accelerator cost models. Union also includes a plug-and-play library of accelerator cost models and mappers which can easily be extended. The algorithms and accelerator cost models are connected via a novel mapping abstraction that captures the map space of spatial accelerators which can be systematically pruned based on constraints from the hardware, workload, and mapper. We demonstrate the value of Union for the community with several case studies which examine offloading different tensor operations(CONV/GEMM/Tensor Contraction) on diverse accelerator architectures using different mapping schemes.

Mind Mappings: Enabling Efficient Algorithm-Accelerator Mapping Space Search

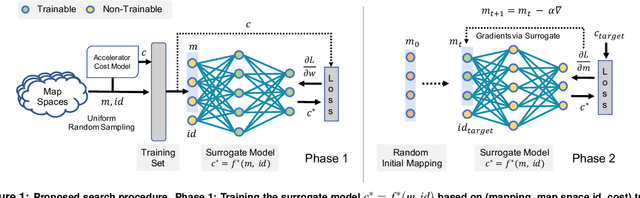
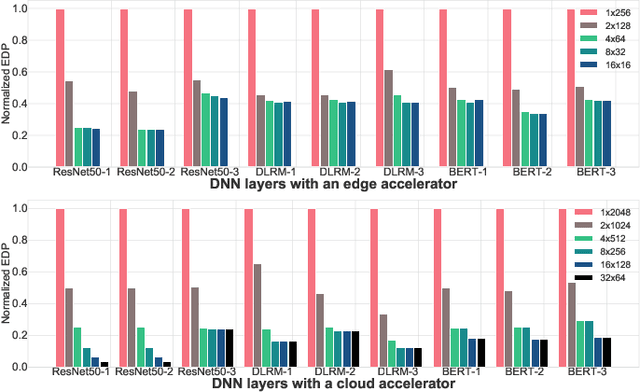
Modern day computing increasingly relies on specialization to satiate growing performance and efficiency requirements. A core challenge in designing such specialized hardware architectures is how to perform mapping space search, i.e., search for an optimal mapping from algorithm to hardware. Prior work shows that choosing an inefficient mapping can lead to multiplicative-factor efficiency overheads. Additionally, the search space is not only large but also non-convex and non-smooth, precluding advanced search techniques. As a result, previous works are forced to implement mapping space search using expert choices or sub-optimal search heuristics. This work proposes Mind Mappings, a novel gradient-based search method for algorithm-accelerator mapping space search. The key idea is to derive a smooth, differentiable approximation to the otherwise non-smooth, non-convex search space. With a smooth, differentiable approximation, we can leverage efficient gradient-based search algorithms to find high-quality mappings. We extensively compare Mind Mappings to black-box optimization schemes used in prior work. When tasked to find mappings for two important workloads (CNN and MTTKRP), the proposed search finds mappings that achieve an average $1.40\times$, $1.76\times$, and $1.29\times$ (when run for a fixed number of steps) and $3.16\times$, $4.19\times$, and $2.90\times$ (when run for a fixed amount of time) better energy-delay product (EDP) relative to Simulated Annealing, Genetic Algorithms and Reinforcement Learning, respectively. Meanwhile, Mind Mappings returns mappings with only $5.32\times$ higher EDP than a possibly unachievable theoretical lower-bound, indicating proximity to the global optima.