Mind Mappings: Enabling Efficient Algorithm-Accelerator Mapping Space Search
Paper and Code
Mar 02, 2021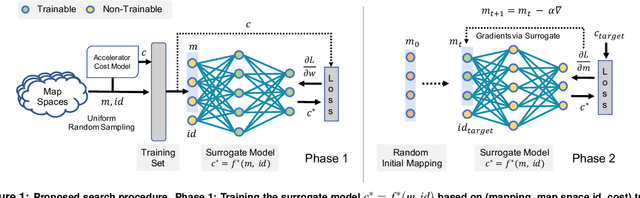
Modern day computing increasingly relies on specialization to satiate growing performance and efficiency requirements. A core challenge in designing such specialized hardware architectures is how to perform mapping space search, i.e., search for an optimal mapping from algorithm to hardware. Prior work shows that choosing an inefficient mapping can lead to multiplicative-factor efficiency overheads. Additionally, the search space is not only large but also non-convex and non-smooth, precluding advanced search techniques. As a result, previous works are forced to implement mapping space search using expert choices or sub-optimal search heuristics. This work proposes Mind Mappings, a novel gradient-based search method for algorithm-accelerator mapping space search. The key idea is to derive a smooth, differentiable approximation to the otherwise non-smooth, non-convex search space. With a smooth, differentiable approximation, we can leverage efficient gradient-based search algorithms to find high-quality mappings. We extensively compare Mind Mappings to black-box optimization schemes used in prior work. When tasked to find mappings for two important workloads (CNN and MTTKRP), the proposed search finds mappings that achieve an average $1.40\times$, $1.76\times$, and $1.29\times$ (when run for a fixed number of steps) and $3.16\times$, $4.19\times$, and $2.90\times$ (when run for a fixed amount of time) better energy-delay product (EDP) relative to Simulated Annealing, Genetic Algorithms and Reinforcement Learning, respectively. Meanwhile, Mind Mappings returns mappings with only $5.32\times$ higher EDP than a possibly unachievable theoretical lower-bound, indicating proximity to the global optima.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge