Materials Learning Algorithms (MALA): Scalable Machine Learning for Electronic Structure Calculations in Large-Scale Atomistic Simulations

We present the Materials Learning Algorithms (MALA) package, a scalable machine learning framework designed to accelerate density functional theory (DFT) calculations suitable for large-scale atomistic simulations. Using local descriptors of the atomic environment, MALA models efficiently predict key electronic observables, including local density of states, electronic density, density of states, and total energy. The package integrates data sampling, model training and scalable inference into a unified library, while ensuring compatibility with standard DFT and molecular dynamics codes. We demonstrate MALA's capabilities with examples including boron clusters, aluminum across its solid-liquid phase boundary, and predicting the electronic structure of a stacking fault in a large beryllium slab. Scaling analyses reveal MALA's computational efficiency and identify bottlenecks for future optimization. With its ability to model electronic structures at scales far beyond standard DFT, MALA is well suited for modeling complex material systems, making it a versatile tool for advanced materials research.

Accelerating Electron Dynamics Simulations through Machine Learned Time Propagators

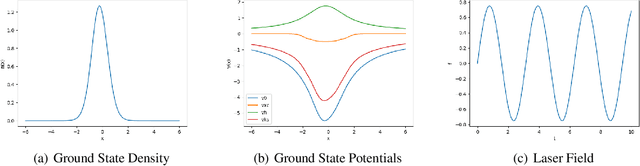
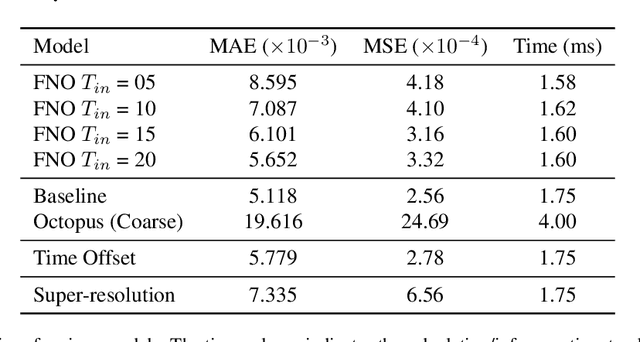
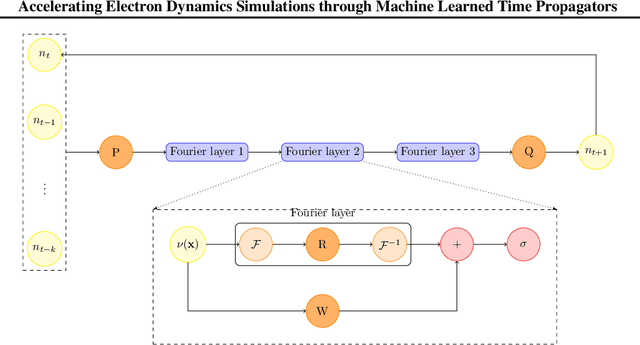
Time-dependent density functional theory (TDDFT) is a widely used method to investigate electron dynamics under various external perturbations such as laser fields. In this work, we present a novel approach to accelerate real time TDDFT based electron dynamics simulations using autoregressive neural operators as time-propagators for the electron density. By leveraging physics-informed constraints and high-resolution training data, our model achieves superior accuracy and computational speed compared to traditional numerical solvers. We demonstrate the effectiveness of our model on a class of one-dimensional diatomic molecules. This method has potential in enabling real-time, on-the-fly modeling of laser-irradiated molecules and materials with varying experimental parameters.

A Scalable 5,6-Qubit Grover's Quantum Search Algorithm

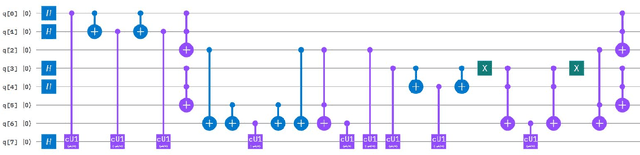
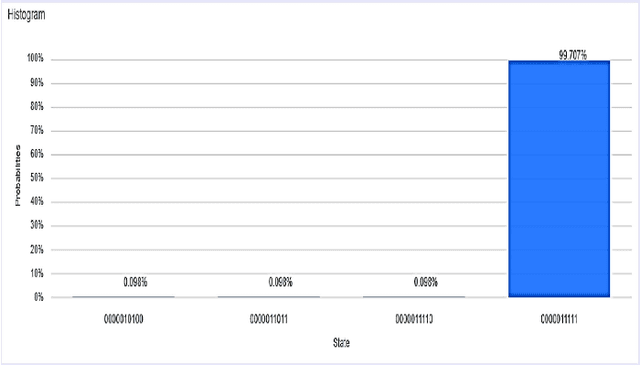
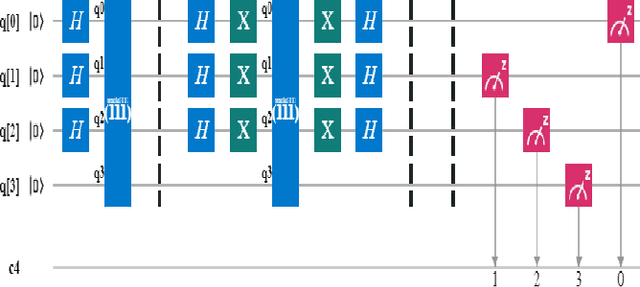
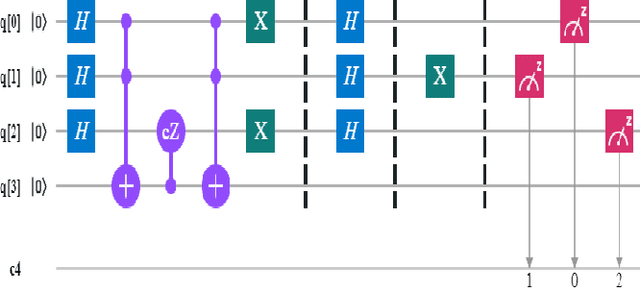
Recent studies have been spurred on by the promise of advanced quantum computing technology, which has led to the development of quantum computer simulations on classical hardware. Grover's quantum search algorithm is one of the well-known applications of quantum computing, enabling quantum computers to perform a database search (unsorted array) and quadratically outperform their classical counterparts in terms of time. Given the restricted access to database search for an oracle model (black-box), researchers have demonstrated various implementations of Grover's circuit for two to four qubits on various platforms. However, larger search spaces have not yet been explored. In this paper, a scalable Quantum Grover Search algorithm is introduced and implemented using 5-qubit and 6-qubit quantum circuits, along with a design pattern for ease of building an Oracle for a higher order of qubits. For our implementation, the probability of finding the correct entity is in the high nineties. The accuracy of the proposed 5-qubit and 6-qubit circuits is benchmarked against the state-of-the-art implementations for 3-qubit and 4-qubit. Furthermore, the reusability of the proposed quantum circuits using subroutines is also illustrated by the opportunity for large-scale implementation of quantum algorithms in the future.

Random Quantum Neural Networks (RQNN) for Noisy Image Recognition

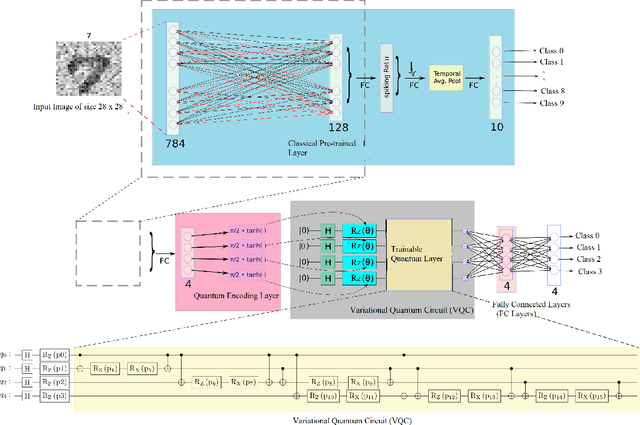
Classical Random Neural Networks (RNNs) have demonstrated effective applications in decision making, signal processing, and image recognition tasks. However, their implementation has been limited to deterministic digital systems that output probability distributions in lieu of stochastic behaviors of random spiking signals. We introduce the novel class of supervised Random Quantum Neural Networks (RQNNs) with a robust training strategy to better exploit the random nature of the spiking RNN. The proposed RQNN employs hybrid classical-quantum algorithms with superposition state and amplitude encoding features, inspired by quantum information theory and the brain's spatial-temporal stochastic spiking property of neuron information encoding. We have extensively validated our proposed RQNN model, relying on hybrid classical-quantum algorithms via the PennyLane Quantum simulator with a limited number of \emph{qubits}. Experiments on the MNIST, FashionMNIST, and KMNIST datasets demonstrate that the proposed RQNN model achieves an average classification accuracy of $94.9\%$. Additionally, the experimental findings illustrate the proposed RQNN's effectiveness and resilience in noisy settings, with enhanced image classification accuracy when compared to the classical counterparts (RNNs), classical Spiking Neural Networks (SNNs), and the classical convolutional neural network (AlexNet). Furthermore, the RQNN can deal with noise, which is useful for various applications, including computer vision in NISQ devices. The PyTorch code (https://github.com/darthsimpus/RQN) is made available on GitHub to reproduce the results reported in this manuscript.

Accelerating Finite-temperature Kohn-Sham Density Functional Theory with Deep Neural Networks

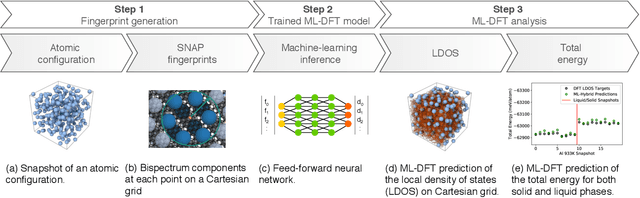
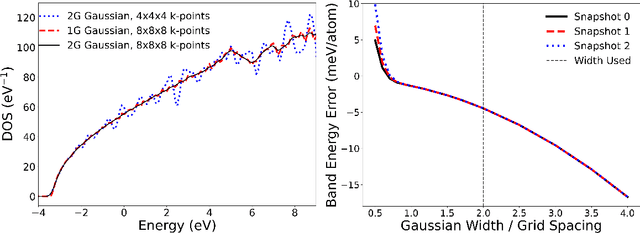
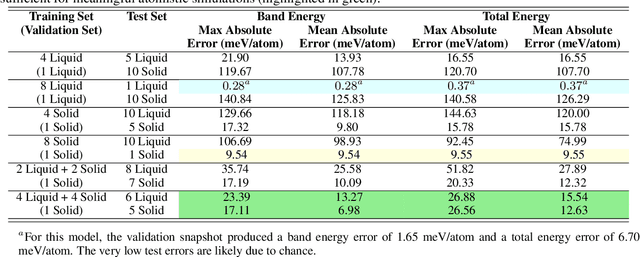
We present a numerical modeling workflow based on machine learning (ML) which reproduces the the total energies produced by Kohn-Sham density functional theory (DFT) at finite electronic temperature to within chemical accuracy at negligible computational cost. Based on deep neural networks, our workflow yields the local density of states (LDOS) for a given atomic configuration. From the LDOS, spatially-resolved, energy-resolved, and integrated quantities can be calculated, including the DFT total free energy, which serves as the Born-Oppenheimer potential energy surface for the atoms. We demonstrate the efficacy of this approach for both solid and liquid metals and compare results between independent and unified machine-learning models for solid and liquid aluminum. Our machine-learning density functional theory framework opens up the path towards multiscale materials modeling for matter under ambient and extreme conditions at a computational scale and cost that is unattainable with current algorithms.