Gordon E. Moon
Evaluating Spatial Accelerator Architectures with Tiled Matrix-Matrix Multiplication
Jun 19, 2021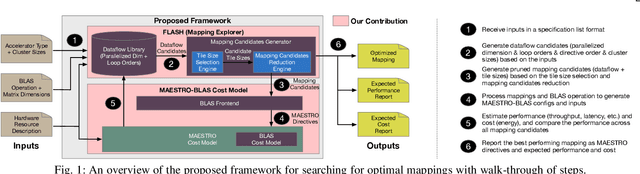
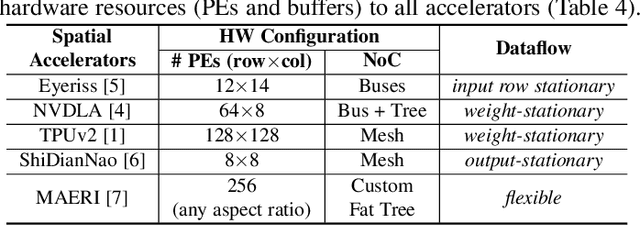
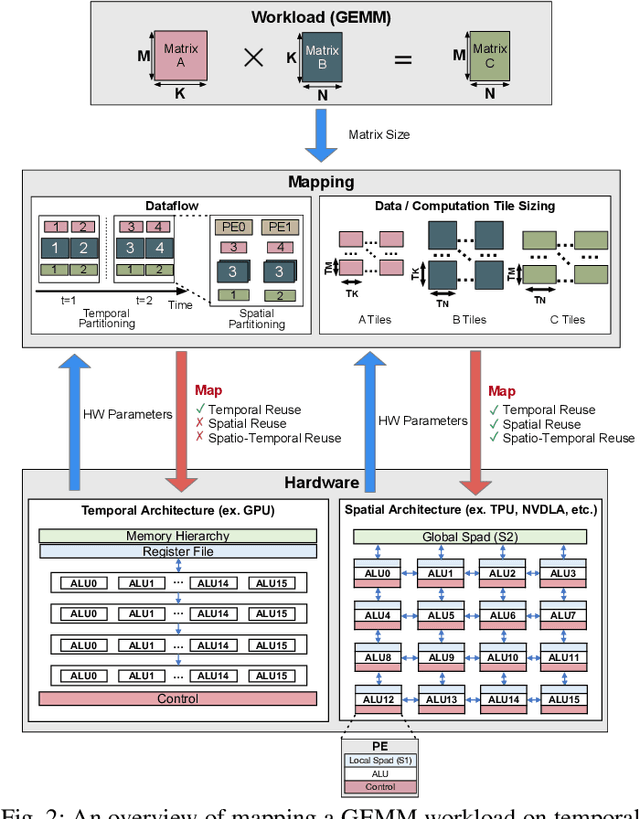

Abstract:There is a growing interest in custom spatial accelerators for machine learning applications. These accelerators employ a spatial array of processing elements (PEs) interacting via custom buffer hierarchies and networks-on-chip. The efficiency of these accelerators comes from employing optimized dataflow (i.e., spatial/temporal partitioning of data across the PEs and fine-grained scheduling) strategies to optimize data reuse. The focus of this work is to evaluate these accelerator architectures using a tiled general matrix-matrix multiplication (GEMM) kernel. To do so, we develop a framework that finds optimized mappings (dataflow and tile sizes) for a tiled GEMM for a given spatial accelerator and workload combination, leveraging an analytical cost model for runtime and energy. Our evaluations over five spatial accelerators demonstrate that the tiled GEMM mappings systematically generated by our framework achieve high performance on various GEMM workloads and accelerators.
PL-NMF: Parallel Locality-Optimized Non-negative Matrix Factorization
Apr 16, 2019
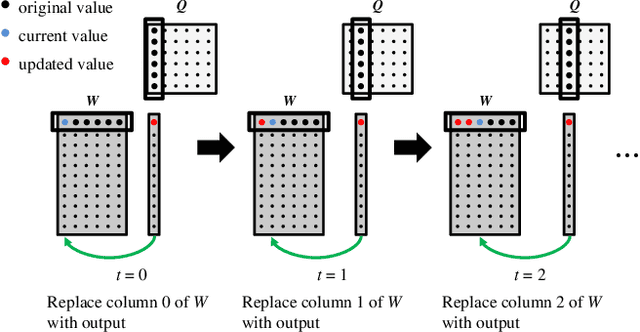
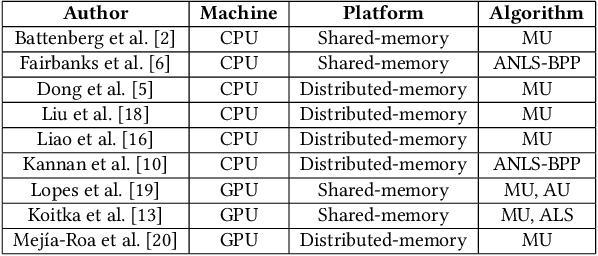
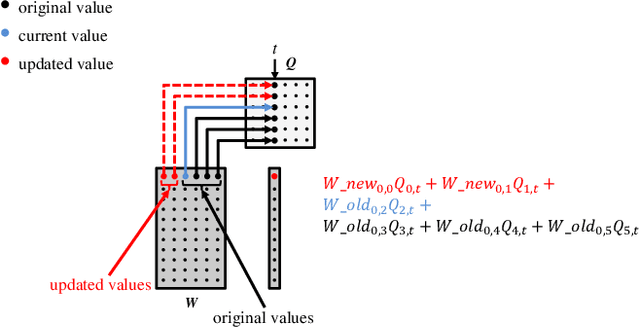
Abstract:Non-negative Matrix Factorization (NMF) is a key kernel for unsupervised dimension reduction used in a wide range of applications, including topic modeling, recommender systems and bioinformatics. Due to the compute-intensive nature of applications that must perform repeated NMF, several parallel implementations have been developed in the past. However, existing parallel NMF algorithms have not addressed data locality optimizations, which are critical for high performance since data movement costs greatly exceed the cost of arithmetic/logic operations on current computer systems. In this paper, we devise a parallel NMF algorithm based on the HALS (Hierarchical Alternating Least Squares) scheme that incorporates algorithmic transformations to enhance data locality. Efficient realizations of the algorithm on multi-core CPUs and GPUs are developed, demonstrating significant performance improvement over existing state-of-the-art parallel NMF algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge