What Operations can be Performed Directly on Compressed Arrays, and with What Error?

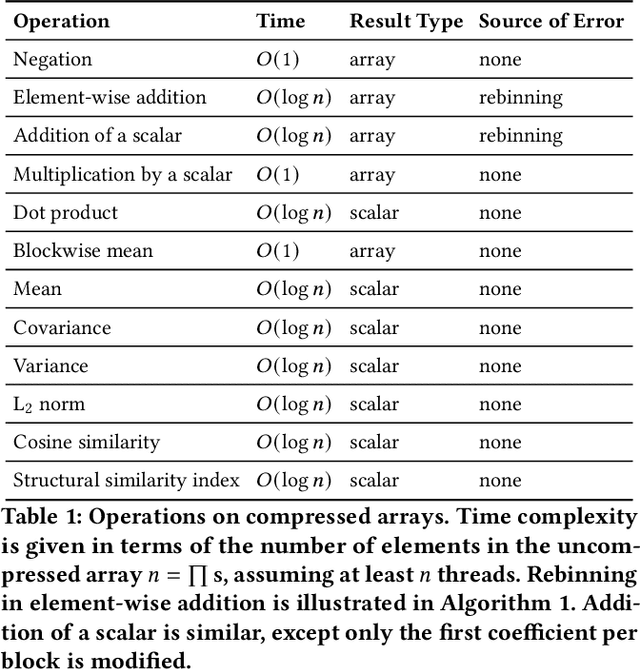
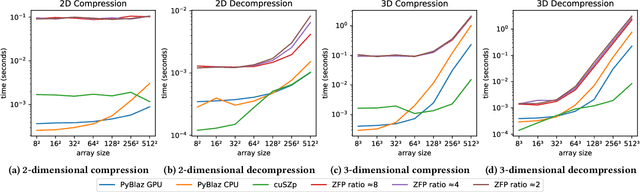
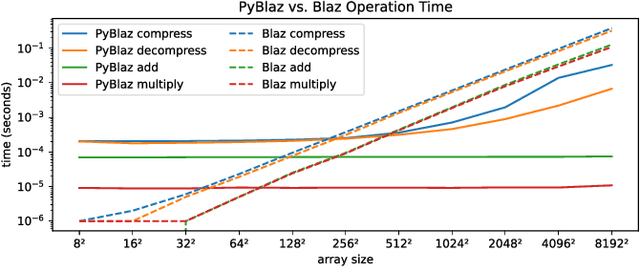
In response to the rapidly escalating costs of computing with large matrices and tensors caused by data movement, several lossy compression methods have been developed to significantly reduce data volumes. Unfortunately, all these methods require the data to be decompressed before further computations are done. In this work, we develop a lossy compressor that allows a dozen fairly fundamental operations directly on compressed data while offering good compression ratios and modest errors. We implement a new compressor PyBlaz based on the familiar GPU-powered PyTorch framework, and evaluate it on three non-trivial applications, choosing different number systems for internal representation. Our results demonstrate that the compressed-domain operations achieve good scalability with problem sizes while incurring errors well within acceptable limits. To our best knowledge, this is the first such lossy compressor that supports compressed-domain operations while achieving acceptable performance as well as error.

An Empirical Investigation of Matrix Factorization Methods for Pre-trained Transformers

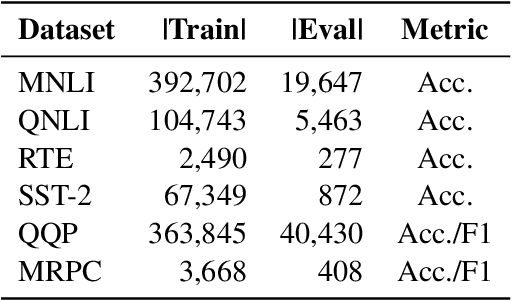
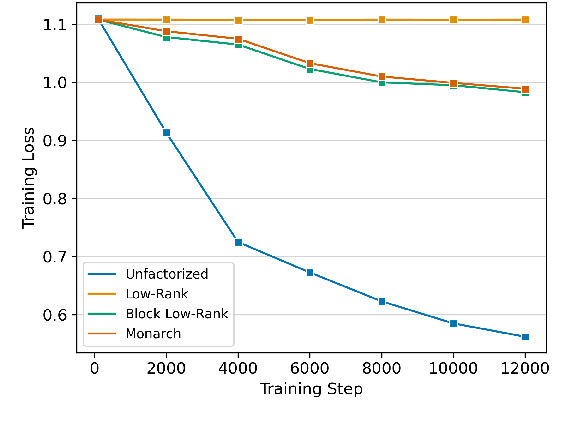
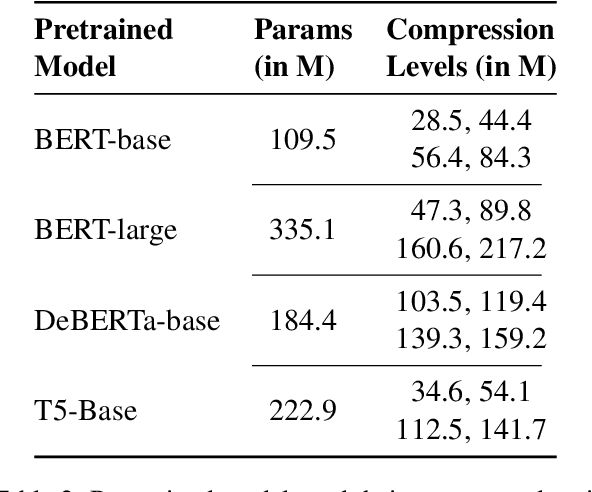
The increasing size of transformer-based models in NLP makes the question of compressing them important. In this work, we present a comprehensive analysis of factorization based model compression techniques. Specifically, we focus on comparing straightforward low-rank factorization against the recently introduced Monarch factorization, which exhibits impressive performance preservation on the GLUE benchmark. To mitigate stability issues associated with low-rank factorization of the matrices in pre-trained transformers, we introduce a staged factorization approach wherein layers are factorized one by one instead of being factorized simultaneously. Through this strategy we significantly enhance the stability and reliability of the compression process. Further, we introduce a simple block-wise low-rank factorization method, which has a close relationship to Monarch factorization. Our experiments lead to the surprising conclusion that straightforward low-rank factorization consistently outperforms Monarch factorization across both different compression ratios and six different text classification tasks.

Analytical Characterization and Design Space Exploration for Optimization of CNNs

Moving data through the memory hierarchy is a fundamental bottleneck that can limit the performance of core algorithms of machine learning, such as convolutional neural networks (CNNs). Loop-level optimization, including loop tiling and loop permutation, are fundamental transformations to reduce data movement. However, the search space for finding the best loop-level optimization configuration is explosively large. This paper develops an analytical modeling approach for finding the best loop-level optimization configuration for CNNs on multi-core CPUs. Experimental evaluation shows that this approach achieves comparable or better performance than state-of-the-art libraries and auto-tuning based optimizers for CNNs.

PL-NMF: Parallel Locality-Optimized Non-negative Matrix Factorization

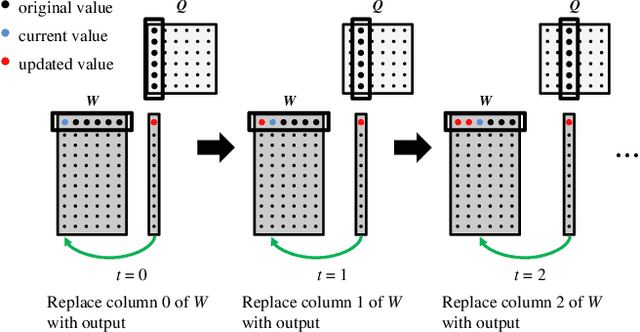
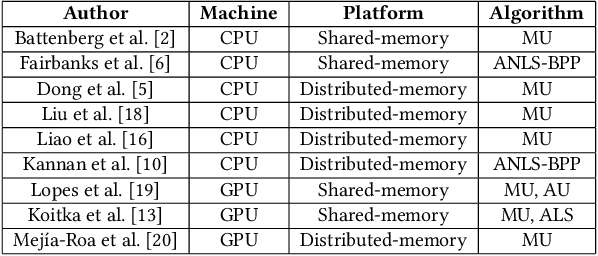
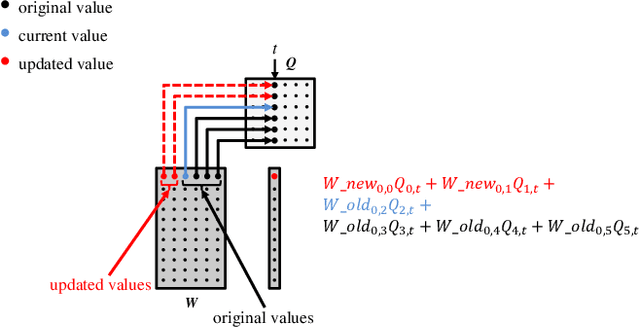
Non-negative Matrix Factorization (NMF) is a key kernel for unsupervised dimension reduction used in a wide range of applications, including topic modeling, recommender systems and bioinformatics. Due to the compute-intensive nature of applications that must perform repeated NMF, several parallel implementations have been developed in the past. However, existing parallel NMF algorithms have not addressed data locality optimizations, which are critical for high performance since data movement costs greatly exceed the cost of arithmetic/logic operations on current computer systems. In this paper, we devise a parallel NMF algorithm based on the HALS (Hierarchical Alternating Least Squares) scheme that incorporates algorithmic transformations to enhance data locality. Efficient realizations of the algorithm on multi-core CPUs and GPUs are developed, demonstrating significant performance improvement over existing state-of-the-art parallel NMF algorithms.

ATP: Directed Graph Embedding with Asymmetric Transitivity Preservation

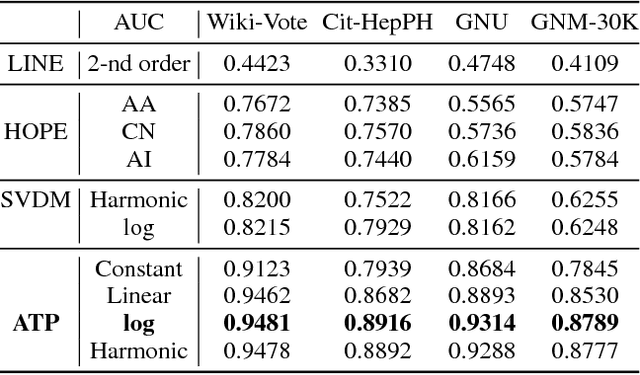
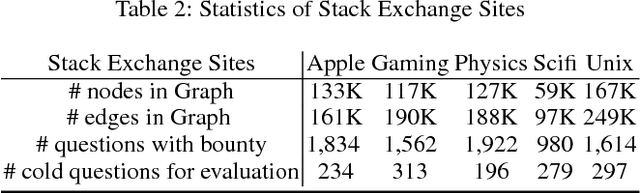
Directed graphs have been widely used in Community Question Answering services (CQAs) to model asymmetric relationships among different types of nodes in CQA graphs, e.g., question, answer, user. Asymmetric transitivity is an essential property of directed graphs, since it can play an important role in downstream graph inference and analysis. Question difficulty and user expertise follow the characteristic of asymmetric transitivity. Maintaining such properties, while reducing the graph to a lower dimensional vector embedding space, has been the focus of much recent research. In this paper, we tackle the challenge of directed graph embedding with asymmetric transitivity preservation and then leverage the proposed embedding method to solve a fundamental task in CQAs: how to appropriately route and assign newly posted questions to users with the suitable expertise and interest in CQAs. The technique incorporates graph hierarchy and reachability information naturally by relying on a non-linear transformation that operates on the core reachability and implicit hierarchy within such graphs. Subsequently, the methodology levers a factorization-based approach to generate two embedding vectors for each node within the graph, to capture the asymmetric transitivity. Extensive experiments show that our framework consistently and significantly outperforms the state-of-the-art baselines on two diverse real-world tasks: link prediction, and question difficulty estimation and expert finding in online forums like Stack Exchange. Particularly, our framework can support inductive embedding learning for newly posted questions (unseen nodes during training), and therefore can properly route and assign these kinds of questions to experts in CQAs.