What Operations can be Performed Directly on Compressed Arrays, and with What Error?

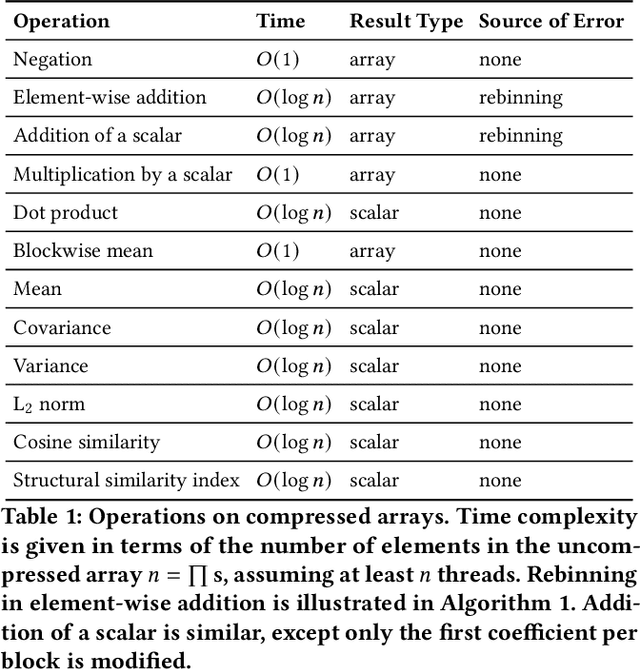
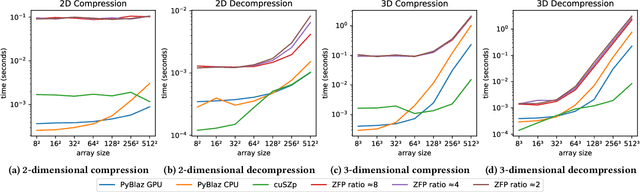
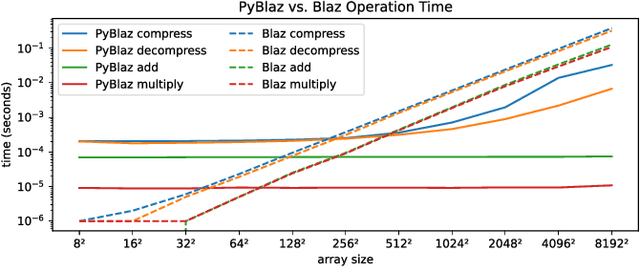
In response to the rapidly escalating costs of computing with large matrices and tensors caused by data movement, several lossy compression methods have been developed to significantly reduce data volumes. Unfortunately, all these methods require the data to be decompressed before further computations are done. In this work, we develop a lossy compressor that allows a dozen fairly fundamental operations directly on compressed data while offering good compression ratios and modest errors. We implement a new compressor PyBlaz based on the familiar GPU-powered PyTorch framework, and evaluate it on three non-trivial applications, choosing different number systems for internal representation. Our results demonstrate that the compressed-domain operations achieve good scalability with problem sizes while incurring errors well within acceptable limits. To our best knowledge, this is the first such lossy compressor that supports compressed-domain operations while achieving acceptable performance as well as error.

Understanding the Effect of the Long Tail on Neural Network Compression

Network compression is now a mature sub-field of neural network research: over the last decade, significant progress has been made towards reducing the size of models and speeding up inference, while maintaining the classification accuracy. However, many works have observed that focusing on just the overall accuracy can be misguided. E.g., it has been shown that mismatches between the full and compressed models can be biased towards under-represented classes. This raises the important research question, can we achieve network compression while maintaining "semantic equivalence" with the original network? In this work, we study this question in the context of the "long tail" phenomenon in computer vision datasets observed by Feldman, et al. They argue that memorization of certain inputs (appropriately defined) is essential to achieving good generalization. As compression limits the capacity of a network (and hence also its ability to memorize), we study the question: are mismatches between the full and compressed models correlated with the memorized training data? We present positive evidence in this direction for image classification tasks, by considering different base architectures and compression schemes.

Reliable Model Compression via Label-Preservation-Aware Loss Functions

Model compression is a ubiquitous tool that brings the power of modern deep learning to edge devices with power and latency constraints. The goal of model compression is to take a large reference neural network and output a smaller and less expensive compressed network that is functionally equivalent to the reference. Compression typically involves pruning and/or quantization, followed by re-training to maintain the reference accuracy. However, it has been observed that compression can lead to a considerable mismatch in the labels produced by the reference and the compressed models, resulting in bias and unreliability. To combat this, we present a framework that uses a teacher-student learning paradigm to better preserve labels. We investigate the role of additional terms to the loss function and show how to automatically tune the associated parameters. We demonstrate the effectiveness of our approach both quantitatively and qualitatively on multiple compression schemes and accuracy recovery algorithms using a set of 8 different real-world network architectures. We obtain a significant reduction of up to 4.1X in the number of mismatches between the compressed and reference models, and up to 5.7X in cases where the reference model makes the correct prediction.

A Programmable Approach to Model Compression

Deep neural networks frequently contain far more weights, represented at a higher precision, than are required for the specific task which they are trained to perform. Consequently, they can often be compressed using techniques such as weight pruning and quantization that reduce both model size and inference time without appreciable loss in accuracy. Compressing models before they are deployed can therefore result in significantly more efficient systems. However, while the results are desirable, finding the best compression strategy for a given neural network, target platform, and optimization objective often requires extensive experimentation. Moreover, finding optimal hyperparameters for a given compression strategy typically results in even more expensive, frequently manual, trial-and-error exploration. In this paper, we introduce a programmable system for model compression called Condensa. Users programmatically compose simple operators, in Python, to build complex compression strategies. Given a strategy and a user-provided objective, such as minimization of running time, Condensa uses a novel sample-efficient constrained Bayesian optimization algorithm to automatically infer desirable sparsity ratios. Our experiments on three real-world image classification and language modeling tasks demonstrate memory footprint reductions of up to 65x and runtime throughput improvements of up to 2.22x using at most 10 samples per search. We have released a reference implementation of Condensa at https://github.com/NVlabs/condensa.

Message Scheduling for Performant, Many-Core Belief Propagation

Belief Propagation (BP) is a message-passing algorithm for approximate inference over Probabilistic Graphical Models (PGMs), finding many applications such as computer vision, error-correcting codes, and protein-folding. While general, the convergence and speed of the algorithm has limited its practical use on difficult inference problems. As an algorithm that is highly amenable to parallelization, many-core Graphical Processing Units (GPUs) could significantly improve BP performance. Improving BP through many-core systems is non-trivial: the scheduling of messages in the algorithm strongly affects performance. We present a study of message scheduling for BP on GPUs. We demonstrate that BP exhibits a tradeoff between speed and convergence based on parallelism and show that existing message schedulings are not able to utilize this tradeoff. To this end, we present a novel randomized message scheduling approach, Randomized BP (RnBP), which outperforms existing methods on the GPU.