What Operations can be Performed Directly on Compressed Arrays, and with What Error?

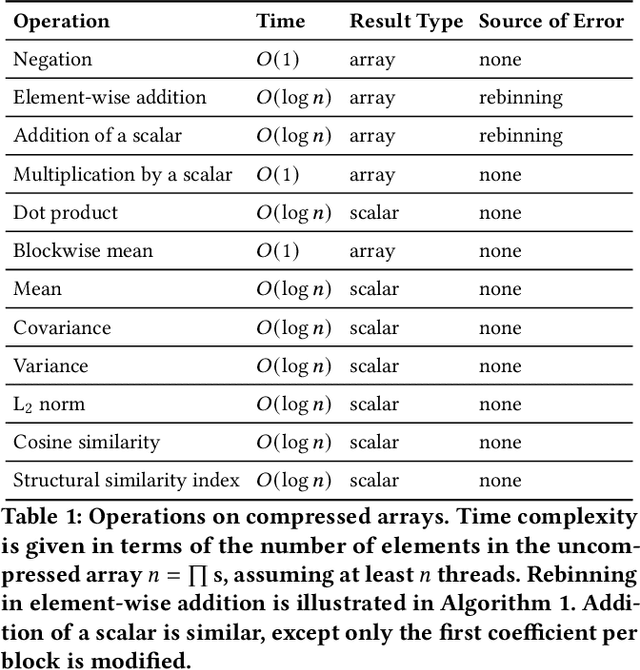
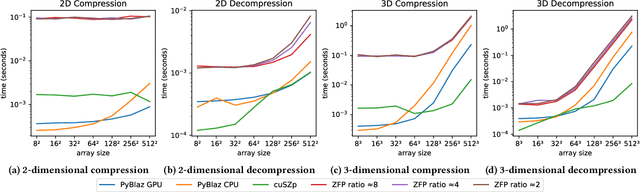
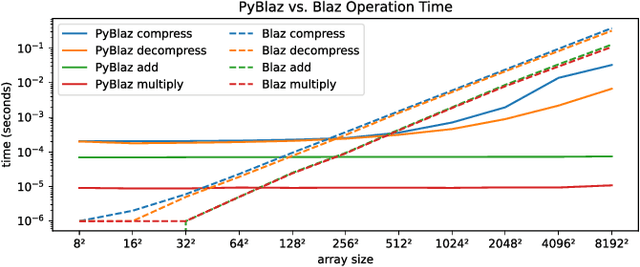
In response to the rapidly escalating costs of computing with large matrices and tensors caused by data movement, several lossy compression methods have been developed to significantly reduce data volumes. Unfortunately, all these methods require the data to be decompressed before further computations are done. In this work, we develop a lossy compressor that allows a dozen fairly fundamental operations directly on compressed data while offering good compression ratios and modest errors. We implement a new compressor PyBlaz based on the familiar GPU-powered PyTorch framework, and evaluate it on three non-trivial applications, choosing different number systems for internal representation. Our results demonstrate that the compressed-domain operations achieve good scalability with problem sizes while incurring errors well within acceptable limits. To our best knowledge, this is the first such lossy compressor that supports compressed-domain operations while achieving acceptable performance as well as error.

An Efficient Summation Algorithm for the Accuracy, Convergence and Reproducibility of Parallel Numerical Methods

Nowadays, parallel computing is ubiquitous in several application fields, both in engineering and science. The computations rely on the floating-point arithmetic specified by the IEEE754 Standard. In this context, an elementary brick of computation, used everywhere, is the sum of a sequence of numbers. This sum is subject to many numerical errors in floating-point arithmetic. To alleviate this issue, we have introduced a new parallel algorithm for summing a sequence of floating-point numbers. This algorithm which scales up easily with the number of processors, adds numbers of the same exponents first. In this article, our main contribution is an extensive analysis of its efficiency with respect to several properties: accuracy, convergence and reproducibility. In order to show the usefulness of our algorithm, we have chosen a set of representative numerical methods which are Simpson, Jacobi, LU factorization and the Iterated power method.

Fixed-Point Code Synthesis For Neural Networks

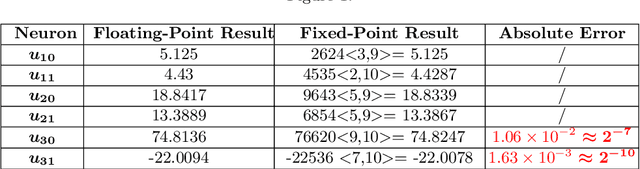
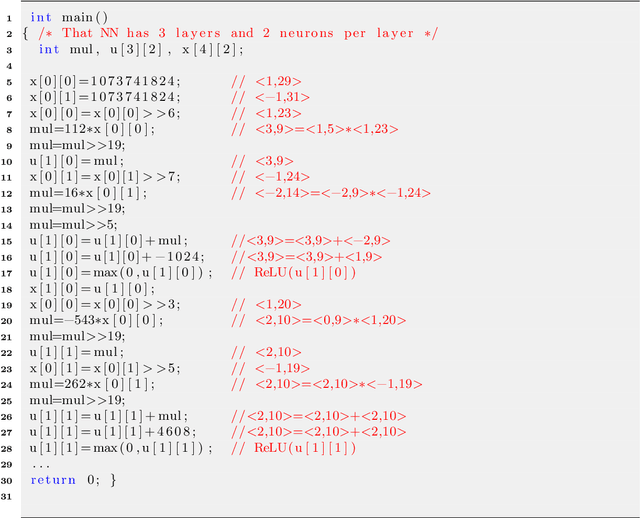
Over the last few years, neural networks have started penetrating safety critical systems to take decisions in robots, rockets, autonomous driving car, etc. A problem is that these critical systems often have limited computing resources. Often, they use the fixed-point arithmetic for its many advantages (rapidity, compatibility with small memory devices.) In this article, a new technique is introduced to tune the formats (precision) of already trained neural networks using fixed-point arithmetic, which can be implemented using integer operations only. The new optimized neural network computes the output with fixed-point numbers without modifying the accuracy up to a threshold fixed by the user. A fixed-point code is synthesized for the new optimized neural network ensuring the respect of the threshold for any input vector belonging the range [xmin, xmax] determined during the analysis. From a technical point of view, we do a preliminary analysis of our floating neural network to determine the worst cases, then we generate a system of linear constraints among integer variables that we can solve by linear programming. The solution of this system is the new fixed-point format of each neuron. The experimental results obtained show the efficiency of our method which can ensure that the new fixed-point neural network has the same behavior as the initial floating-point neural network.