Directional Sign Loss: A Topology-Preserving Loss Function that Approximates the Sign of Finite Differences

Preserving critical topological features in learned latent spaces is a fundamental challenge in representation learning, particularly for topology-sensitive data. This paper introduces directional sign loss (DSL), a novel loss function that approximates the number of mismatches in the signs of finite differences between corresponding elements of two arrays. By penalizing discrepancies in critical points between input and reconstructed data, DSL encourages autoencoders and other learnable compressors to retain the topological features of the original data. We present the mathematical formulation, complexity analysis, and practical implementation of DSL, comparing its behavior to its non-differentiable counterpart and to other topological measures. Experiments on one-, two-, and three-dimensional data show that combining DSL with traditional loss functions preserves topological features more effectively than traditional losses alone. Moreover, DSL serves as a differentiable, efficient proxy for common topology-based metrics, enabling its use in gradient-based optimization frameworks.

What Operations can be Performed Directly on Compressed Arrays, and with What Error?

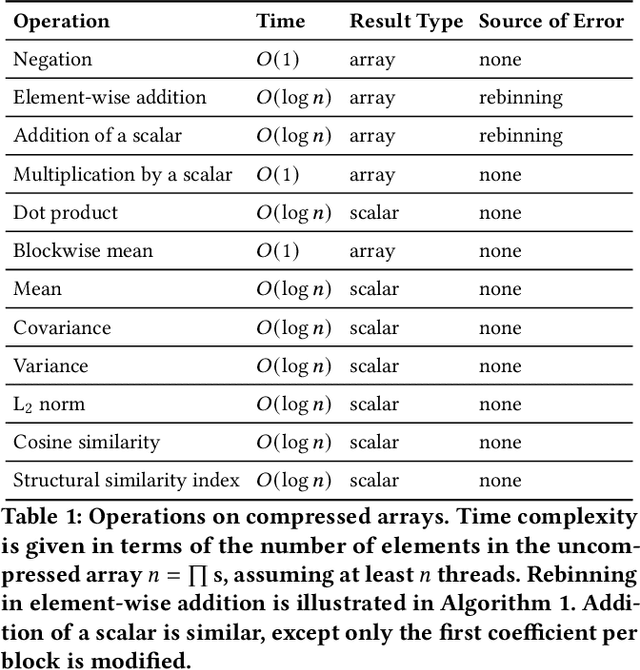
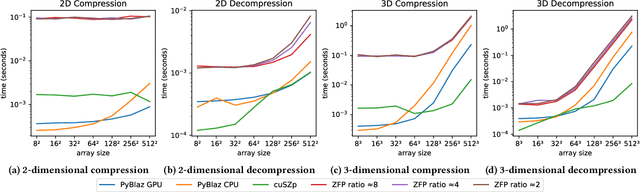
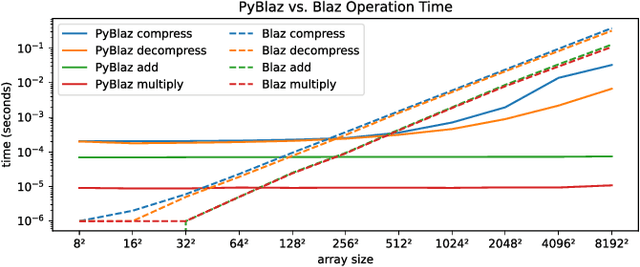
In response to the rapidly escalating costs of computing with large matrices and tensors caused by data movement, several lossy compression methods have been developed to significantly reduce data volumes. Unfortunately, all these methods require the data to be decompressed before further computations are done. In this work, we develop a lossy compressor that allows a dozen fairly fundamental operations directly on compressed data while offering good compression ratios and modest errors. We implement a new compressor PyBlaz based on the familiar GPU-powered PyTorch framework, and evaluate it on three non-trivial applications, choosing different number systems for internal representation. Our results demonstrate that the compressed-domain operations achieve good scalability with problem sizes while incurring errors well within acceptable limits. To our best knowledge, this is the first such lossy compressor that supports compressed-domain operations while achieving acceptable performance as well as error.