Robust Gaussian Process Regression for Real-Time High Precision GPS Signal Enhancement

Satellite-based positioning system such as GPS often suffers from large amount of noise that degrades the positioning accuracy dramatically especially in real-time applications. In this work, we consider a data-mining approach to enhance the GPS signal. We build a large-scale high precision GPS receiver grid system to collect real-time GPS signals for training. The Gaussian Process (GP) regression is chosen to model the vertical Total Electron Content (vTEC) distribution of the ionosphere of the Earth. Our experiments show that the noise in the real-time GPS signals often exceeds the breakdown point of the conventional robust regression methods resulting in sub-optimal system performance. We propose a three-step approach to address this challenge. In the first step we perform a set of signal validity tests to separate the signals into clean and dirty groups. In the second step, we train an initial model on the clean signals and then reweigting the dirty signals based on the residual error. A final model is retrained on both the clean signals and the reweighted dirty signals. In the theoretical analysis, we prove that the proposed three-step approach is able to tolerate much higher noise level than the vanilla robust regression methods if two reweighting rules are followed. We validate the superiority of the proposed method in our real-time high precision positioning system against several popular state-of-the-art robust regression methods. Our method achieves centimeter positioning accuracy in the benchmark region with probability $78.4\%$ , outperforming the second best baseline method by a margin of $8.3\%$. The benchmark takes 6 hours on 20,000 CPU cores or 14 years on a single CPU.

Which Factorization Machine Modeling is Better: A Theoretical Answer with Optimal Guarantee

Factorization machine (FM) is a popular machine learning model to capture the second order feature interactions. The optimal learning guarantee of FM and its generalized version is not yet developed. For a rank $k$ generalized FM of $d$ dimensional input, the previous best known sampling complexity is $\mathcal{O}[k^{3}d\cdot\mathrm{polylog}(kd)]$ under Gaussian distribution. This bound is sub-optimal comparing to the information theoretical lower bound $\mathcal{O}(kd)$. In this work, we aim to tighten this bound towards optimal and generalize the analysis to sub-gaussian distribution. We prove that when the input data satisfies the so-called $\tau$-Moment Invertible Property, the sampling complexity of generalized FM can be improved to $\mathcal{O}[k^{2}d\cdot\mathrm{polylog}(kd)/\tau^{2}]$. When the second order self-interaction terms are excluded in the generalized FM, the bound can be improved to the optimal $\mathcal{O}[kd\cdot\mathrm{polylog}(kd)]$ up to the logarithmic factors. Our analysis also suggests that the positive semi-definite constraint in the conventional FM is redundant as it does not improve the sampling complexity while making the model difficult to optimize. We evaluate our improved FM model in real-time high precision GPS signal calibration task to validate its superiority.

RobustSTL: A Robust Seasonal-Trend Decomposition Algorithm for Long Time Series

Decomposing complex time series into trend, seasonality, and remainder components is an important task to facilitate time series anomaly detection and forecasting. Although numerous methods have been proposed, there are still many time series characteristics exhibiting in real-world data which are not addressed properly, including 1) ability to handle seasonality fluctuation and shift, and abrupt change in trend and reminder; 2) robustness on data with anomalies; 3) applicability on time series with long seasonality period. In the paper, we propose a novel and generic time series decomposition algorithm to address these challenges. Specifically, we extract the trend component robustly by solving a regression problem using the least absolute deviations loss with sparse regularization. Based on the extracted trend, we apply the the non-local seasonal filtering to extract the seasonality component. This process is repeated until accurate decomposition is obtained. Experiments on different synthetic and real-world time series datasets demonstrate that our method outperforms existing solutions.

Parallel Restarted SGD for Non-Convex Optimization with Faster Convergence and Less Communication

For large scale non-convex stochastic optimization, parallel mini-batch SGD using multiple workers ideally can achieve a linear speed-up with respect to the number of workers compared with SGD over a single worker. However, such linear scalability in practice is significantly limited by the growing demand for communication as more workers are involved. This is because the classical parallel mini-batch SGD requires gradient or model exchanges between workers (possibly through an intermediate server) at every iteration. In this paper, we study whether it is possible to maintain the linear speed-up property of parallel mini-batch SGD by using less frequent message passing between workers. We consider the parallel restarted SGD method where each worker periodically restarts its SGD by using the node average as a new initial point. Such a strategy invokes inter-node communication only when computing the node average to restart local SGD but otherwise is fully parallel with no communication overhead. We prove that the parallel restarted SGD method can maintain the same convergence rate as the classical parallel mini-batch SGD while reducing the communication overhead by a factor of $O(T^{1/4})$. The parallel restarted SGD strategy was previously used as a common practice, known as model averaging, for training deep neural networks. Earlier empirical works have observed that model averaging can achieve an almost linear speed-up if the averaging interval is carefully controlled. The results in this paper can serve as theoretical justifications for these empirical results on model averaging and provide practical guidelines for applying model averaging.

Large-scale Distance Metric Learning with Uncertainty

Distance metric learning (DML) has been studied extensively in the past decades for its superior performance with distance-based algorithms. Most of the existing methods propose to learn a distance metric with pairwise or triplet constraints. However, the number of constraints is quadratic or even cubic in the number of the original examples, which makes it challenging for DML to handle the large-scale data set. Besides, the real-world data may contain various uncertainty, especially for the image data. The uncertainty can mislead the learning procedure and cause the performance degradation. By investigating the image data, we find that the original data can be observed from a small set of clean latent examples with different distortions. In this work, we propose the margin preserving metric learning framework to learn the distance metric and latent examples simultaneously. By leveraging the ideal properties of latent examples, the training efficiency can be improved significantly while the learned metric also becomes robust to the uncertainty in the original data. Furthermore, we can show that the metric is learned from latent examples only, but it can preserve the large margin property even for the original data. The empirical study on the benchmark image data sets demonstrates the efficacy and efficiency of the proposed method.

Learning with Non-Convex Truncated Losses by SGD

Learning with a {\it convex loss} function has been a dominating paradigm for many years. It remains an interesting question how non-convex loss functions help improve the generalization of learning with broad applicability. In this paper, we study a family of objective functions formed by truncating traditional loss functions, which is applicable to both shallow learning and deep learning. Truncating loss functions has potential to be less vulnerable and more robust to large noise in observations that could be adversarial. More importantly, it is a generic technique without assuming the knowledge of noise distribution. To justify non-convex learning with truncated losses, we establish excess risk bounds of empirical risk minimization based on truncated losses for heavy-tailed output, and statistical error of an approximate stationary point found by stochastic gradient descent (SGD) method. Our experiments for shallow and deep learning for regression with outliers, corrupted data and heavy-tailed noise further justify the proposed method.

Robust Optimization over Multiple Domains

Recently, machine learning becomes important for the cloud computing service. Users of cloud computing can benefit from the sophisticated machine learning models provided by the service. Considering that users can come from different domains with the same problem, an ideal model has to be applicable over multiple domains. In this work, we propose to address this challenge by developing a framework of robust optimization. In lieu of minimizing the empirical risk, we aim to learn a model optimized with an adversarial distribution over multiple domains. Besides the convex model, we analyze the convergence rate of learning a robust non-convex model due to its dominating performance on many real-word applications. Furthermore, we demonstrate that both the robustness of the framework and the convergence rate can be enhanced by introducing appropriate regularizers for the adversarial distribution. The empirical study on real-world fine-grained visual categorization and digits recognition tasks verifies the effectiveness and efficiency of the proposed framework.

Multinomial Logit Bandit with Linear Utility Functions

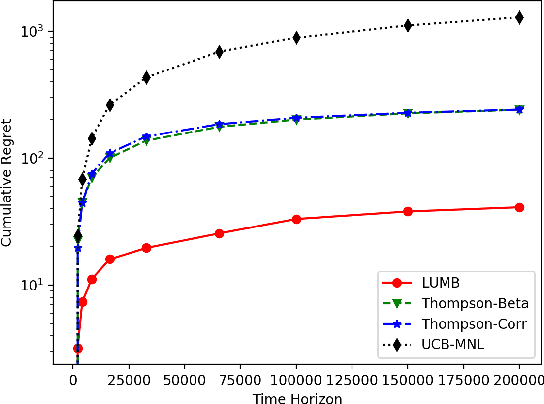
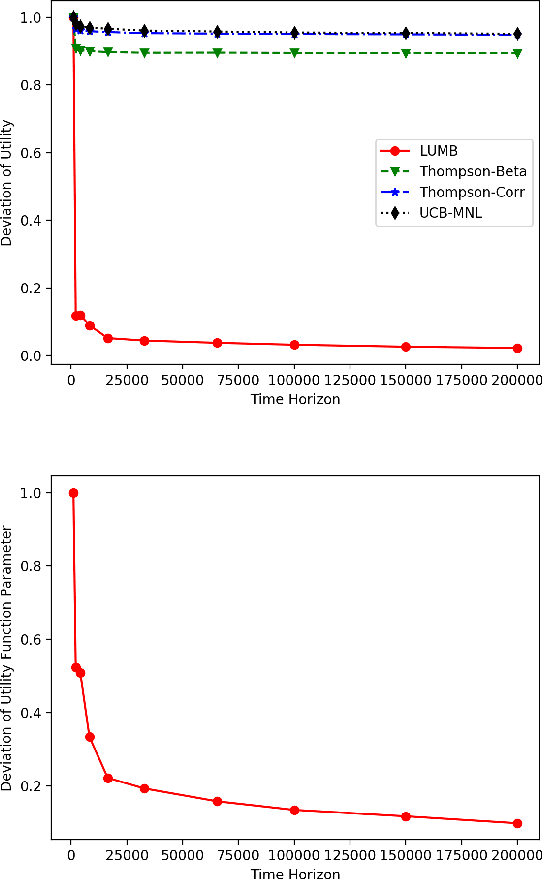
Multinomial logit bandit is a sequential subset selection problem which arises in many applications. In each round, the player selects a $K$-cardinality subset from $N$ candidate items, and receives a reward which is governed by a {\it multinomial logit} (MNL) choice model considering both item utility and substitution property among items. The player's objective is to dynamically learn the parameters of MNL model and maximize cumulative reward over a finite horizon $T$. This problem faces the exploration-exploitation dilemma, and the involved combinatorial nature makes it non-trivial. In recent years, there have developed some algorithms by exploiting specific characteristics of the MNL model, but all of them estimate the parameters of MNL model separately and incur a regret no better than $\tilde{O}\big(\sqrt{NT}\big)$ which is not preferred for large candidate set size $N$. In this paper, we consider the {\it linear utility} MNL choice model whose item utilities are represented as linear functions of $d$-dimension item features, and propose an algorithm, titled {\bf LUMB}, to exploit the underlying structure. It is proven that the proposed algorithm achieves $\tilde{O}\big(dK\sqrt{T}\big)$ regret which is free of candidate set size. Experiments show the superiority of the proposed algorithm.

Extremely Low Bit Neural Network: Squeeze the Last Bit Out with ADMM

Although deep learning models are highly effective for various learning tasks, their high computational costs prohibit the deployment to scenarios where either memory or computational resources are limited. In this paper, we focus on compressing and accelerating deep models with network weights represented by very small numbers of bits, referred to as extremely low bit neural network. We model this problem as a discretely constrained optimization problem. Borrowing the idea from Alternating Direction Method of Multipliers (ADMM), we decouple the continuous parameters from the discrete constraints of network, and cast the original hard problem into several subproblems. We propose to solve these subproblems using extragradient and iterative quantization algorithms that lead to considerably faster convergency compared to conventional optimization methods. Extensive experiments on image recognition and object detection verify that the proposed algorithm is more effective than state-of-the-art approaches when coming to extremely low bit neural network.

Similarity Learning via Adaptive Regression and Its Application to Image Retrieval

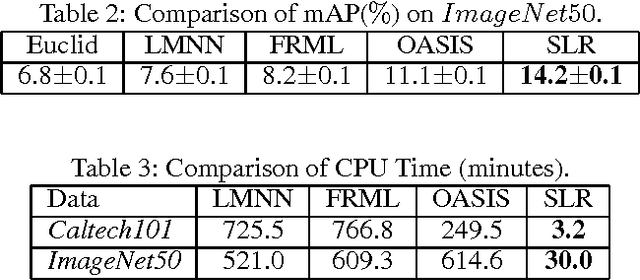
We study the problem of similarity learning and its application to image retrieval with large-scale data. The similarity between pairs of images can be measured by the distances between their high dimensional representations, and the problem of learning the appropriate similarity is often addressed by distance metric learning. However, distance metric learning requires the learned metric to be a PSD matrix, which is computational expensive and not necessary for retrieval ranking problem. On the other hand, the bilinear model is shown to be more flexible for large-scale image retrieval task, hence, we adopt it to learn a matrix for estimating pairwise similarities under the regression framework. By adaptively updating the target matrix in regression, we can mimic the hinge loss, which is more appropriate for similarity learning problem. Although the regression problem can have the closed-form solution, the computational cost can be very expensive. The computational challenges come from two aspects: the number of images can be very large and image features have high dimensionality. We address the first challenge by compressing the data by a randomized algorithm with the theoretical guarantee. For the high dimensional issue, we address it by taking low rank assumption and applying alternating method to obtain the partial matrix, which has a global optimal solution. Empirical studies on real world image datasets (i.e., Caltech and ImageNet) demonstrate the effectiveness and efficiency of the proposed method.