Similarity Learning via Adaptive Regression and Its Application to Image Retrieval
Paper and Code
Dec 06, 2015

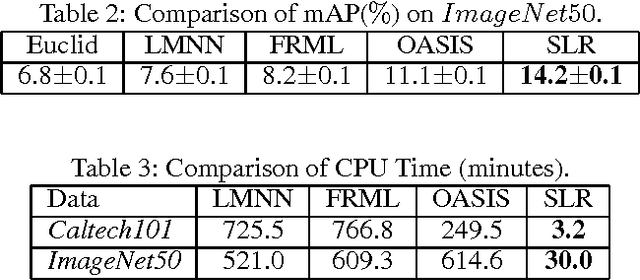

We study the problem of similarity learning and its application to image retrieval with large-scale data. The similarity between pairs of images can be measured by the distances between their high dimensional representations, and the problem of learning the appropriate similarity is often addressed by distance metric learning. However, distance metric learning requires the learned metric to be a PSD matrix, which is computational expensive and not necessary for retrieval ranking problem. On the other hand, the bilinear model is shown to be more flexible for large-scale image retrieval task, hence, we adopt it to learn a matrix for estimating pairwise similarities under the regression framework. By adaptively updating the target matrix in regression, we can mimic the hinge loss, which is more appropriate for similarity learning problem. Although the regression problem can have the closed-form solution, the computational cost can be very expensive. The computational challenges come from two aspects: the number of images can be very large and image features have high dimensionality. We address the first challenge by compressing the data by a randomized algorithm with the theoretical guarantee. For the high dimensional issue, we address it by taking low rank assumption and applying alternating method to obtain the partial matrix, which has a global optimal solution. Empirical studies on real world image datasets (i.e., Caltech and ImageNet) demonstrate the effectiveness and efficiency of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge