Xiaomin Song
Deep Reversible Consistency Learning for Cross-modal Retrieval
Jan 10, 2025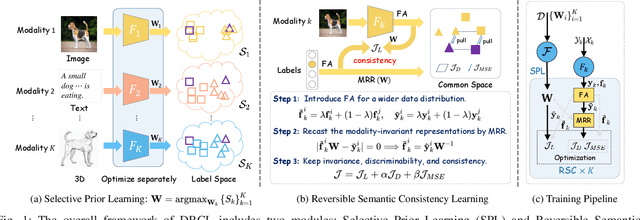
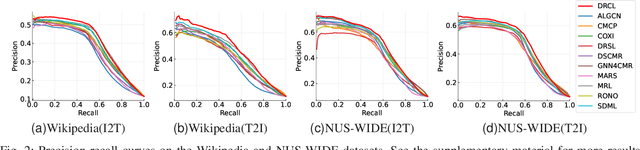
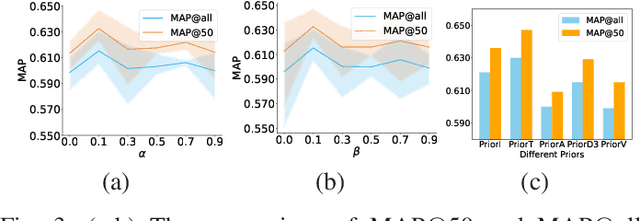
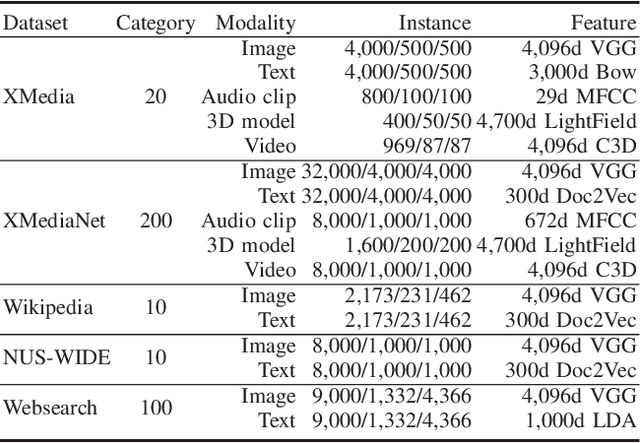
Abstract:Cross-modal retrieval (CMR) typically involves learning common representations to directly measure similarities between multimodal samples. Most existing CMR methods commonly assume multimodal samples in pairs and employ joint training to learn common representations, limiting the flexibility of CMR. Although some methods adopt independent training strategies for each modality to improve flexibility in CMR, they utilize the randomly initialized orthogonal matrices to guide representation learning, which is suboptimal since they assume inter-class samples are independent of each other, limiting the potential of semantic alignments between sample representations and ground-truth labels. To address these issues, we propose a novel method termed Deep Reversible Consistency Learning (DRCL) for cross-modal retrieval. DRCL includes two core modules, \ie Selective Prior Learning (SPL) and Reversible Semantic Consistency learning (RSC). More specifically, SPL first learns a transformation weight matrix on each modality and selects the best one based on the quality score as the Prior, which greatly avoids blind selection of priors learned from low-quality modalities. Then, RSC employs a Modality-invariant Representation Recasting mechanism (MRR) to recast the potential modality-invariant representations from sample semantic labels by the generalized inverse matrix of the prior. Since labels are devoid of modal-specific information, we utilize the recast features to guide the representation learning, thus maintaining semantic consistency to the fullest extent possible. In addition, a feature augmentation mechanism (FA) is introduced in RSC to encourage the model to learn over a wider data distribution for diversity. Finally, extensive experiments conducted on five widely used datasets and comparisons with 15 state-of-the-art baselines demonstrate the effectiveness and superiority of our DRCL.
Robust Self-Paced Hashing for Cross-Modal Retrieval with Noisy Labels
Jan 03, 2025



Abstract:Cross-modal hashing (CMH) has appeared as a popular technique for cross-modal retrieval due to its low storage cost and high computational efficiency in large-scale data. Most existing methods implicitly assume that multi-modal data is correctly labeled, which is expensive and even unattainable due to the inevitable imperfect annotations (i.e., noisy labels) in real-world scenarios. Inspired by human cognitive learning, a few methods introduce self-paced learning (SPL) to gradually train the model from easy to hard samples, which is often used to mitigate the effects of feature noise or outliers. It is a less-touched problem that how to utilize SPL to alleviate the misleading of noisy labels on the hash model. To tackle this problem, we propose a new cognitive cross-modal retrieval method called Robust Self-paced Hashing with Noisy Labels (RSHNL), which can mimic the human cognitive process to identify the noise while embracing robustness against noisy labels. Specifically, we first propose a contrastive hashing learning (CHL) scheme to improve multi-modal consistency, thereby reducing the inherent semantic gap. Afterward, we propose center aggregation learning (CAL) to mitigate the intra-class variations. Finally, we propose Noise-tolerance Self-paced Hashing (NSH) that dynamically estimates the learning difficulty for each instance and distinguishes noisy labels through the difficulty level. For all estimated clean pairs, we further adopt a self-paced regularizer to gradually learn hash codes from easy to hard. Extensive experiments demonstrate that the proposed RSHNL performs remarkably well over the state-of-the-art CMH methods.
Robust Time Series Dissimilarity Measure for Outlier Detection and Periodicity Detection
Jun 07, 2022



Abstract:Dynamic time warping (DTW) is an effective dissimilarity measure in many time series applications. Despite its popularity, it is prone to noises and outliers, which leads to singularity problem and bias in the measurement. The time complexity of DTW is quadratic to the length of time series, making it inapplicable in real-time applications. In this paper, we propose a novel time series dissimilarity measure named RobustDTW to reduce the effects of noises and outliers. Specifically, the RobustDTW estimates the trend and optimizes the time warp in an alternating manner by utilizing our designed temporal graph trend filtering. To improve efficiency, we propose a multi-level framework that estimates the trend and the warp function at a lower resolution, and then repeatedly refines them at a higher resolution. Based on the proposed RobustDTW, we further extend it to periodicity detection and outlier time series detection. Experiments on real-world datasets demonstrate the superior performance of RobustDTW compared to DTW variants in both outlier time series detection and periodicity detection.
Time Series Data Augmentation for Deep Learning: A Survey
Feb 27, 2020



Abstract:Deep learning performs remarkably well on many time series analysis tasks recently. The superior performance of deep neural networks relies heavily on a large number of training data to avoid overfitting. However, the labeled data of many real-world time series applications may be limited such as classification in medical time series and anomaly detection in AIOps. As an effective way to enhance the size and quality of the training data, data augmentation is crucial to the successful application of deep learning models on time series data. In this paper, we systematically review different data augmentation methods for time series. We propose a taxonomy for the reviewed methods, and then provide a structured review for these methods by highlighting their strengths and limitations. We also empirically compare different data augmentation methods for different tasks including time series anomaly detection, classification and forecasting. Finally, we discuss and highlight future research directions, including data augmentation in time-frequency domain, augmentation combination, and data augmentation and weighting for imbalanced class.
RobustTAD: Robust Time Series Anomaly Detection via Decomposition and Convolutional Neural Networks
Feb 21, 2020



Abstract:The monitoring and management of numerous and diverse time series data at Alibaba Group calls for an effective and scalable time series anomaly detection service. In this paper, we propose RobustTAD, a Robust Time series Anomaly Detection framework by integrating robust seasonal-trend decomposition and convolutional neural network for time series data. The seasonal-trend decomposition can effectively handle complicated patterns in time series, and meanwhile significantly simplifies the architecture of the neural network, which is an encoder-decoder architecture with skip connections. This architecture can effectively capture the multi-scale information from time series, which is very useful in anomaly detection. Due to the limited labeled data in time series anomaly detection, we systematically investigate data augmentation methods in both time and frequency domains. We also introduce label-based weight and value-based weight in the loss function by utilizing the unbalanced nature of the time series anomaly detection problem. Compared with the widely used forecasting-based anomaly detection algorithms, decomposition-based algorithms, traditional statistical algorithms, as well as recent neural network based algorithms, RobustTAD performs significantly better on public benchmark datasets. It is deployed as a public online service and widely adopted in different business scenarios at Alibaba Group.
RobustTrend: A Huber Loss with a Combined First and Second Order Difference Regularization for Time Series Trend Filtering
Jun 27, 2019



Abstract:Extracting the underlying trend signal is a crucial step to facilitate time series analysis like forecasting and anomaly detection. Besides noise signal, time series can contain not only outliers but also abrupt trend changes in real-world scenarios. To deal with these challenges, we propose a robust trend filtering algorithm based on robust statistics and sparse learning. Specifically, we adopt the Huber loss to suppress outliers, and utilize a combination of the first order and second order difference on the trend component as regularization to capture both slow and abrupt trend changes. Furthermore, an efficient method is designed to solve the proposed robust trend filtering based on majorization minimization (MM) and alternative direction method of multipliers (ADMM). We compared our proposed robust trend filter with other nine state-of-the-art trend filtering algorithms on both synthetic and real-world datasets. The experiments demonstrate that our algorithm outperforms existing methods.
Robust Gaussian Process Regression for Real-Time High Precision GPS Signal Enhancement
Jun 03, 2019


Abstract:Satellite-based positioning system such as GPS often suffers from large amount of noise that degrades the positioning accuracy dramatically especially in real-time applications. In this work, we consider a data-mining approach to enhance the GPS signal. We build a large-scale high precision GPS receiver grid system to collect real-time GPS signals for training. The Gaussian Process (GP) regression is chosen to model the vertical Total Electron Content (vTEC) distribution of the ionosphere of the Earth. Our experiments show that the noise in the real-time GPS signals often exceeds the breakdown point of the conventional robust regression methods resulting in sub-optimal system performance. We propose a three-step approach to address this challenge. In the first step we perform a set of signal validity tests to separate the signals into clean and dirty groups. In the second step, we train an initial model on the clean signals and then reweigting the dirty signals based on the residual error. A final model is retrained on both the clean signals and the reweighted dirty signals. In the theoretical analysis, we prove that the proposed three-step approach is able to tolerate much higher noise level than the vanilla robust regression methods if two reweighting rules are followed. We validate the superiority of the proposed method in our real-time high precision positioning system against several popular state-of-the-art robust regression methods. Our method achieves centimeter positioning accuracy in the benchmark region with probability $78.4\%$ , outperforming the second best baseline method by a margin of $8.3\%$. The benchmark takes 6 hours on 20,000 CPU cores or 14 years on a single CPU.
Which Factorization Machine Modeling is Better: A Theoretical Answer with Optimal Guarantee
Jan 30, 2019

Abstract:Factorization machine (FM) is a popular machine learning model to capture the second order feature interactions. The optimal learning guarantee of FM and its generalized version is not yet developed. For a rank $k$ generalized FM of $d$ dimensional input, the previous best known sampling complexity is $\mathcal{O}[k^{3}d\cdot\mathrm{polylog}(kd)]$ under Gaussian distribution. This bound is sub-optimal comparing to the information theoretical lower bound $\mathcal{O}(kd)$. In this work, we aim to tighten this bound towards optimal and generalize the analysis to sub-gaussian distribution. We prove that when the input data satisfies the so-called $\tau$-Moment Invertible Property, the sampling complexity of generalized FM can be improved to $\mathcal{O}[k^{2}d\cdot\mathrm{polylog}(kd)/\tau^{2}]$. When the second order self-interaction terms are excluded in the generalized FM, the bound can be improved to the optimal $\mathcal{O}[kd\cdot\mathrm{polylog}(kd)]$ up to the logarithmic factors. Our analysis also suggests that the positive semi-definite constraint in the conventional FM is redundant as it does not improve the sampling complexity while making the model difficult to optimize. We evaluate our improved FM model in real-time high precision GPS signal calibration task to validate its superiority.
RobustSTL: A Robust Seasonal-Trend Decomposition Algorithm for Long Time Series
Dec 05, 2018



Abstract:Decomposing complex time series into trend, seasonality, and remainder components is an important task to facilitate time series anomaly detection and forecasting. Although numerous methods have been proposed, there are still many time series characteristics exhibiting in real-world data which are not addressed properly, including 1) ability to handle seasonality fluctuation and shift, and abrupt change in trend and reminder; 2) robustness on data with anomalies; 3) applicability on time series with long seasonality period. In the paper, we propose a novel and generic time series decomposition algorithm to address these challenges. Specifically, we extract the trend component robustly by solving a regression problem using the least absolute deviations loss with sparse regularization. Based on the extracted trend, we apply the the non-local seasonal filtering to extract the seasonality component. This process is repeated until accurate decomposition is obtained. Experiments on different synthetic and real-world time series datasets demonstrate that our method outperforms existing solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge