Multinomial Logit Bandit with Linear Utility Functions
Paper and Code
May 08, 2018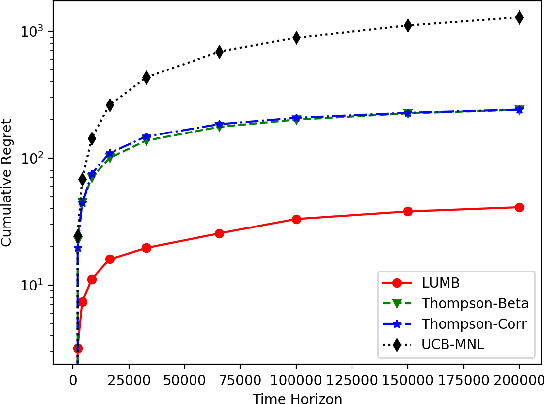
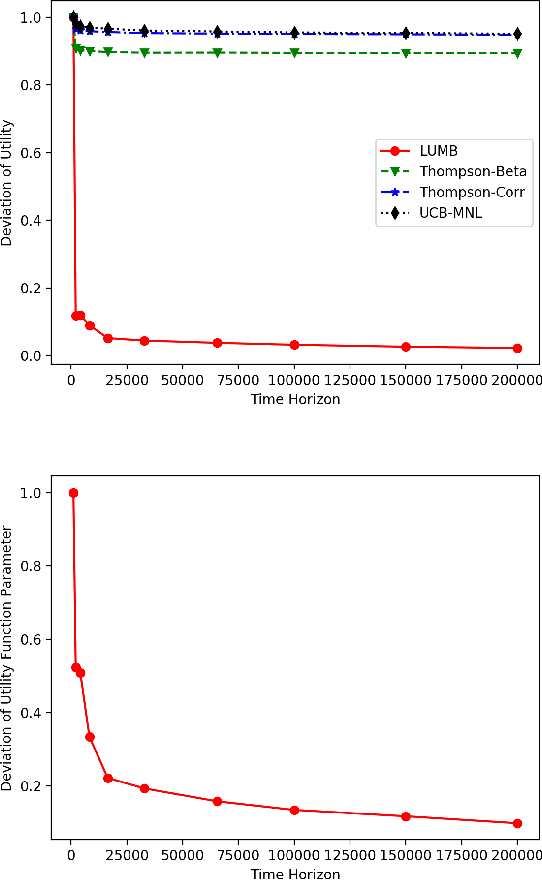
Multinomial logit bandit is a sequential subset selection problem which arises in many applications. In each round, the player selects a $K$-cardinality subset from $N$ candidate items, and receives a reward which is governed by a {\it multinomial logit} (MNL) choice model considering both item utility and substitution property among items. The player's objective is to dynamically learn the parameters of MNL model and maximize cumulative reward over a finite horizon $T$. This problem faces the exploration-exploitation dilemma, and the involved combinatorial nature makes it non-trivial. In recent years, there have developed some algorithms by exploiting specific characteristics of the MNL model, but all of them estimate the parameters of MNL model separately and incur a regret no better than $\tilde{O}\big(\sqrt{NT}\big)$ which is not preferred for large candidate set size $N$. In this paper, we consider the {\it linear utility} MNL choice model whose item utilities are represented as linear functions of $d$-dimension item features, and propose an algorithm, titled {\bf LUMB}, to exploit the underlying structure. It is proven that the proposed algorithm achieves $\tilde{O}\big(dK\sqrt{T}\big)$ regret which is free of candidate set size. Experiments show the superiority of the proposed algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge