Unsigned Orthogonal Distance Fields: An Accurate Neural Implicit Representation for Diverse 3D Shapes

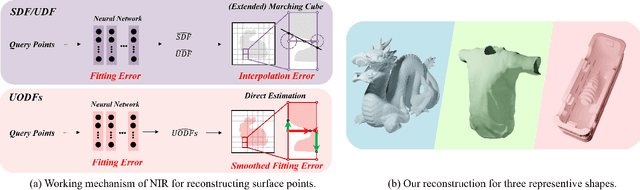
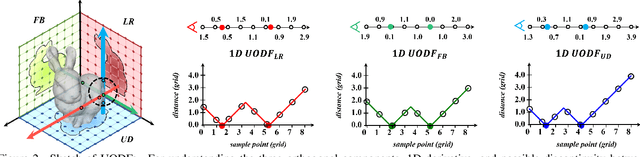
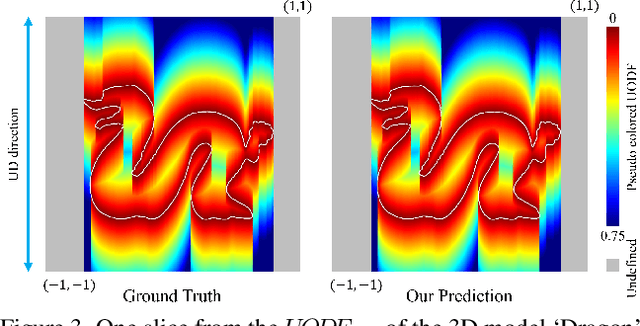
Neural implicit representation of geometric shapes has witnessed considerable advancements in recent years. However, common distance field based implicit representations, specifically signed distance field (SDF) for watertight shapes or unsigned distance field (UDF) for arbitrary shapes, routinely suffer from degradation of reconstruction accuracy when converting to explicit surface points and meshes. In this paper, we introduce a novel neural implicit representation based on unsigned orthogonal distance fields (UODFs). In UODFs, the minimal unsigned distance from any spatial point to the shape surface is defined solely in one orthogonal direction, contrasting with the multi-directional determination made by SDF and UDF. Consequently, every point in the 3D UODFs can directly access its closest surface points along three orthogonal directions. This distinctive feature leverages the accurate reconstruction of surface points without interpolation errors. We verify the effectiveness of UODFs through a range of reconstruction examples, extending from simple watertight or non-watertight shapes to complex shapes that include hollows, internal or assembling structures.

Fast and Interpretable 2D Homography Decomposition: Similarity-Kernel-Similarity and Affine-Core-Affine Transformations

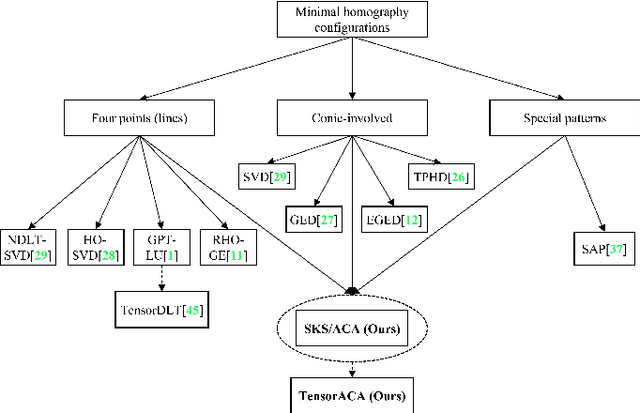
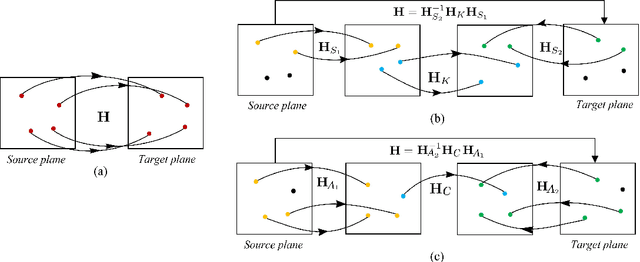
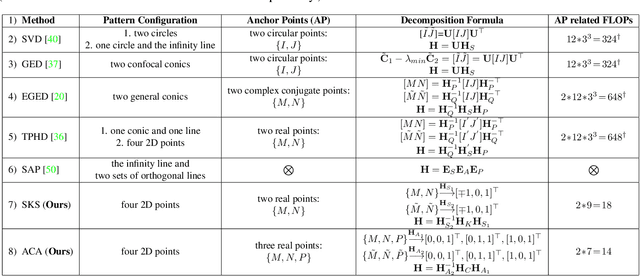
In this paper, we present two fast and interpretable decomposition methods for 2D homography, which are named Similarity-Kernel-Similarity (SKS) and Affine-Core-Affine (ACA) transformations respectively. Under the minimal $4$-point configuration, the first and the last similarity transformations in SKS are computed by two anchor points on target and source planes, respectively. Then, the other two point correspondences can be exploited to compute the middle kernel transformation with only four parameters. Furthermore, ACA uses three anchor points to compute the first and the last affine transformations, followed by computation of the middle core transformation utilizing the other one point correspondence. ACA can compute a homography up to a scale with only $85$ floating-point operations (FLOPs), without even any division operations. Therefore, as a plug-in module, ACA facilitates the traditional feature-based Random Sample Consensus (RANSAC) pipeline, as well as deep homography pipelines estimating $4$-point offsets. In addition to the advantages of geometric parameterization and computational efficiency, SKS and ACA can express each element of homography by a polynomial of input coordinates ($7$th degree to $9$th degree), extend the existing essential Similarity-Affine-Projective (SAP) decomposition and calculate 2D affine transformations in a unified way. Source codes are released in https://github.com/cscvlab/SKS-Homography.

An Efficient End-to-End 3D Model Reconstruction based on Neural Architecture Search

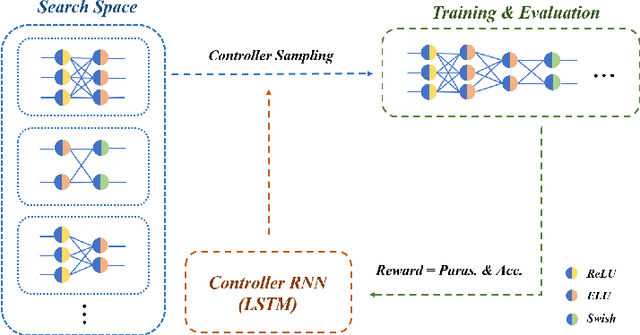
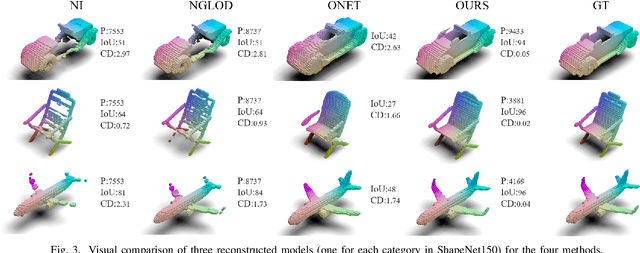
Using neural networks to represent 3D objects has become popular. However, many previous works employ neural networks with fixed architecture and size to represent different 3D objects, which lead to excessive network parameters for simple objects and limited reconstruction accuracy for complex objects. For each 3D model, it is desirable to have an end-to-end neural network with as few parameters as possible to achieve high-fidelity reconstruction. In this paper, we propose an efficient model reconstruction method utilizing neural architecture search (NAS) and binary classification. Taking the number of layers, the number of nodes in each layer, and the activation function of each layer as the search space, a specific network architecture can be obtained based on reinforcement learning technology. Furthermore, to get rid of the traditional surface reconstruction algorithms (e.g., marching cube) used after network inference, we complete the end-to-end network by classifying binary voxels. Compared to other signed distance field (SDF) prediction or binary classification networks, our method achieves significantly higher reconstruction accuracy using fewer network parameters.

High-fidelity 3D Model Compression based on Key Spheres

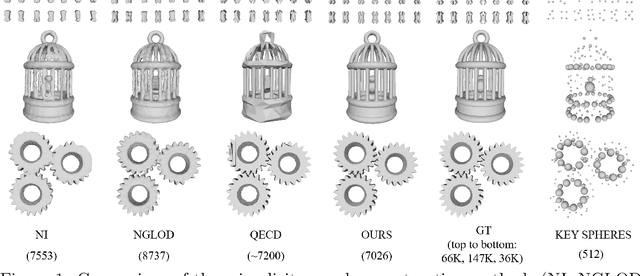
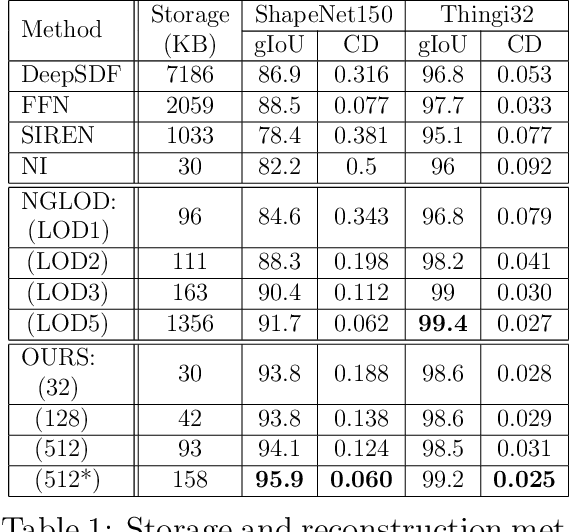
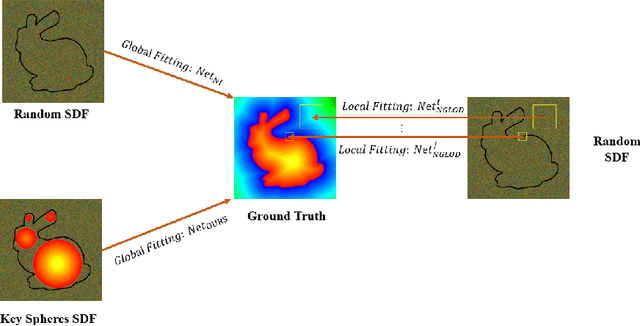
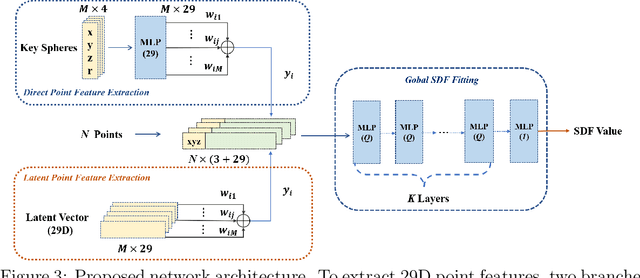
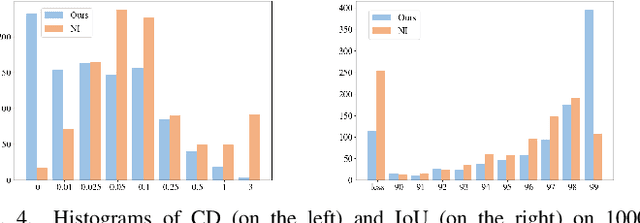
In recent years, neural signed distance function (SDF) has become one of the most effective representation methods for 3D models. By learning continuous SDFs in 3D space, neural networks can predict the distance from a given query space point to its closest object surface,whose positive and negative signs denote inside and outside of the object, respectively. Training a specific network for each 3D model, which individually embeds its shape, can realize compressed representation of objects by storing fewer network (and possibly latent) parameters. Consequently, reconstruction through network inference and surface recovery can be achieved. In this paper, we propose an SDF prediction network using explicit key spheres as input. Key spheres are extracted from the internal space of objects, whose centers either have relatively larger SDF values (sphere radii), or are located at essential positions. By inputting the spatial information of multiple spheres which imply different local shapes, the proposed method can significantly improve the reconstruction accuracy with a negligible storage cost. Compared to previous works, our method achieves the high-fidelity and high-compression 3D object coding and reconstruction. Experiments conducted on three datasets verify the superior performance of our method.

SN-Graph: a Minimalist 3D Object Representation for Classification

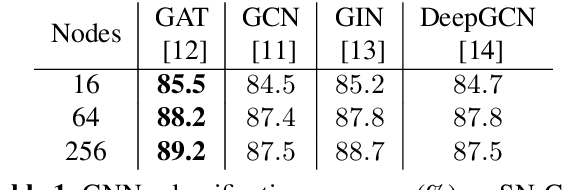
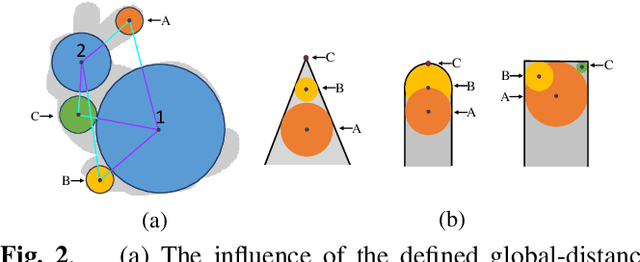
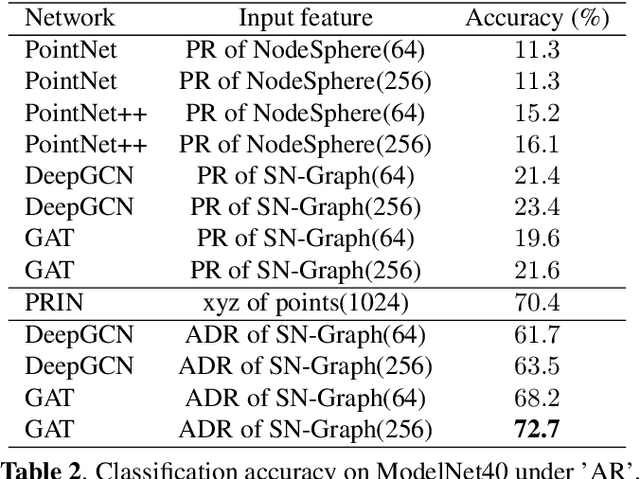
Using deep learning techniques to process 3D objects has achieved many successes. However, few methods focus on the representation of 3D objects, which could be more effective for specific tasks than traditional representations, such as point clouds, voxels, and multi-view images. In this paper, we propose a Sphere Node Graph (SN-Graph) to represent 3D objects. Specifically, we extract a certain number of internal spheres (as nodes) from the signed distance field (SDF), and then establish connections (as edges) among the sphere nodes to construct a graph, which is seamlessly suitable for 3D analysis using graph neural network (GNN). Experiments conducted on the ModelNet40 dataset show that when there are fewer nodes in the graph or the tested objects are rotated arbitrarily, the classification accuracy of SN-Graph is significantly higher than the state-of-the-art methods.

Spherical Transformer: Adapting Spherical Signal to CNNs

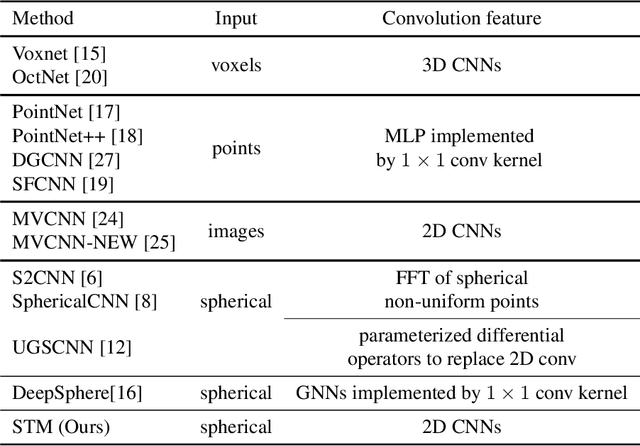
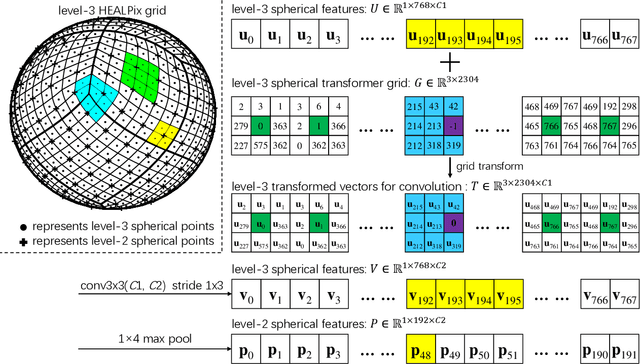
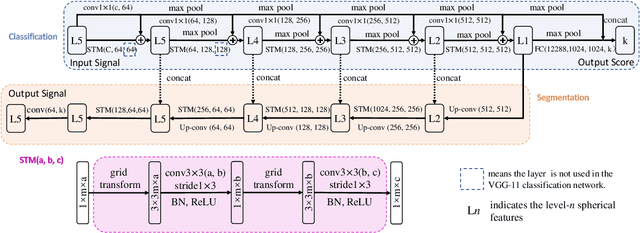
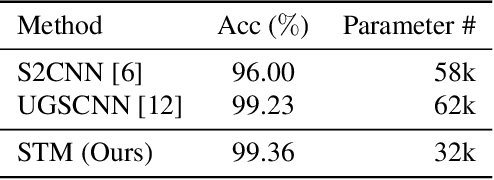
Convolutional neural networks (CNNs) have been widely used in various vision tasks, e.g. image classification, semantic segmentation, etc. Unfortunately, standard 2D CNNs are not well suited for spherical signals such as panorama images or spherical projections, as the sphere is an unstructured grid. In this paper, we present Spherical Transformer which can transform spherical signals into vectors that can be directly processed by standard CNNs such that many well-designed CNNs architectures can be reused across tasks and datasets by pretraining. To this end, the proposed method first uses locally structured sampling methods such as HEALPix to construct a transformer grid by using the information of spherical points and its adjacent points, and then transforms the spherical signals to the vectors through the grid. By building the Spherical Transformer module, we can use multiple CNN architectures directly. We evaluate our approach on the tasks of spherical MNIST recognition, 3D object classification and omnidirectional image semantic segmentation. For 3D object classification, we further propose a rendering-based projection method to improve the performance and a rotational-equivariant model to improve the anti-rotation ability. Experimental results on three tasks show that our approach achieves superior performance over state-of-the-art methods.

Fast Hybrid Cascade for Voxel-based 3D Object Classification

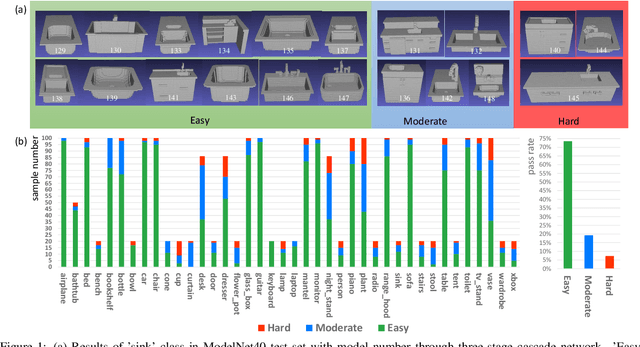
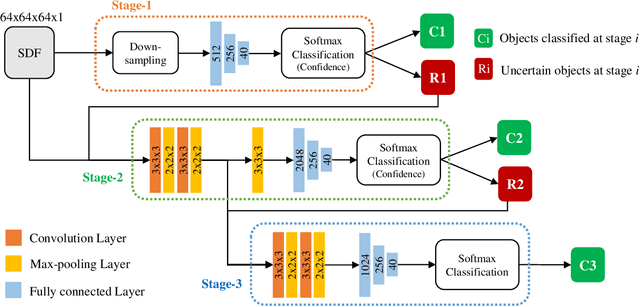
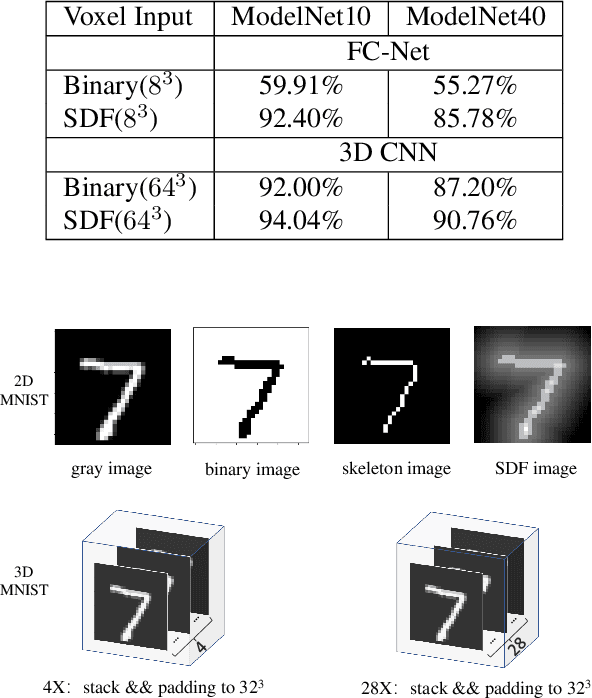
Voxel-based 3D object classification has been frequently studied in recent years. The previous methods often directly convert the classic 2D convolution into a 3D form applied to an object with binary voxel representation. In this paper, we investigate the reason why binary voxel representation is not very suitable for 3D convolution and how to simultaneously improve the performance both in accuracy and speed. We show that by giving each voxel a signed distance value, the accuracy will gain about 30% promotion compared with binary voxel representation using a two-layer fully connected network. We then propose a fast fully connected and convolution hybrid cascade network for voxel-based 3D object classification. This threestage cascade network can divide 3D models into three categories: easy, moderate and hard. Consequently, the mean inference time (0.3ms) can speedup about 5x and 2x compared with the state-of-the-art point cloud and voxel based methods respectively, while achieving the highest accuracy in the latter category of methods (92%). Experiments with ModelNet andMNIST verify the performance of the proposed hybrid cascade network.

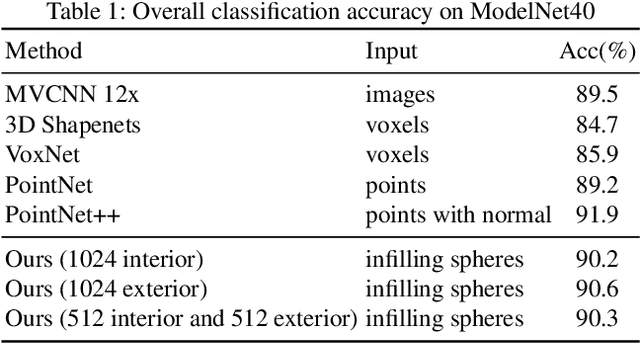
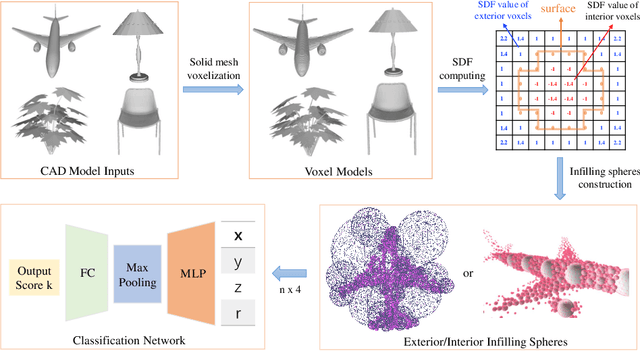
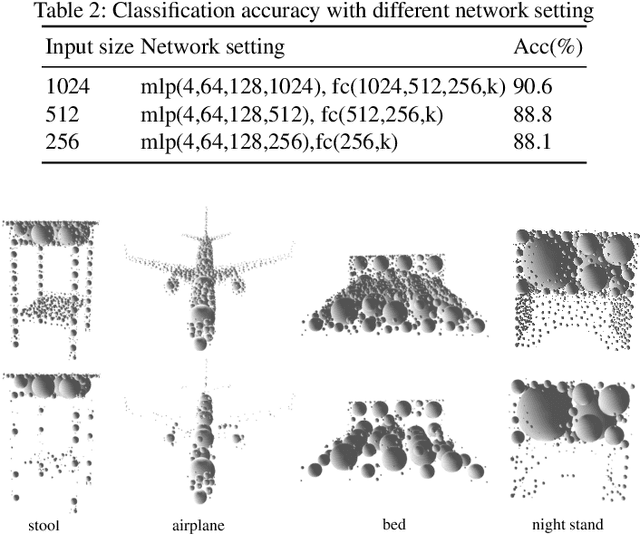
InSphereNet: a Concise Representation and Classification Method for 3D Object

In this paper, we present an InSphereNet method for the problem of 3D object classification. Unlike previous methods that use points, voxels, or multi-view images as inputs of deep neural network (DNN), the proposed method constructs a class of more representative features named infilling spheres from signed distance field (SDF). Because of the admirable spatial representation of infilling spheres, we can not only utilize very fewer number of spheres to accomplish classification task, but also design a lightweight InSphereNet with less layers and parameters than previous methods. Experiments on ModelNet40 show that the proposed method leads to superior performance than PointNet and PointNet++ in accuracy. In particular, if there are only a few dozen sphere inputs or about 100000 DNN parameters, the accuracy of our method remains at a very high level (over 88%). This further validates the conciseness and effectiveness of the proposed InSphere 3D representation. Keywords: 3D object classification , signed distance field , deep learning , infilling sphere