Decoupled Geometric Parameterization and its Application in Deep Homography Estimation

Planar homography, with eight degrees of freedom (DOFs), is fundamental in numerous computer vision tasks. While the positional offsets of four corners are widely adopted (especially in neural network predictions), this parameterization lacks geometric interpretability and typically requires solving a linear system to compute the homography matrix. This paper presents a novel geometric parameterization of homographies, leveraging the similarity-kernel-similarity (SKS) decomposition for projective transformations. Two independent sets of four geometric parameters are decoupled: one for a similarity transformation and the other for the kernel transformation. Additionally, the geometric interpretation linearly relating the four kernel transformation parameters to angular offsets is derived. Our proposed parameterization allows for direct homography estimation through matrix multiplication, eliminating the need for solving a linear system, and achieves performance comparable to the four-corner positional offsets in deep homography estimation.

Are Minimal Radial Distortion Solvers Really Necessary for Relative Pose Estimation?

Estimating the relative pose between two cameras is a fundamental step in many applications such as Structure-from-Motion. The common approach to relative pose estimation is to apply a minimal solver inside a RANSAC loop. Highly efficient solvers exist for pinhole cameras. Yet, (nearly) all cameras exhibit radial distortion. Not modeling radial distortion leads to (significantly) worse results. However, minimal radial distortion solvers are significantly more complex than pinhole solvers, both in terms of run-time and implementation efforts. This paper compares radial distortion solvers with two simple-to-implement approaches that do not use minimal radial distortion solvers: The first approach combines an efficient pinhole solver with sampled radial undistortion parameters, where the sampled parameters are used for undistortion prior to applying the pinhole solver. The second approach uses a state-of-the-art neural network to estimate the distortion parameters rather than sampling them from a set of potential values. Extensive experiments on multiple datasets, and different camera setups, show that complex minimal radial distortion solvers are not necessary in practice. We discuss under which conditions a simple sampling of radial undistortion parameters is preferable over calibrating cameras using a learning-based prior approach. Code and newly created benchmark for relative pose estimation under radial distortion are available at https://github.com/kocurvik/rdnet.

A Guide to Structureless Visual Localization

Visual localization algorithms, i.e., methods that estimate the camera pose of a query image in a known scene, are core components of many applications, including self-driving cars and augmented / mixed reality systems. State-of-the-art visual localization algorithms are structure-based, i.e., they store a 3D model of the scene and use 2D-3D correspondences between the query image and 3D points in the model for camera pose estimation. While such approaches are highly accurate, they are also rather inflexible when it comes to adjusting the underlying 3D model after changes in the scene. Structureless localization approaches represent the scene as a database of images with known poses and thus offer a much more flexible representation that can be easily updated by adding or removing images. Although there is a large amount of literature on structure-based approaches, there is significantly less work on structureless methods. Hence, this paper is dedicated to providing the, to the best of our knowledge, first comprehensive discussion and comparison of structureless methods. Extensive experiments show that approaches that use a higher degree of classical geometric reasoning generally achieve higher pose accuracy. In particular, approaches based on classical absolute or semi-generalized relative pose estimation outperform very recent methods based on pose regression by a wide margin. Compared with state-of-the-art structure-based approaches, the flexibility of structureless methods comes at the cost of (slightly) lower pose accuracy, indicating an interesting direction for future work.

Diff-Reg v2: Diffusion-Based Matching Matrix Estimation for Image Matching and 3D Registration

Establishing reliable correspondences is crucial for all registration tasks, including 2D image registration, 3D point cloud registration, and 2D-3D image-to-point cloud registration. However, these tasks are often complicated by challenges such as scale inconsistencies, symmetry, and large deformations, which can lead to ambiguous matches. Previous feature-based and correspondence-based methods typically rely on geometric or semantic features to generate or polish initial potential correspondences. Some methods typically leverage specific geometric priors, such as topological preservation, to devise diverse and innovative strategies tailored to a given enhancement goal, which cannot be exhaustively enumerated. Additionally, many previous approaches rely on a single-step prediction head, which can struggle with local minima in complex matching scenarios. To address these challenges, we introduce an innovative paradigm that leverages a diffusion model in matrix space for robust matching matrix estimation. Our model treats correspondence estimation as a denoising diffusion process in the matching matrix space, gradually refining the intermediate matching matrix to the optimal one. Specifically, we apply the diffusion model in the doubly stochastic matrix space for 3D-3D and 2D-3D registration tasks. In the 2D image registration task, we deploy the diffusion model in a matrix subspace where dual-softmax projection regularization is applied. For all three registration tasks, we provide adaptive matching matrix embedding implementations tailored to the specific characteristics of each task while maintaining a consistent "match-to-warp" encoding pattern. Furthermore, we adopt a lightweight design for the denoising module. In inference, once points or image features are extracted and fixed, this module performs multi-step denoising predictions through reverse sampling.

Three-view Focal Length Recovery From Homographies

In this paper, we propose a novel approach for recovering focal lengths from three-view homographies. By examining the consistency of normal vectors between two homographies, we derive new explicit constraints between the focal lengths and homographies using an elimination technique. We demonstrate that three-view homographies provide two additional constraints, enabling the recovery of one or two focal lengths. We discuss four possible cases, including three cameras having an unknown equal focal length, three cameras having two different unknown focal lengths, three cameras where one focal length is known, and the other two cameras have equal or different unknown focal lengths. All the problems can be converted into solving polynomials in one or two unknowns, which can be efficiently solved using Sturm sequence or hidden variable technique. Evaluation using both synthetic and real data shows that the proposed solvers are both faster and more accurate than methods relying on existing two-view solvers. The code and data are available on https://github.com/kocurvik/hf

Fixing the Scale and Shift in Monocular Depth For Camera Pose Estimation

Recent advances in monocular depth prediction have led to significantly improved depth prediction accuracy. In turn, this enables various applications to use such depth predictions. In this paper, we propose a novel framework for estimating the relative pose between two cameras from point correspondences with associated monocular depths. Since depth predictions are typically defined up to an unknown scale and shift parameter, our solvers jointly estimate both scale and shift parameters together with the camera pose. We derive efficient solvers for three cases: (1) two calibrated cameras, (2) two uncalibrated cameras with an unknown but shared focal length, and (3) two uncalibrated cameras with unknown and different focal lengths. Experiments on synthetic and real data, including experiments with depth maps estimated by 11 different depth predictors, show the practical viability of our solvers. Compared to prior work, our solvers achieve state-of-the-art results on two large-scale, real-world datasets. The source code is available at https://github.com/yaqding/pose_monodepth

Are Minimal Radial Distortion Solvers Necessary for Relative Pose Estimation?

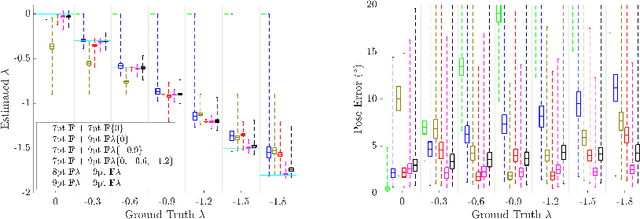
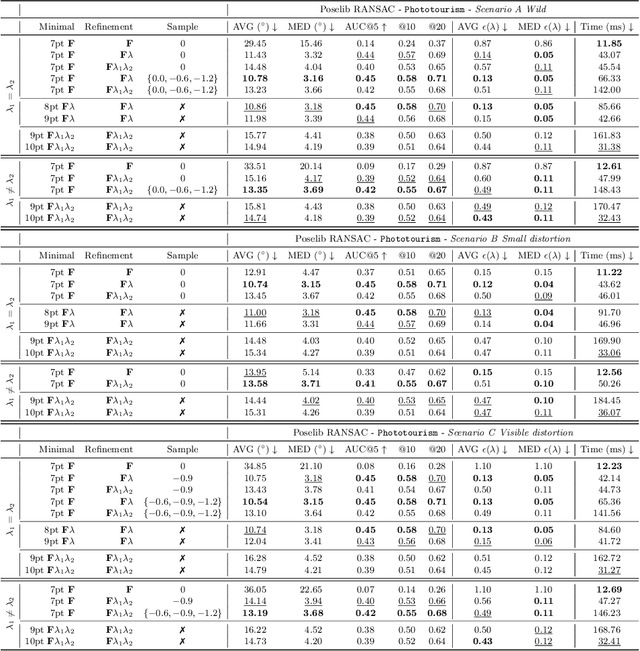
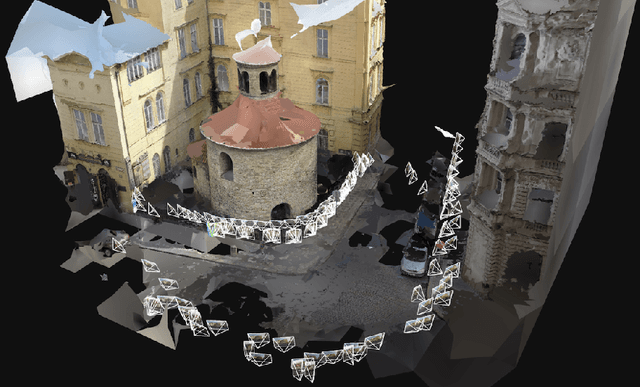
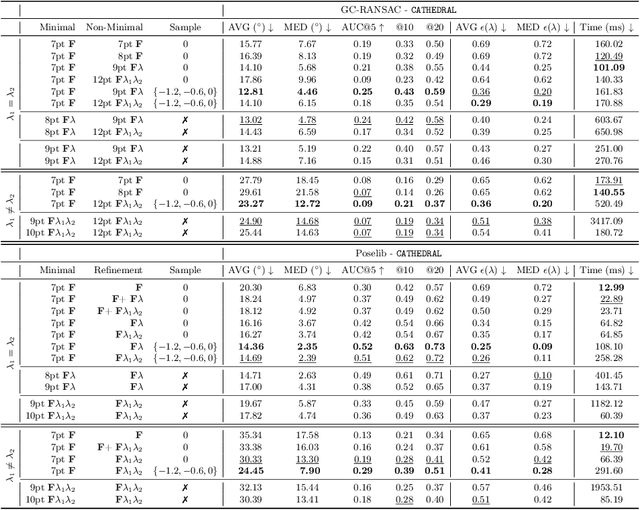
Estimating the relative pose between two cameras is a fundamental step in many applications such as Structure-from-Motion. The common approach to relative pose estimation is to apply a minimal solver inside a RANSAC loop. Highly efficient solvers exist for pinhole cameras. Yet, (nearly) all cameras exhibit radial distortion. Not modeling radial distortion leads to (significantly) worse results. However, minimal radial distortion solvers are significantly more complex than pinhole solvers, both in terms of run-time and implementation efforts. This paper compares radial distortion solvers with a simple-to-implement approach that combines an efficient pinhole solver with sampled radial distortion parameters. Extensive experiments on multiple datasets and RANSAC variants show that this simple approach performs similarly or better than the most accurate minimal distortion solvers at faster run-times while being significantly more accurate than faster non-minimal solvers. We clearly show that complex radial distortion solvers are not necessary in practice. Code and benchmark are available at https://github.com/kocurvik/rd.

Diff-Reg v1: Diffusion Matching Model for Registration Problem

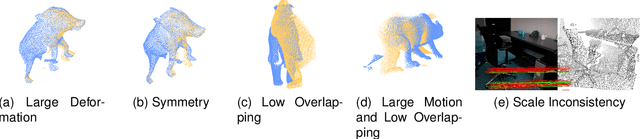
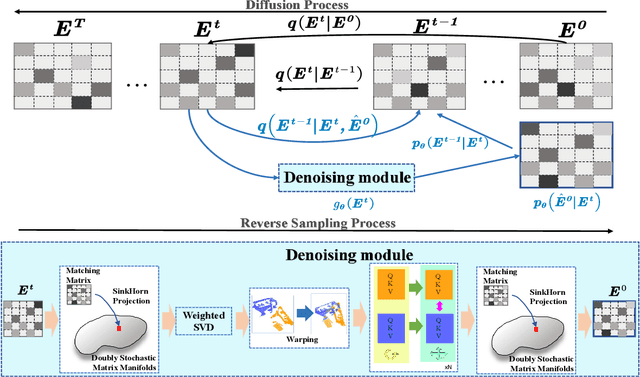
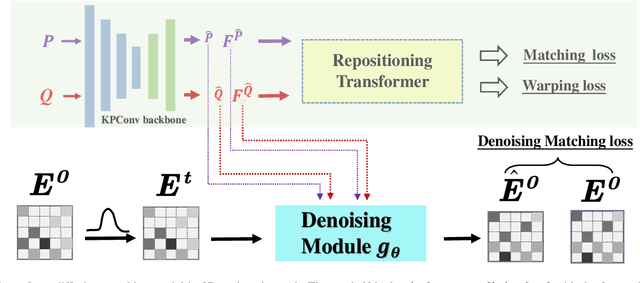
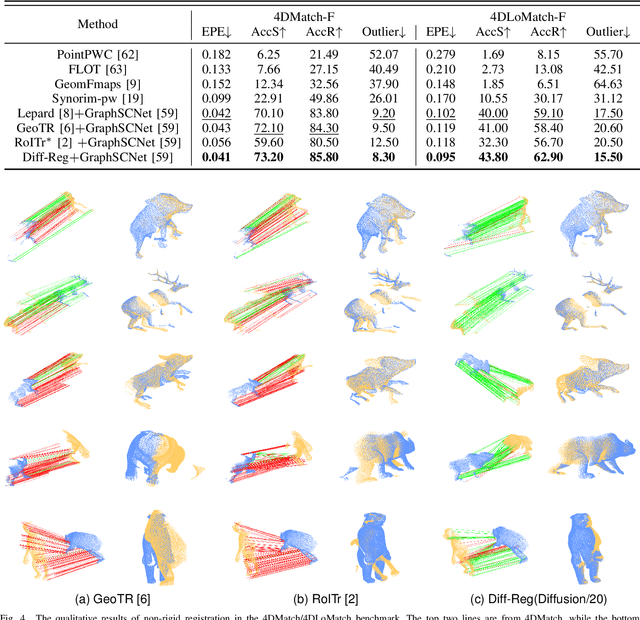
Establishing reliable correspondences is essential for registration tasks such as 3D and 2D3D registration. Existing methods commonly leverage geometric or semantic point features to generate potential correspondences. However, these features may face challenges such as large deformation, scale inconsistency, and ambiguous matching problems (e.g., symmetry). Additionally, many previous methods, which rely on single-pass prediction, may struggle with local minima in complex scenarios. To mitigate these challenges, we introduce a diffusion matching model for robust correspondence construction. Our approach treats correspondence estimation as a denoising diffusion process within the doubly stochastic matrix space, which gradually denoises (refines) a doubly stochastic matching matrix to the ground-truth one for high-quality correspondence estimation. It involves a forward diffusion process that gradually introduces Gaussian noise into the ground truth matching matrix and a reverse denoising process that iteratively refines the noisy matching matrix. In particular, the feature extraction from the backbone occurs only once during the inference phase. Our lightweight denoising module utilizes the same feature at each reverse sampling step. Evaluation of our method on both 3D and 2D3D registration tasks confirms its effectiveness.

Diff-PCR: Diffusion-Based Correspondence Searching in Doubly Stochastic Matrix Space for Point Cloud Registration

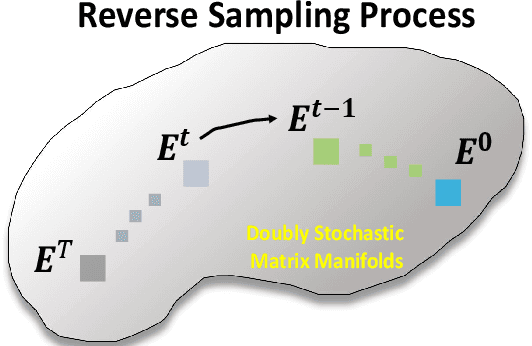
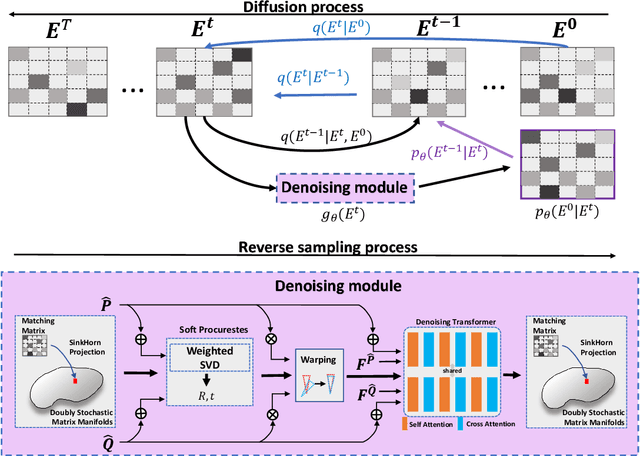
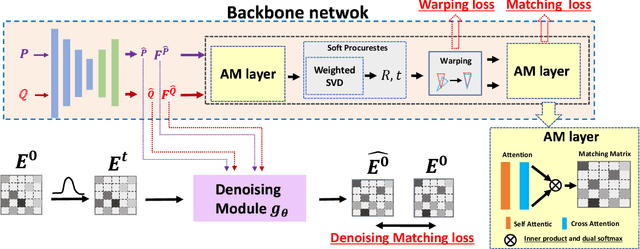
Efficiently finding optimal correspondences between point clouds is crucial for solving both rigid and non-rigid point cloud registration problems. Existing methods often rely on geometric or semantic feature embedding to establish correspondences and estimate transformations or flow fields. Recently, state-of-the-art methods have employed RAFT-like iterative updates to refine the solution. However, these methods have certain limitations. Firstly, their iterative refinement design lacks transparency, and their iterative updates follow a fixed path during the refinement process, which can lead to suboptimal results. Secondly, these methods overlook the importance of refining or optimizing correspondences (or matching matrices) as a precursor to solving transformations or flow fields. They typically compute candidate correspondences based on distances in the point feature space. However, they only project the candidate matching matrix into some matrix space once with Sinkhorn or dual softmax operations to obtain final correspondences. This one-shot projected matching matrix may be far from the globally optimal one, and these approaches do not consider the distribution of the target matching matrix. In this paper, we propose a novel approach that exploits the Denoising Diffusion Model to predict a searching gradient for the optimal matching matrix within the Doubly Stochastic Matrix Space. During the reverse denoising process, our method iteratively searches for better solutions along this denoising gradient, which points towards the maximum likelihood direction of the target matching matrix. Our method offers flexibility by allowing the search to start from any initial matching matrix provided by the online backbone or white noise. Experimental evaluations on the 3DMatch/3DLoMatch and 4DMatch/4DLoMatch datasets demonstrate the effectiveness of our newly designed framework.

SGFeat: Salient Geometric Feature for Point Cloud Registration

Point Cloud Registration (PCR) is a critical and challenging task in computer vision. One of the primary difficulties in PCR is identifying salient and meaningful points that exhibit consistent semantic and geometric properties across different scans. Previous methods have encountered challenges with ambiguous matching due to the similarity among patch blocks throughout the entire point cloud and the lack of consideration for efficient global geometric consistency. To address these issues, we propose a new framework that includes several novel techniques. Firstly, we introduce a semantic-aware geometric encoder that combines object-level and patch-level semantic information. This encoder significantly improves registration recall by reducing ambiguity in patch-level superpoint matching. Additionally, we incorporate a prior knowledge approach that utilizes an intrinsic shape signature to identify salient points. This enables us to extract the most salient super points and meaningful dense points in the scene. Secondly, we introduce an innovative transformer that encodes High-Order (HO) geometric features. These features are crucial for identifying salient points within initial overlap regions while considering global high-order geometric consistency. To optimize this high-order transformer further, we introduce an anchor node selection strategy. By encoding inter-frame triangle or polyhedron consistency features based on these anchor nodes, we can effectively learn high-order geometric features of salient super points. These high-order features are then propagated to dense points and utilized by a Sinkhorn matching module to identify key correspondences for successful registration. In our experiments conducted on well-known datasets such as 3DMatch/3DLoMatch and KITTI, our approach has shown promising results, highlighting the effectiveness of our novel method.