Light3R-SfM: Towards Feed-forward Structure-from-Motion

We present Light3R-SfM, a feed-forward, end-to-end learnable framework for efficient large-scale Structure-from-Motion (SfM) from unconstrained image collections. Unlike existing SfM solutions that rely on costly matching and global optimization to achieve accurate 3D reconstructions, Light3R-SfM addresses this limitation through a novel latent global alignment module. This module replaces traditional global optimization with a learnable attention mechanism, effectively capturing multi-view constraints across images for robust and precise camera pose estimation. Light3R-SfM constructs a sparse scene graph via retrieval-score-guided shortest path tree to dramatically reduce memory usage and computational overhead compared to the naive approach. Extensive experiments demonstrate that Light3R-SfM achieves competitive accuracy while significantly reducing runtime, making it ideal for 3D reconstruction tasks in real-world applications with a runtime constraint. This work pioneers a data-driven, feed-forward SfM approach, paving the way toward scalable, accurate, and efficient 3D reconstruction in the wild.

(Just) A Spoonful of Refinements Helps the Registration Error Go Down

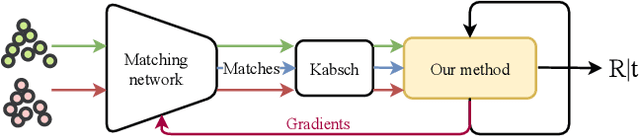
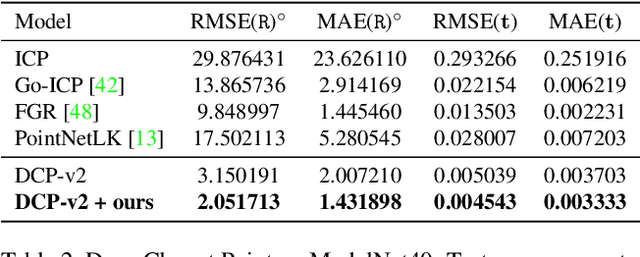
We tackle data-driven 3D point cloud registration. Given point correspondences, the standard Kabsch algorithm provides an optimal rotation estimate. This allows to train registration models in an end-to-end manner by differentiating the SVD operation. However, given the initial rotation estimate supplied by Kabsch, we show we can improve point correspondence learning during model training by extending the original optimization problem. In particular, we linearize the governing constraints of the rotation matrix and solve the resulting linear system of equations. We then iteratively produce new solutions by updating the initial estimate. Our experiments show that, by plugging our differentiable layer to existing learning-based registration methods, we improve the correspondence matching quality. This yields up to a 7% decrease in rotation error for correspondence-based data-driven registration methods.

CvxPnPL: A Unified Convex Solution to the Absolute Pose Estimation Problem from Point and Line Correspondences

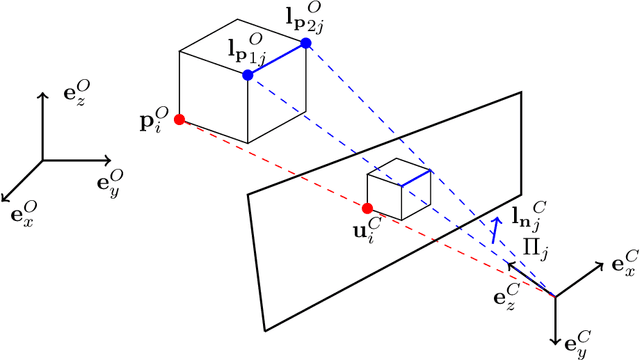
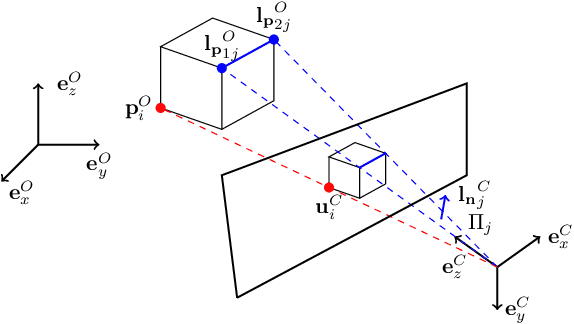
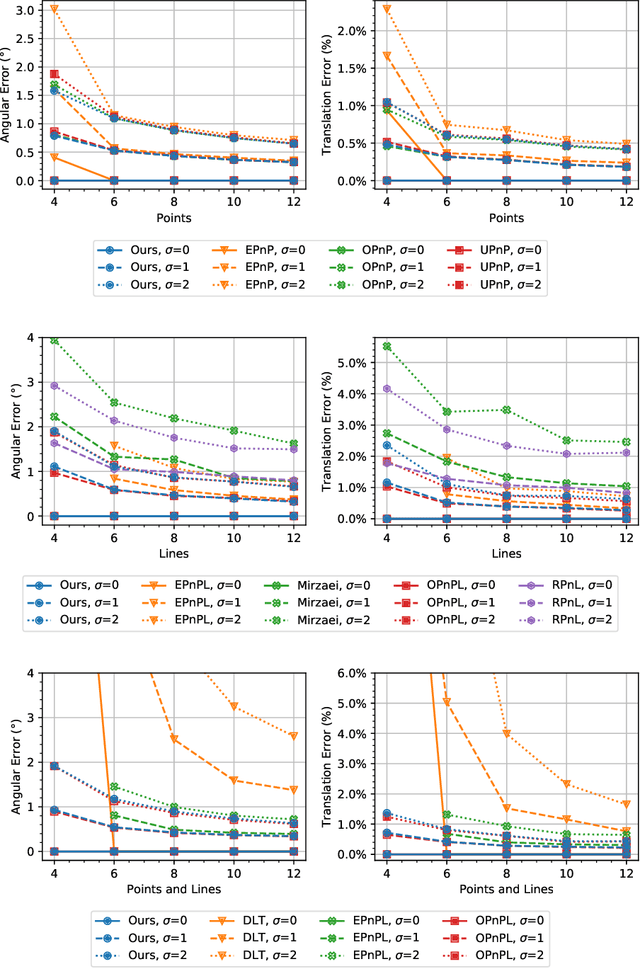
We present a new convex method to estimate 3D pose from mixed combinations of 2D-3D point and line correspondences, the Perspective-n-Points-and-Lines problem (PnPL). We merge the contributions of each point and line into a unified Quadratic Constrained Quadratic Problem (QCQP) and then relax it into a Semi Definite Program (SDP) through Shor's relaxation. This makes it possible to gracefully handle mixed configurations of points and lines. Furthermore, the proposed relaxation allows us to recover a finite number of solutions under ambiguous configurations. In such cases, the 3D pose candidates are found by further enforcing geometric constraints on the solution space and then retrieving such poses from the intersections of multiple quadrics. Experiments provide results in line with the best performing state of the art methods while providing the flexibility of solving for an arbitrary number of points and lines.