CvxPnPL: A Unified Convex Solution to the Absolute Pose Estimation Problem from Point and Line Correspondences
Paper and Code
Aug 09, 2019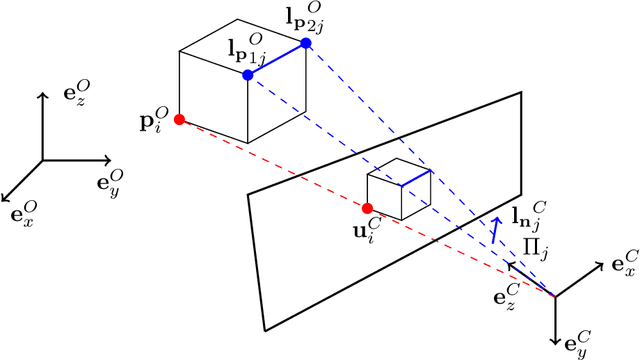
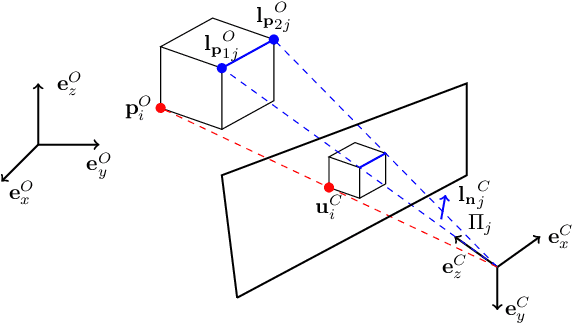

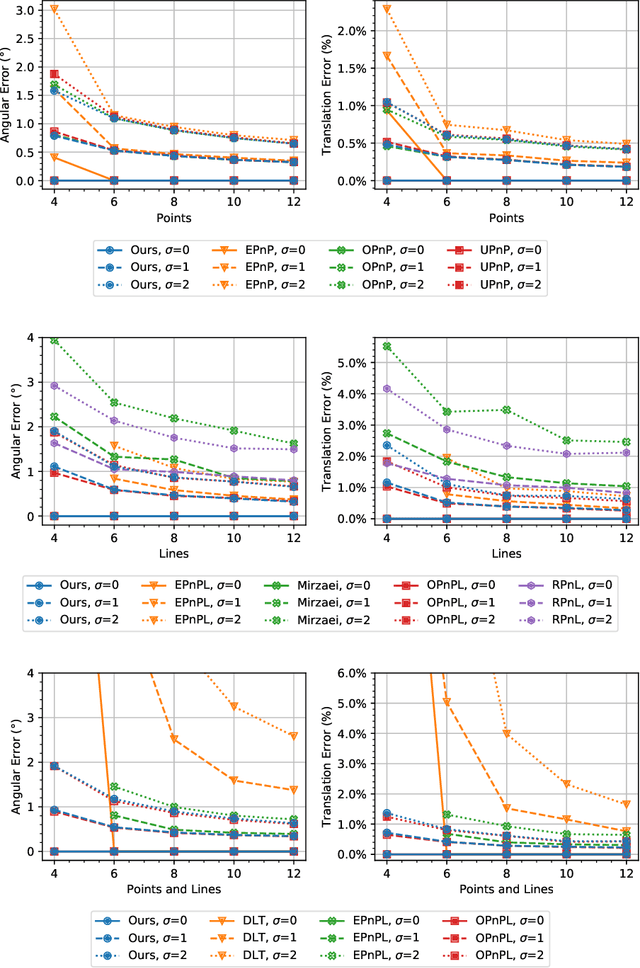
We present a new convex method to estimate 3D pose from mixed combinations of 2D-3D point and line correspondences, the Perspective-n-Points-and-Lines problem (PnPL). We merge the contributions of each point and line into a unified Quadratic Constrained Quadratic Problem (QCQP) and then relax it into a Semi Definite Program (SDP) through Shor's relaxation. This makes it possible to gracefully handle mixed configurations of points and lines. Furthermore, the proposed relaxation allows us to recover a finite number of solutions under ambiguous configurations. In such cases, the 3D pose candidates are found by further enforcing geometric constraints on the solution space and then retrieving such poses from the intersections of multiple quadrics. Experiments provide results in line with the best performing state of the art methods while providing the flexibility of solving for an arbitrary number of points and lines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge