EquiBind: Geometric Deep Learning for Drug Binding Structure Prediction

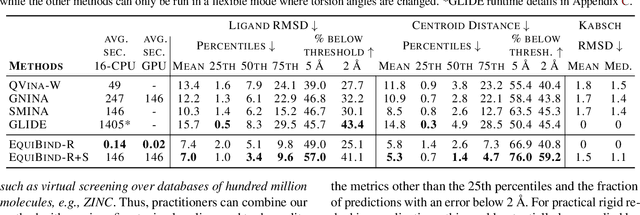
Predicting how a drug-like molecule binds to a specific protein target is a core problem in drug discovery. An extremely fast computational binding method would enable key applications such as fast virtual screening or drug engineering. Existing methods are computationally expensive as they rely on heavy candidate sampling coupled with scoring, ranking, and fine-tuning steps. We challenge this paradigm with EquiBind, an SE(3)-equivariant geometric deep learning model performing direct-shot prediction of both i) the receptor binding location (blind docking) and ii) the ligand's bound pose and orientation. EquiBind achieves significant speed-ups and better quality compared to traditional and recent baselines. Further, we show extra improvements when coupling it with existing fine-tuning techniques at the cost of increased running time. Finally, we propose a novel and fast fine-tuning model that adjusts torsion angles of a ligand's rotatable bonds based on closed-form global minima of the von Mises angular distance to a given input atomic point cloud, avoiding previous expensive differential evolution strategies for energy minimization.

Independent SE-Equivariant Models for End-to-End Rigid Protein Docking

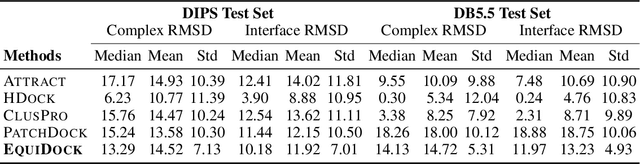
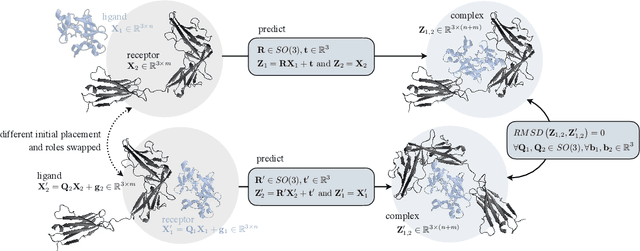
Protein complex formation is a central problem in biology, being involved in most of the cell's processes, and essential for applications, e.g. drug design or protein engineering. We tackle rigid body protein-protein docking, i.e., computationally predicting the 3D structure of a protein-protein complex from the individual unbound structures, assuming no conformational change within the proteins happens during binding. We design a novel pairwise-independent SE(3)-equivariant graph matching network to predict the rotation and translation to place one of the proteins at the right docked position relative to the second protein. We mathematically guarantee a basic principle: the predicted complex is always identical regardless of the initial locations and orientations of the two structures. Our model, named EquiDock, approximates the binding pockets and predicts the docking poses using keypoint matching and alignment, achieved through optimal transport and a differentiable Kabsch algorithm. Empirically, we achieve significant running time improvements and often outperform existing docking software despite not relying on heavy candidate sampling, structure refinement, or templates.

Crystal Diffusion Variational Autoencoder for Periodic Material Generation

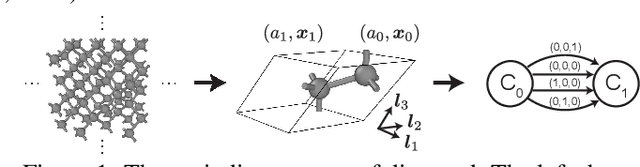
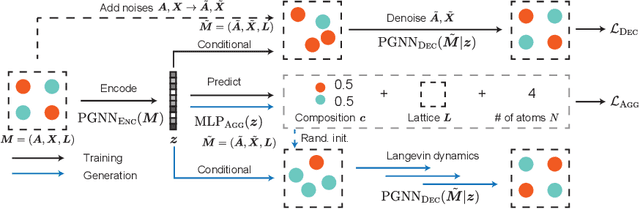
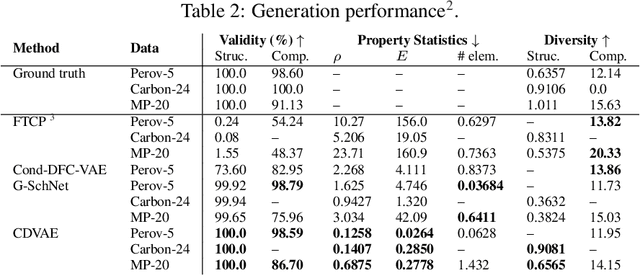
Generating the periodic structure of stable materials is a long-standing challenge for the material design community. This task is difficult because stable materials only exist in a low-dimensional subspace of all possible periodic arrangements of atoms: 1) the coordinates must lie in the local energy minimum defined by quantum mechanics, and 2) global stability also requires the structure to follow the complex, yet specific bonding preferences between different atom types. Existing methods fail to incorporate these factors and often lack proper invariances. We propose a Crystal Diffusion Variational Autoencoder (CDVAE) that captures the physical inductive bias of material stability. By learning from the data distribution of stable materials, the decoder generates materials in a diffusion process that moves atomic coordinates towards a lower energy state and updates atom types to satisfy bonding preferences between neighbors. Our model also explicitly encodes interactions across periodic boundaries and respects permutation, translation, rotation, and periodic invariances. We significantly outperform past methods in three tasks: 1) reconstructing the input structure, 2) generating valid, diverse, and realistic materials, and 3) generating materials that optimize a specific property. We also provide several standard datasets and evaluation metrics for the broader machine learning community.

GeoMol: Torsional Geometric Generation of Molecular 3D Conformer Ensembles

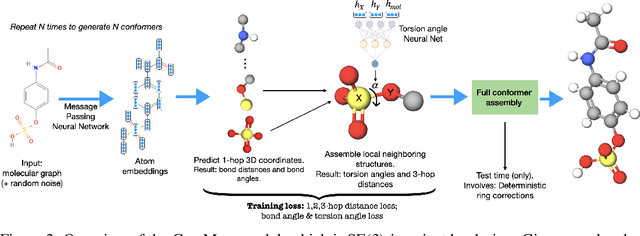
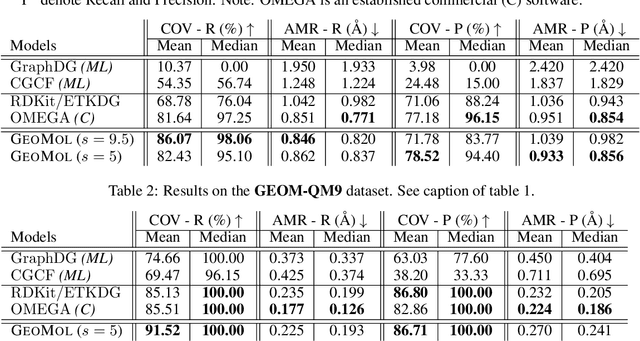
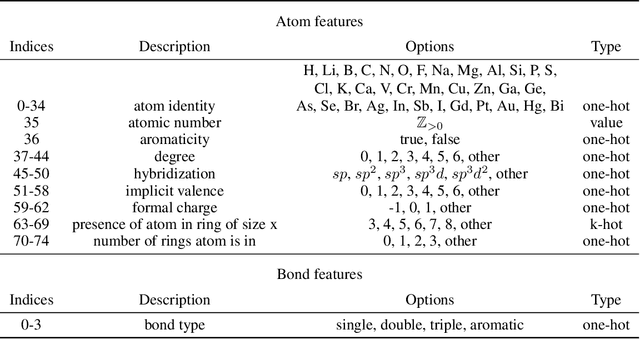
Prediction of a molecule's 3D conformer ensemble from the molecular graph holds a key role in areas of cheminformatics and drug discovery. Existing generative models have several drawbacks including lack of modeling important molecular geometry elements (e.g. torsion angles), separate optimization stages prone to error accumulation, and the need for structure fine-tuning based on approximate classical force-fields or computationally expensive methods such as metadynamics with approximate quantum mechanics calculations at each geometry. We propose GeoMol--an end-to-end, non-autoregressive and SE(3)-invariant machine learning approach to generate distributions of low-energy molecular 3D conformers. Leveraging the power of message passing neural networks (MPNNs) to capture local and global graph information, we predict local atomic 3D structures and torsion angles, avoiding unnecessary over-parameterization of the geometric degrees of freedom (e.g. one angle per non-terminal bond). Such local predictions suffice both for the training loss computation, as well as for the full deterministic conformer assembly (at test time). We devise a non-adversarial optimal transport based loss function to promote diverse conformer generation. GeoMol predominantly outperforms popular open-source, commercial, or state-of-the-art machine learning (ML) models, while achieving significant speed-ups. We expect such differentiable 3D structure generators to significantly impact molecular modeling and related applications.

Message Passing Networks for Molecules with Tetrahedral Chirality

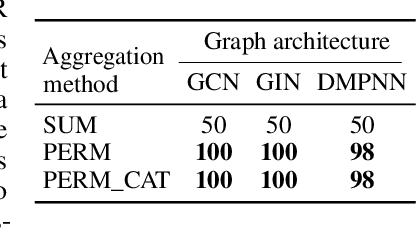
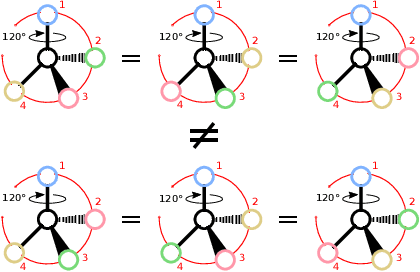
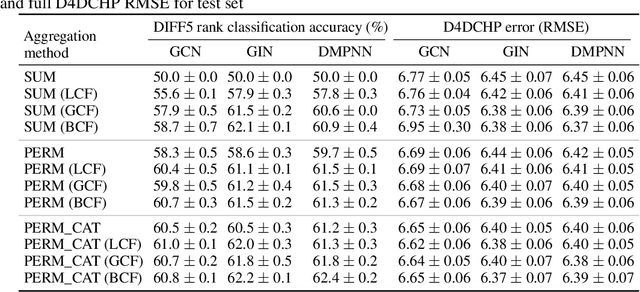
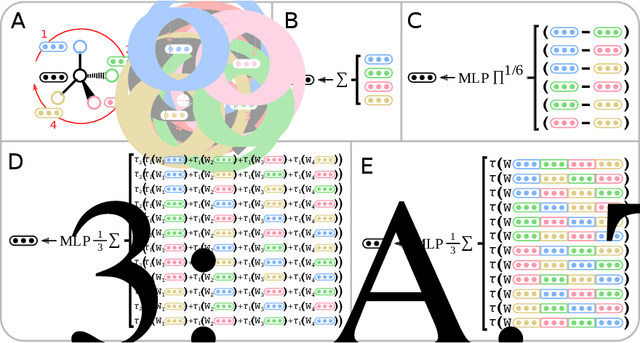
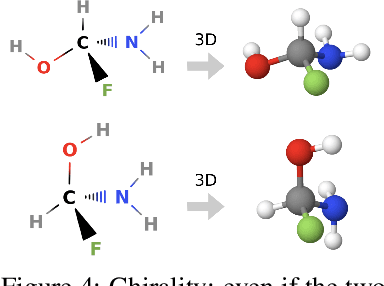
Molecules with identical graph connectivity can exhibit different physical and biological properties if they exhibit stereochemistry-a spatial structural characteristic. However, modern neural architectures designed for learning structure-property relationships from molecular structures treat molecules as graph-structured data and therefore are invariant to stereochemistry. Here, we develop two custom aggregation functions for message passing neural networks to learn properties of molecules with tetrahedral chirality, one common form of stereochemistry. We evaluate performance on synthetic data as well as a newly-proposed protein-ligand docking dataset with relevance to drug discovery. Results show modest improvements over a baseline sum aggregator, highlighting opportunities for further architecture development.

Optimal Transport Graph Neural Networks

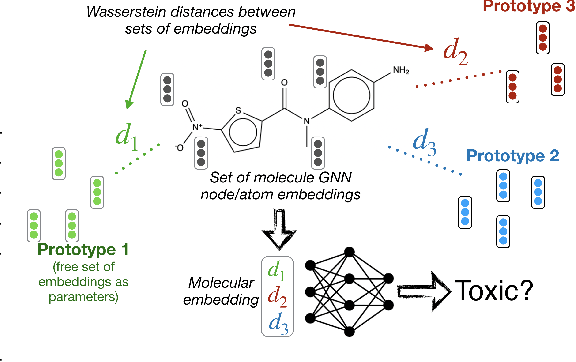
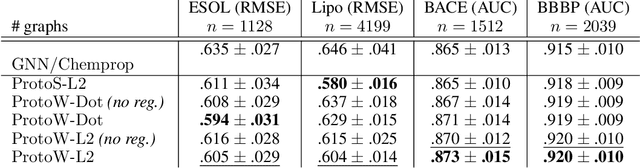
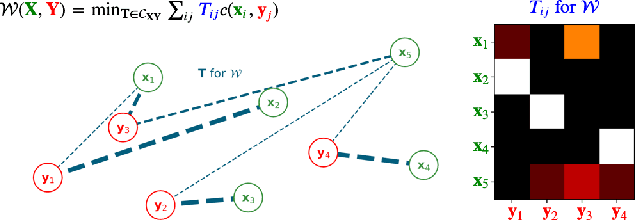
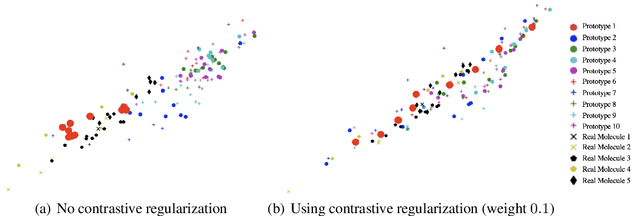
Current graph neural network (GNN) architectures naively average or sum node embeddings into an aggregated graph representation---potentially losing structural or semantic information. We here introduce OT-GNN that compute graph embeddings from optimal transport distances between the set of GNN node embeddings and "prototype" point clouds as free parameters. This allows different prototypes to highlight key facets of different graph subparts. We show that our function class on point clouds satisfies a universal approximation theorem, a fundamental property which was lost by sum aggregation. Nevertheless, empirically the model has a natural tendency to collapse back to the standard aggregation during training. We address this optimization issue by proposing an efficient noise contrastive regularizer, steering the model towards truly exploiting the optimal transport geometry. Our model consistently exhibits better generalization performance on several molecular property prediction tasks, yielding also smoother representations.

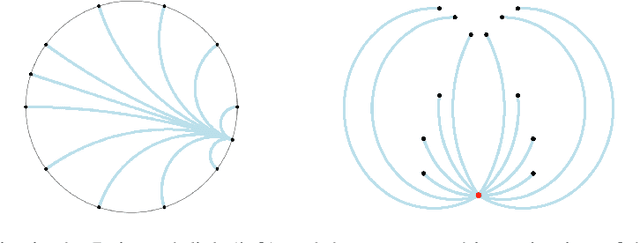
Computationally Tractable Riemannian Manifolds for Graph Embeddings

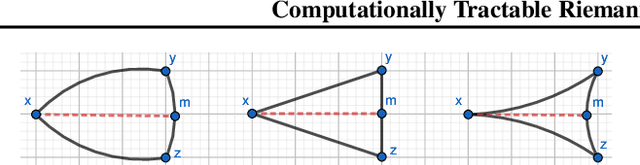
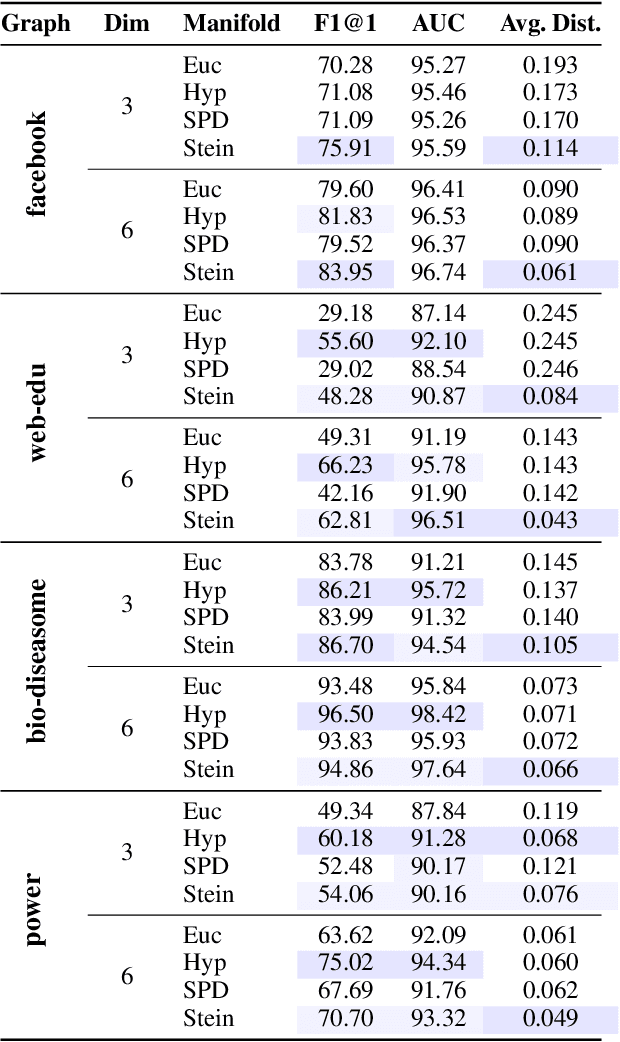
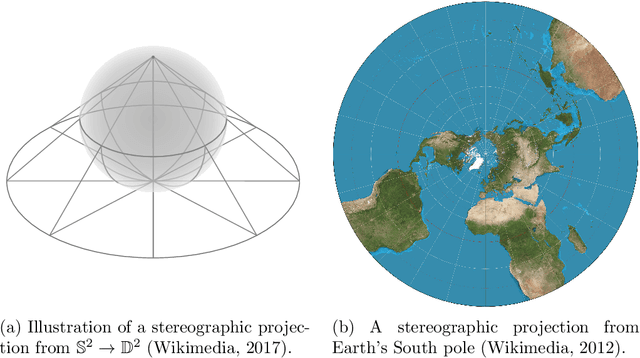
Representing graphs as sets of node embeddings in certain curved Riemannian manifolds has recently gained momentum in machine learning due to their desirable geometric inductive biases, e.g., hierarchical structures benefit from hyperbolic geometry. However, going beyond embedding spaces of constant sectional curvature, while potentially more representationally powerful, proves to be challenging as one can easily lose the appeal of computationally tractable tools such as geodesic distances or Riemannian gradients. Here, we explore computationally efficient matrix manifolds, showcasing how to learn and optimize graph embeddings in these Riemannian spaces. Empirically, we demonstrate consistent improvements over Euclidean geometry while often outperforming hyperbolic and elliptical embeddings based on various metrics that capture different graph properties. Our results serve as new evidence for the benefits of non-Euclidean embeddings in machine learning pipelines.

Mixed-curvature Variational Autoencoders

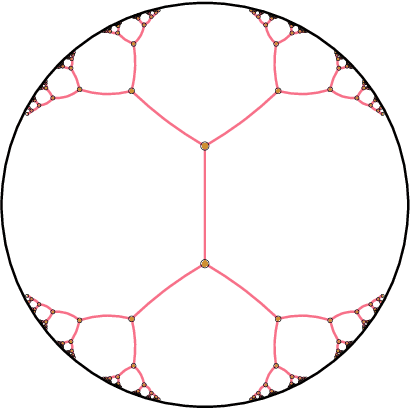
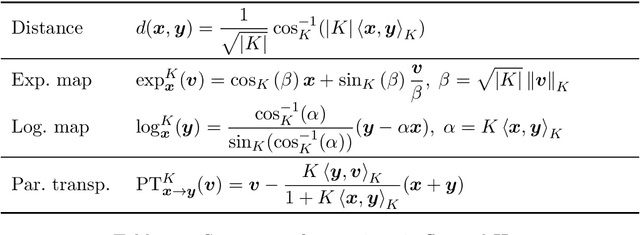
It has been shown that using geometric spaces with non-zero curvature instead of plain Euclidean spaces with zero curvature improves performance on a range of Machine Learning tasks for learning representations. Recent work has leveraged these geometries to learn latent variable models like Variational Autoencoders (VAEs) in spherical and hyperbolic spaces with constant curvature. While these approaches work well on particular kinds of data that they were designed for e.g. tree-like data for a hyperbolic VAE, there exists no generic approach unifying all three models. We develop a Mixed-curvature Variational Autoencoder, an efficient way to train a VAE whose latent space is a product of constant curvature Riemannian manifolds, where the per-component curvature can be learned. This generalizes the Euclidean VAE to curved latent spaces, as the model essentially reduces to the Euclidean VAE if curvatures of all latent space components go to 0.

Constant Curvature Graph Convolutional Networks

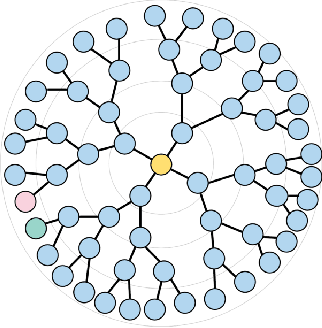
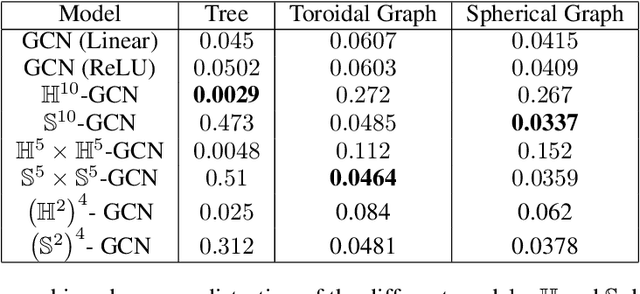
Interest has been rising lately towards methods representing data in non-Euclidean spaces, e.g. hyperbolic or spherical, that provide specific inductive biases useful for certain real-world data properties, e.g. scale-free, hierarchical or cyclical. However, the popular graph neural networks are currently limited in modeling data only via Euclidean geometry and associated vector space operations. Here, we bridge this gap by proposing mathematically grounded generalizations of graph convolutional networks (GCN) to (products of) constant curvature spaces. We do this by i) introducing a unified formalism that can interpolate smoothly between all geometries of constant curvature, ii) leveraging gyro-barycentric coordinates that generalize the classic Euclidean concept of the center of mass. Our class of models smoothly recover their Euclidean counterparts when the curvature goes to zero from either side. Empirically, we outperform Euclidean GCNs in the tasks of node classification and distortion minimization for symbolic data exhibiting non-Euclidean behavior, according to their discrete curvature.

Noise Contrastive Variational Autoencoders

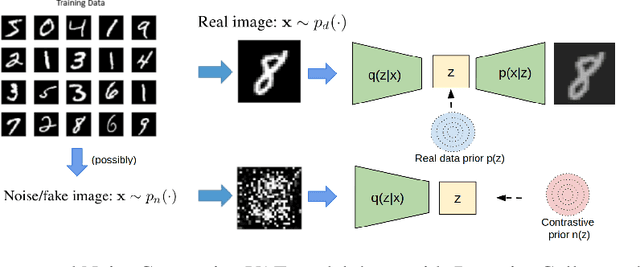
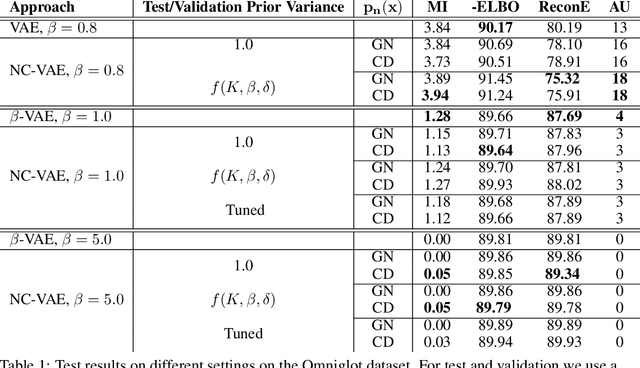
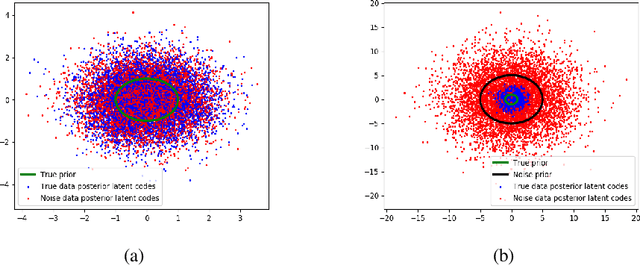
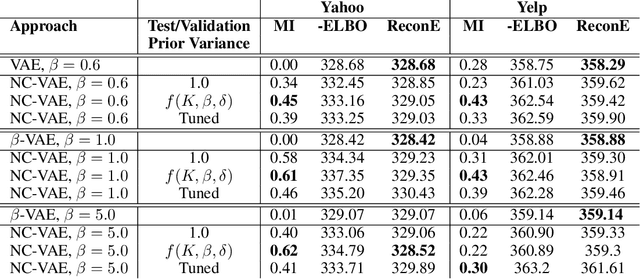
We take steps towards understanding the "posterior collapse (PC)" difficulty in variational autoencoders (VAEs),~i.e. a degenerate optimum in which the latent codes become independent of their corresponding inputs. We rely on calculus of variations and theoretically explore a few popular VAE models, showing that PC always occurs for non-parametric encoders and decoders. Inspired by the popular noise contrastive estimation algorithm, we propose NC-VAE where the encoder discriminates between the latent codes of real data and of some artificially generated noise, in addition to encouraging good data reconstruction abilities. Theoretically, we prove that our model cannot reach PC and provide novel lower bounds. Our method is straightforward to implement and has the same run-time as vanilla VAE. Empirically, we showcase its benefits on popular image and text datasets.