Mixed-curvature Variational Autoencoders

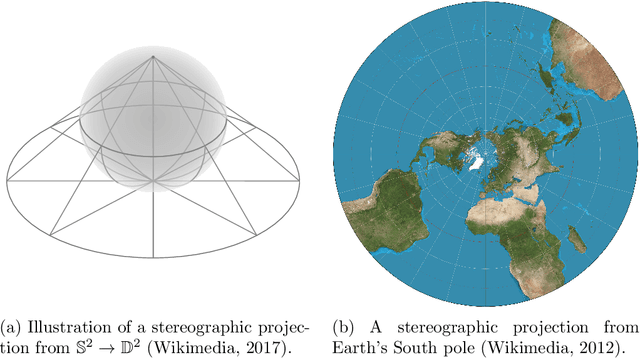
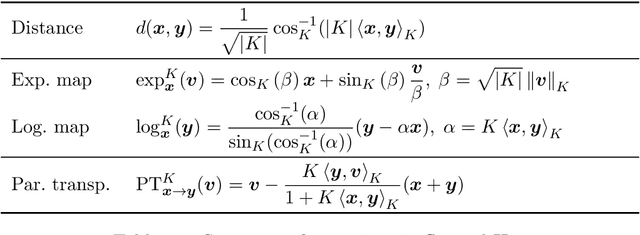
It has been shown that using geometric spaces with non-zero curvature instead of plain Euclidean spaces with zero curvature improves performance on a range of Machine Learning tasks for learning representations. Recent work has leveraged these geometries to learn latent variable models like Variational Autoencoders (VAEs) in spherical and hyperbolic spaces with constant curvature. While these approaches work well on particular kinds of data that they were designed for e.g. tree-like data for a hyperbolic VAE, there exists no generic approach unifying all three models. We develop a Mixed-curvature Variational Autoencoder, an efficient way to train a VAE whose latent space is a product of constant curvature Riemannian manifolds, where the per-component curvature can be learned. This generalizes the Euclidean VAE to curved latent spaces, as the model essentially reduces to the Euclidean VAE if curvatures of all latent space components go to 0.