Explicit Word Density Estimation for Language Modelling

Language Modelling has been a central part of Natural Language Processing for a very long time and in the past few years LSTM-based language models have been the go-to method for commercial language modeling. Recently, it has been shown that when looking at language modelling from a matrix factorization point of view, the final Softmax layer limits the expressiveness of the model, by putting an upper bound on the rank of the resulting matrix. Additionally, a new family of neural networks based called NeuralODEs, has been introduced as a continuous alternative to Residual Networks. Moreover, it has been shown that there is a connection between these models and Normalizing Flows. In this work we propose a new family of language models based on NeuralODEs and the continuous analogue of Normalizing Flows and manage to improve on some of the baselines.

Optimal Transport Graph Neural Networks

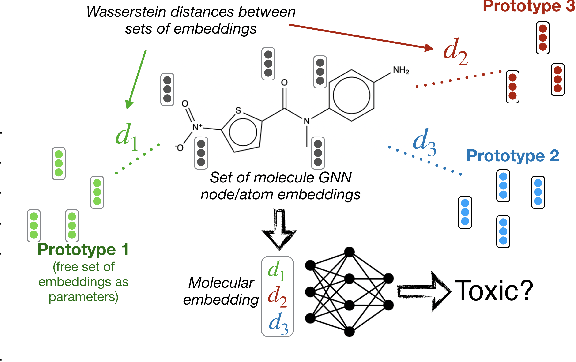
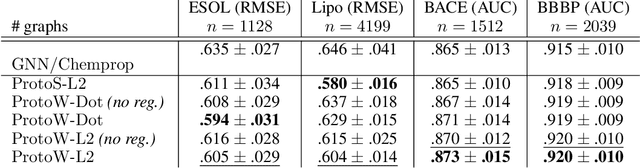
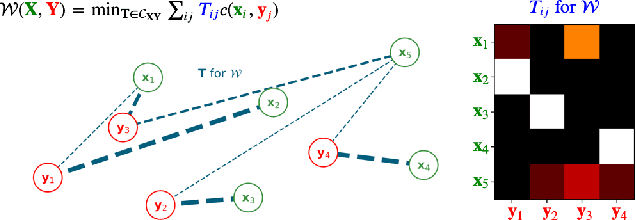
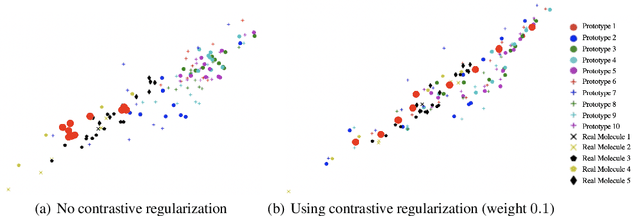
Current graph neural network (GNN) architectures naively average or sum node embeddings into an aggregated graph representation---potentially losing structural or semantic information. We here introduce OT-GNN that compute graph embeddings from optimal transport distances between the set of GNN node embeddings and "prototype" point clouds as free parameters. This allows different prototypes to highlight key facets of different graph subparts. We show that our function class on point clouds satisfies a universal approximation theorem, a fundamental property which was lost by sum aggregation. Nevertheless, empirically the model has a natural tendency to collapse back to the standard aggregation during training. We address this optimization issue by proposing an efficient noise contrastive regularizer, steering the model towards truly exploiting the optimal transport geometry. Our model consistently exhibits better generalization performance on several molecular property prediction tasks, yielding also smoother representations.

Crackovid: Optimizing Group Testing

We study the problem usually referred to as group testing in the context of COVID-19. Given $n$ samples taken from patients, how should we select mixtures of samples to be tested, so as to maximize information and minimize the number of tests? We consider both adaptive and non-adaptive strategies, and take a Bayesian approach with a prior both for infection of patients and test errors. We start by proposing a mathematically principled objective, grounded in information theory. We then optimize non-adaptive optimization strategies using genetic algorithms, and leverage the mathematical framework of adaptive sub-modularity to obtain theoretical guarantees for the greedy-adaptive method.

Computationally Tractable Riemannian Manifolds for Graph Embeddings

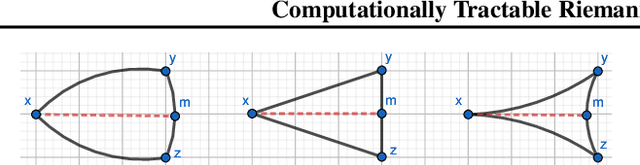
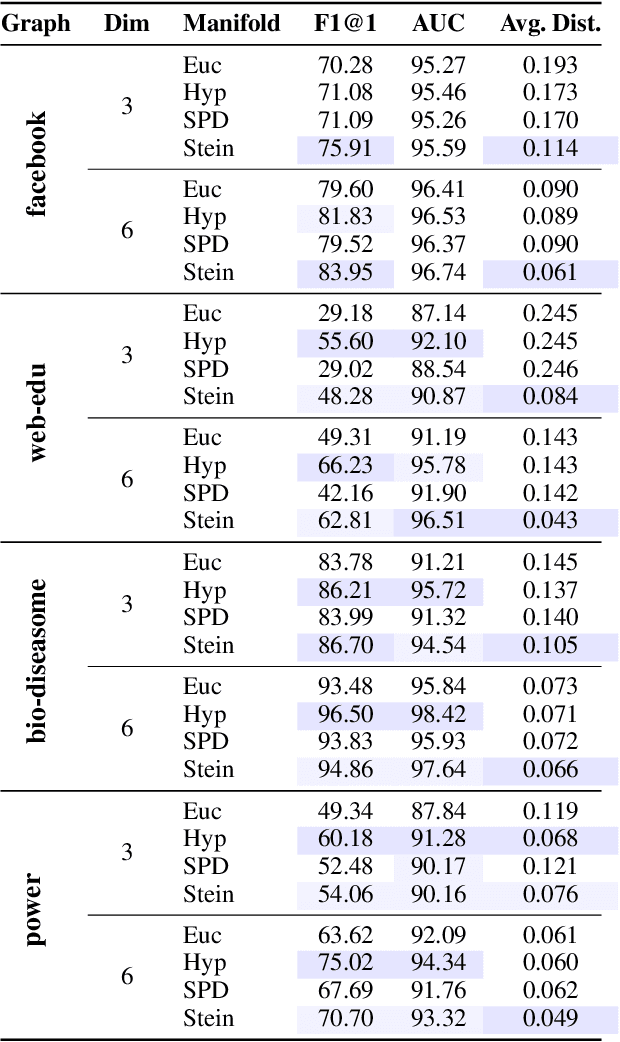
Representing graphs as sets of node embeddings in certain curved Riemannian manifolds has recently gained momentum in machine learning due to their desirable geometric inductive biases, e.g., hierarchical structures benefit from hyperbolic geometry. However, going beyond embedding spaces of constant sectional curvature, while potentially more representationally powerful, proves to be challenging as one can easily lose the appeal of computationally tractable tools such as geodesic distances or Riemannian gradients. Here, we explore computationally efficient matrix manifolds, showcasing how to learn and optimize graph embeddings in these Riemannian spaces. Empirically, we demonstrate consistent improvements over Euclidean geometry while often outperforming hyperbolic and elliptical embeddings based on various metrics that capture different graph properties. Our results serve as new evidence for the benefits of non-Euclidean embeddings in machine learning pipelines.

Mixed-curvature Variational Autoencoders

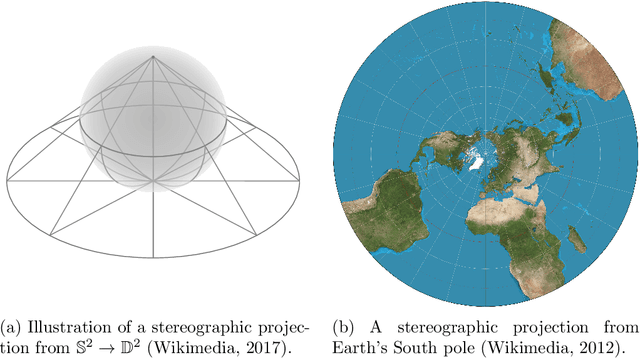
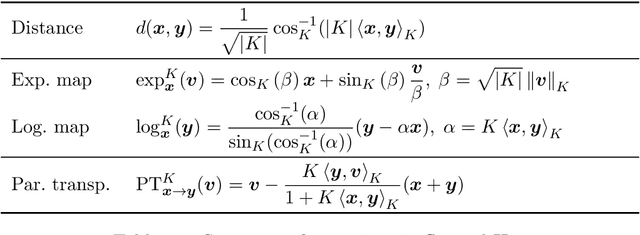
It has been shown that using geometric spaces with non-zero curvature instead of plain Euclidean spaces with zero curvature improves performance on a range of Machine Learning tasks for learning representations. Recent work has leveraged these geometries to learn latent variable models like Variational Autoencoders (VAEs) in spherical and hyperbolic spaces with constant curvature. While these approaches work well on particular kinds of data that they were designed for e.g. tree-like data for a hyperbolic VAE, there exists no generic approach unifying all three models. We develop a Mixed-curvature Variational Autoencoder, an efficient way to train a VAE whose latent space is a product of constant curvature Riemannian manifolds, where the per-component curvature can be learned. This generalizes the Euclidean VAE to curved latent spaces, as the model essentially reduces to the Euclidean VAE if curvatures of all latent space components go to 0.

Constant Curvature Graph Convolutional Networks

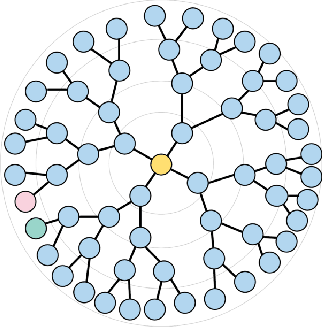
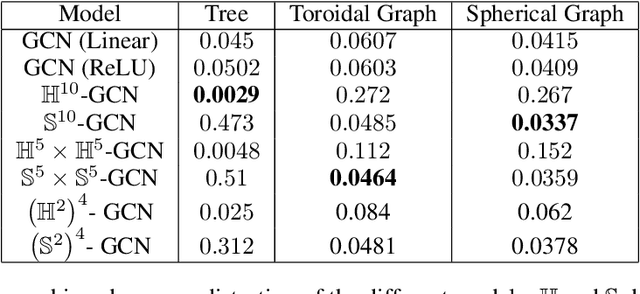
Interest has been rising lately towards methods representing data in non-Euclidean spaces, e.g. hyperbolic or spherical, that provide specific inductive biases useful for certain real-world data properties, e.g. scale-free, hierarchical or cyclical. However, the popular graph neural networks are currently limited in modeling data only via Euclidean geometry and associated vector space operations. Here, we bridge this gap by proposing mathematically grounded generalizations of graph convolutional networks (GCN) to (products of) constant curvature spaces. We do this by i) introducing a unified formalism that can interpolate smoothly between all geometries of constant curvature, ii) leveraging gyro-barycentric coordinates that generalize the classic Euclidean concept of the center of mass. Our class of models smoothly recover their Euclidean counterparts when the curvature goes to zero from either side. Empirically, we outperform Euclidean GCNs in the tasks of node classification and distortion minimization for symbolic data exhibiting non-Euclidean behavior, according to their discrete curvature.

Noise Contrastive Variational Autoencoders

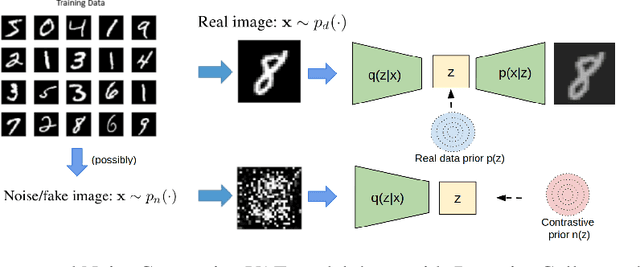
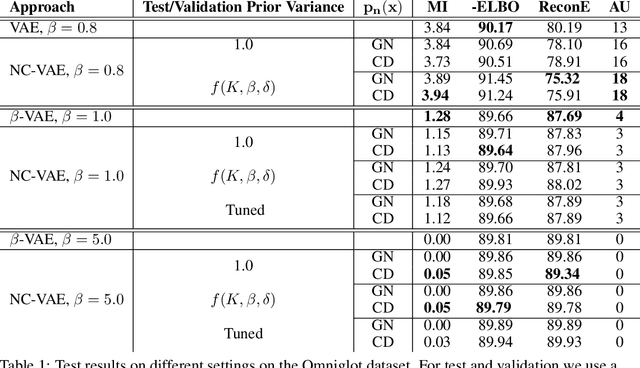
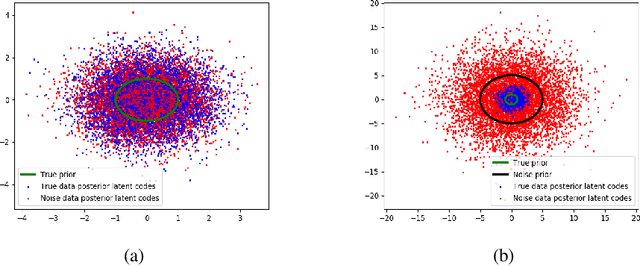
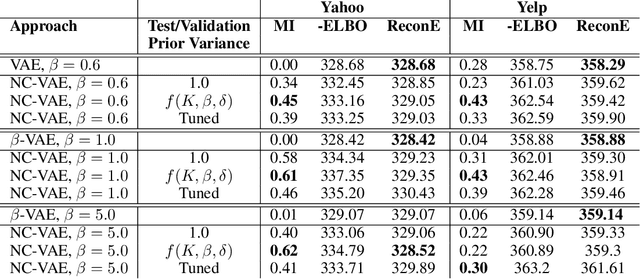
We take steps towards understanding the "posterior collapse (PC)" difficulty in variational autoencoders (VAEs),~i.e. a degenerate optimum in which the latent codes become independent of their corresponding inputs. We rely on calculus of variations and theoretically explore a few popular VAE models, showing that PC always occurs for non-parametric encoders and decoders. Inspired by the popular noise contrastive estimation algorithm, we propose NC-VAE where the encoder discriminates between the latent codes of real data and of some artificially generated noise, in addition to encouraging good data reconstruction abilities. Theoretically, we prove that our model cannot reach PC and provide novel lower bounds. Our method is straightforward to implement and has the same run-time as vanilla VAE. Empirically, we showcase its benefits on popular image and text datasets.

Breaking the Softmax Bottleneck via Learnable Monotonic Pointwise Non-linearities

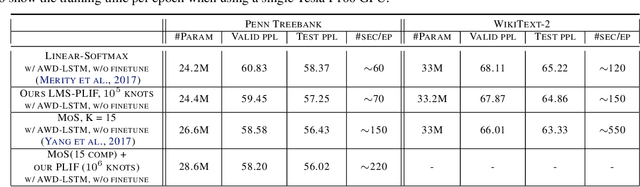
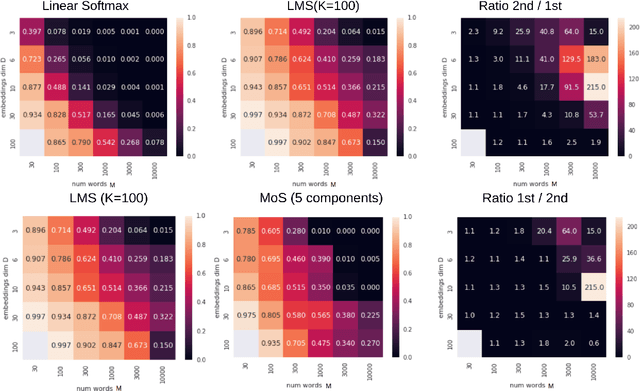
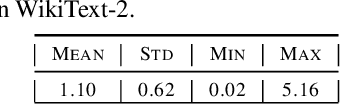
The softmax function on top of a final linear layer is the de facto method to output probability distributions in neural networks. In many applications such as language models or text generation, this model has to produce distributions over large output vocabularies. Recently, this has been shown to have limited representational capacity due to its connection with the rank bottleneck in matrix factorization. However, little is known about the limitations of linear-softmax for quantities of practical interest such as cross entropy or mode estimation, a direction that we theoretically and empirically explore here. As an efficient and effective solution to alleviate this issue, we propose to learn parametric monotonic functions on top of the logits. We theoretically investigate the rank increasing capabilities of such monotonic functions. Empirically, our method improves in two different quality metrics over the traditional softmax-linear layer in synthetic and real language model experiments, adding little time or memory overhead, while being comparable to the more computationally expensive mixture of softmaxes.

Poincaré GloVe: Hyperbolic Word Embeddings

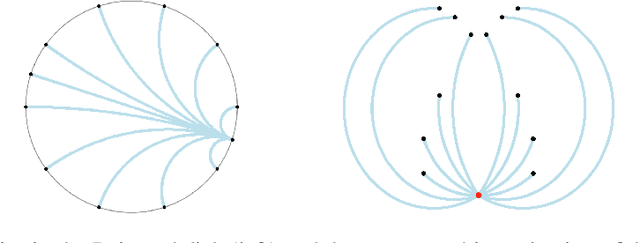
Words are not created equal. In fact, they form an aristocratic graph with a latent hierarchical structure that the next generation of unsupervised learned word embeddings should reveal. In this paper, driven by the notion of delta-hyperbolicity or tree-likeliness of a space, we propose to embed words in a Cartesian product of hyperbolic spaces which we theoretically connect with the Gaussian word embeddings and their Fisher distance. We adapt the well-known Glove algorithm to learn unsupervised word embeddings in this type of Riemannian manifolds. We explain how concepts from the Euclidean space such as parallel transport (used to solve analogy tasks) generalize to this new type of geometry. Moreover, we show that our embeddings exhibit hierarchical and hypernymy detection capabilities. We back up our findings with extensive experiments in which we outperform strong and popular baselines on the tasks of similarity, analogy and hypernymy detection.

Riemannian Adaptive Optimization Methods

Several first order stochastic optimization methods commonly used in the Euclidean domain such as stochastic gradient descent (SGD), accelerated gradient descent or variance reduced methods have already been adapted to certain Riemannian settings. However, some of the most popular of these optimization tools - namely Adam , Adagrad and the more recent Amsgrad - remain to be generalized to Riemannian manifolds. We discuss the difficulty of generalizing such adaptive schemes to the most agnostic Riemannian setting, and then provide algorithms and convergence proofs for geodesically convex objectives in the particular case of a product of Riemannian manifolds, in which adaptivity is implemented across manifolds in the cartesian product. Our generalization is tight in the sense that choosing the Euclidean space as Riemannian manifold yields the same algorithms and regret bounds as those that were already known for the standard algorithms. Experimentally, we show faster convergence and to a lower train loss value for Riemannian adaptive methods over their corresponding baselines on the realistic task of embedding the WordNet taxonomy in the Poincare ball.